Вопрос 36.Энтропия. Энтропия и законы термодинамики. Примеры вычисления энтропии.

- обратимый цикл; - необратимый цикл }=> интегралы Клазиуса и являются математической записью 2 Н т/д. Интегралы Клазиуса не зависят от того каким путем мы переводим систему из одного состояния в другое а выражениеδQ/T – является полным дифференциалом некоторой функции S являющийся функцией состояния. Эту функция назвали энтропией. Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты  полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т: dS=δQ/T. 1/T – интегральный множитель для δQ. [S]= Дж/К. Поскольку dS= δQ/T, a δQ – алгебраическая величина, то изменения энтропии dS зависит от того какой знак имеет δQ. δQ>0, dS>0 – энтропия возврастает, δQ<0 ,dS<0-убывает, δQ=0 – адиабатный процесс, то dS =0 – энтропия не изменяется. Энтропия обладает свойством аддитивности: энтропия всей системы состоит из нескольких частей равных сумме энтропийных частей этой системы. Если система изолирована и не получает тепло извне δQ=0, то S2-S1>0 - энтропия изолированной системы в которой протекают необратимые процессы возрастает. Изолированной назыв система окруженная жесткой адиабатной оболочкой (жесткой – не позволяет совершать работу над системой, адиабатной – препятствует охлаждению). Если в изолированной системе протекает только обратимые процессы то ,S=const – энтропия изолированной системы в которой протекает обратный процесс остается неизменный. Энтропия изолированной системы при любых процессах протекающих в ней не убывает. Поскольку все реальные процессы являются необратимыми то в изолированной системе они сопровождаются ростом энтропии. Энергия изолированной системы (И.С.) постоянная, то энтропия не может служить показателем того в каком направлении протекает процесс в этой системе. В конечном состоянии в И.С. энтропия всегда не меньше чем начальном. По изменению энтропии мы можем сказать в каком направлении протекает процесс. Энтропия возрастает до определенного значения. Закон возрастания энтропии в И.С.: энтропия И.С. стремится к максимуму. Примеры вычисления энтропии: 1 Н Т/Д: |=> |=>- обобщенная математическая запись 1 Н Т/Д и 2 Н Т/Д – основное уравнение термодинамики.

1. Изменение энтропии идеального газа при переходе из 1-2: - изменение энтропииv-молекул идеального газа при переходе из 1-2.

1) V=const. 2) T=const.

3) p=const

2. Изменение энтропии при плавлении. При p= const – плавление происходит при T=const.

. Приведенные примеры вычисления энтропии показывают что по изменению энтропии можно судить о направлении протекающих процессов.

Вопрос 37. Реальные газы. Отступление от законов идеальных газов. Взаимодействие молекул. Уравнение Ван-дер-Ваальса. Анализ уравнения Ван-дер-Ваальса.

Как известно, уравнение состояния устанавливает функциональную связь между давлением p, объемом V, температурой T и числом молей n газа в состоянии равновесия. Эта связь может выражаться не только в форме уравнения, но также графически или в виде таблиц, которые часто используются, особенно для практических целей. Самым простым и известным уравнением состояния является уравнение состояния идеального газа: pV = nRT - где R – универсальная газовая постоянная. Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации. Причинами этого являются: 1)собственное размножение молекул; 2)сила взаимодействия между молекулами. В реальных газах молекулы взаимодействуют и эти силы взаимодействия сильно зависят от расстояния между молекулами. На расстоянии больше чем см силы взаимодействия малы. Между молекулами одновременно действует и силы притяжения и силы отталкивания которые меняются в зависимости от расстояния между молекулами. При малых расстояниях преобладают силы отталкивания, при больших расстояниях – силы притяжения. По мере сближения молекул начинают преобладать как силы притяжения, так и силы отталкивания только с разными скоростями.

- некоторое состояние- эффективный диаметр молекулы. при r>r0-силы притяжения и проекции результирующей силы ниже Or. При приближении второй молекулы к первой Δr<0-эта результирующая сила совершает положит работу. Так как работу в З.С. равна изменению потенциальной

энергии со знаком минус, то при r>r0, - системы будет отрицат.

На расстоянии и результирующая этих сил равна 0,при этом 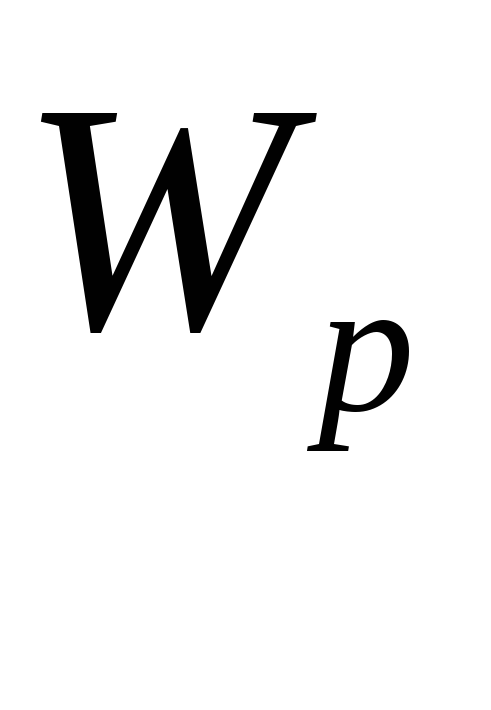- минимальна, а кинетическая максимальна. С уменьшением расстояния будут возрастать быстрее чеми силы отталкивания совершать отрицательную работу. Кинетическая убывает, потенциальная возрастает. Используя модель голландского ученого Ван-дер-Ваальс предложил уравнение состояния для 1 моля реального газа которое носи его имя.

- поправка на силы взаимодействия. b-поправка на собственное размножение молекул.

Это уравнение лучше описывает состояние газа чем уравнение Клайперона.