Уравнение движения абсолютно твёрдого тела

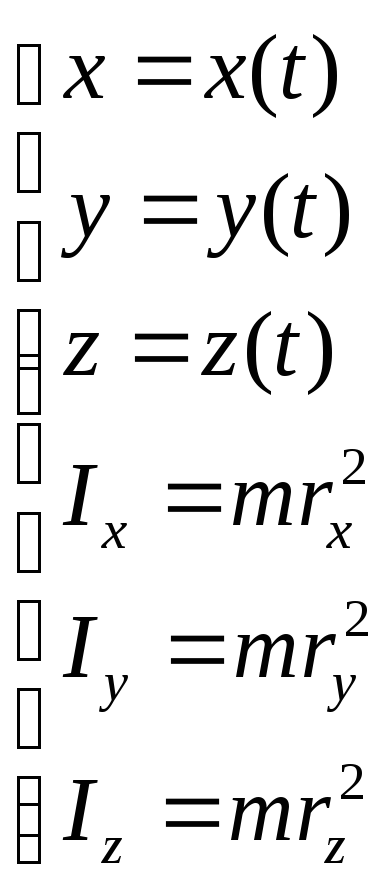
Где первые три уравнения – уравнения поступательного движения (движения центра масс), остальные – уравнения вращательного движения вокруг оси, проходящей через центр масс тела.

25. Вращение твёрдого тела относительно неподвижной оси. Уравнения движения.

Вращением твёрдого телавокруг неподвижной оси называется движение твёрдого тела, при котором все точки прямой, жёстко связанной с телом, остаются неподвижными. Прямая называется осью вращения тела. Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы. Его положение однозначно определяется значением угла поворота вокруг оси вращения из некоторого условно выбранного начального положения этого тела.

Уравнение динамики тела вращающегося вокруг неподвижной оси имеет вид:

dL_z/dt=M_z^внеш., гдеL_z– является моментом импульса вращающегося тела относительно оси вращения, аM_z^внеш– главный момент внешних сил.

26. Момент инерции тела относительно неподвижной оси. Теорема Штейнера.

Величина I, равная сумме произведений массm_iвсех материальных точек, образующих механическую систему, на квадраты их расстояний ρ_iот данной оси, называетсямоментом инерции системы относительно этой оси.

Подсчёт момента инерции тела относительно произвольной оси облегчается ,если воспользоваться теоремой Штейнера: момент инерции I_aтела относительно произвольной оси а равен сумме момента инерцииI_Стела относительно параллельной ей оси а_С, проходящей через центр масс С тела, и произведение массыmна квадрат расстоянияdмежду этими осями.

I_a=I_С+md²(26.1)

Доказательство:

а и а_С– оси,dm– масса малого элемента тела, ρ, ρ_С– расстояние от малого элемента тела до осей а и а_С. По теореме косинусов: ρ²=ρ_С²+d²+2dρ_СcosφиI_a=∫_(m)ρ²dm=∫_(m)ρ_С²dm+md²+2d∫_(m)x^*dm, гдеx^*=ρ_Сcosφ– абсцисса элементаdmтела в системе координат с началом в центре масс тела и осью абсцисс, пересекающей оси а и а_Си лежащий в перпендикулярной им плоскости. Из определения центра масс следует, что ∫_(m)x^*dm=mx^*_C=0, так как центр масс тела совпадает с началом координат. Таким образом, справедливость соотношения (26.1) доказана.

27. Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси.

Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m₁,m₂,…,m_n, находящиеся на расстоянииr₁,r₂,…,r_n, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусовr_iи имеют различные линейные скоростиυ_i.Кинетическую энергию вращающегося теланайдём как сумму кинетических энергий его элементарных объёмов.

T_вр=∑ⁿ_i=1m_iυ_i²/2=∑ⁿ_i=1m_iω²r_i²/2=(ω²∑ⁿ_i=1m_ir_i²)/2=I_zω²/2, гдеI_z– момент инерции тела.

28. Плоское движение.

Плоское движение– это такое движение, при котором все участки траектории точки лежат в одной плоскости; это движение, при котором все перемещения лежат в параллельных плоскостях, а оси всех вращений перпендикулярны этим плоскостям. Любое плоское движение можно представить как результат поступательного движения и «чистого» вращения. В качестве примера плоского движения можно рассмотреть движение кабина колеса обозрения.

В случае плоского движения тела энергия движения складывается из энергии поступательного движения и энергии вращения.

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

,

где m– масса катящегося тела; υ_С– скорость центра масс тела;I_С– момент инерции тела относительно оси, проходящей через его центр масс; ω – угловая скорость тела.

29. Свободные оси. Гироскопы.

Для того чтобы сохранить положение оси вращения твёрдого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на неё внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями), и называются главными осями инерции тела).

Гироскопы– массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Одна из разновидностей гироскопов – гироскоп на кардановом подвесе.

Если момент внешних сил относительно закрепленного центра масс гироскопа равен нулю, то момент импульса гироскопа сохраняет свою величину и направление в пространстве. L=const. Следовательно, сохраняет свое положение в пространстве и ось гироскопа.

Если момент внешних сил, приложенных к вращающемуся гироскопу относительно его центра масс, отличен от нуля, то наблюдается явление гироскопического эффекта. Оно состоит в том, что под действием пары сил, приложенной к оси вращающегося гироскопа, ось гироскопа поворачивается вокруг прямой, находящейся под углом 45° к ней, а не вокруг прямой, перпендикулярной к ней.

Если ось гироскопа закреплена подшипниками, то вследствие гироскопического эффекта возникают так называемые гироскопические силы, действующие на опоры, в которых вращается ось гироскопа.Гироскопические силыимеют смысл только во вращающейся системе отсчёта и являются частным случаем кориолисовой силы инерции.

30. Колебания и характеризующие их величины. Собственные колебания.

Колебанияминазываются движения или процессы, которые характеризуются определённой повторяемостью во времени.

Свободными (собственными) колебанияминазываются колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия; колебания, которые совершаются за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармонические колебания– колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.Уравнение гармонических колебаний колебательной величины s:s=Acos(ω₀t+φ) илиs=Asin(ω₀t+φ), гдеA– амплитуда колебаний,ω₀– круговая (циклическая) частота,φ– начальная фаза колебаний в момент времениt=0, (ω₀t+φ) – фаза колебаний в момент времениt.

Период гармонического колебания– промежуток времениT, в течение которого фаза колебания получает приращение 2π, т.е.ω₀(t+T)+φ=(ω₀t+φ)+2π.T=2π/ω₀.

Период колебаний- наименьший промежуток времени, по истечении которого система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный произвольно выбранный момент.

Частота колебаний– число полных колебаний, совершаемых в единицу времени. ν=1/T.

Амплитуда колебаний– это максимальное значение колеблющейся величины.

Фаза колебаний – это значение колеблющейся величины в произвольный момент времени (ω₀t+φ).

31. Гармонический осциллятор. Собственные колебания гармонического осциллятора.

Гармоническим осцилляторомназывается система, совершающая колебания, описываемые уравнением вида:s”+ω₀²s=0. Колебания гармонического осциллятора являются важным примером периодического движения, и служит точной или приближённой моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.

Свободными (собственными) колебаниями гармонического осциллятора называются колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия; колебания, которые совершаются за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий на колебательную систему.

32. Энергия гармонического осциллятора.

Линейный гармонический осциллятор– материальная точка массойm, совершающая прямолинейные гармонические колебания под действием упругой силы.Уравнения движения осциллятораимеет видmd²x/dt²=-kxилиd²x/dt²+kx/m=0. Гдеk– коэффициент, характеризующий упругие свойства пружины.Потенциальная энергия линейного гармонического осциллятора:W_п=kx²/2.

33. Линейный осциллятор с затуханием. Уравнение движение линейного осциллятора и его решение.

Затуханием колебанийназывается постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.

Затухающие колебания– это колебания, амплитуда которых из-за потерь энергии реальной колебательной системы с течением времени уменьшается.

Для рассмотрения затухающих колебаний обычно используют линейные системы– это идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются.

Дифференциальное уравнение свободно затухающих колебаний линейной системы задаётся в виде:

, (33.1)

где s– колеблющаяся величина, описывающая тот или иной физический процесс, δ=const–коэффициент затухания, ω₀– циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при δ=0 (при отсутствии потерь энергии) называетсясобственной частотой колебательной системы.

Решение уравнения (33.1) рассмотрим в виде s=e^-δtu(33.2), гдеu=u(t).

После нахождения первой и второй производных выражения (33.2) и подстановки их в (33.1) получим . Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:

. Тогда получим уравнение типа:, решением которого является функцияu=A₀cos(ωt+φ). Таким образом, решение уравнения в случае малых затуханийs=A₀e^-δtcos(ωt+φ),

где δ=r/(2m) в случае механических колебаний и δ=R/(2L) в случае электромагнитных колебаний;- частота затухающих колебаний;A₀e^-δt– амплитуда затухающих колебаний.

Промежуток времени τ=1/δ, в течении которого амплитуда затухающих колебаний уменьшится в eраз, называетсявременем релаксации.

Если A(t) иA(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение:

называетсядекрементом затухания, а его логарифм

-логарифмическим декрементом затухания;N_e– число колебаний, совершаемых за время уменьшения амплитуды вeраз. Логарифмический декремент затухания – постоянная для каждой колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротностиQ, которое при малых значениях логарифмического декремента равна

34. Затухающие колебания линейного осциллятора.

Для пружинного маятника массой m, совершающего малые колебания под действием упругой силыF=-kx, сила трения пропорциональна скорости, т.е.F_тр=-rυ=-rx’, гдеr–коэффициент сопротивления. При данных условиях закон движения маятника будет иметь вид:mx”=-kx-rx’. Используя формулу:

и принимая, что коэффициент затухания δ=r/(2m), получим дифференциальное уравнение затухающих колебаний маятника:. Маятник колеблется по закону

x=A₀e^-δtcos(ωt+φ)с частотой:

Добротность пружинного маятника .

35. Логарифмический декремент затухания и добротность осциллятора.

Промежуток времени τ=1/δ, в течении которого амплитуда затухающих колебаний уменьшится в eраз, называетсявременем релаксации.

Если A(t) иA(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение:

называетсядекрементом затухания, а его логарифм

-логарифмическим декрементом затухания;N_e– число колебаний, совершаемых за время уменьшения амплитуды вeраз. Логарифмический декремент затухания – постоянная для каждой колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротностиQ, которое при малых значениях логарифмического декремента равна

37. Вынужденные колебания линейного осциллятора при периодическом воздействии.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющегося по гармоническому закону:X(t)=X₀cosωt.

Переменная внешняя сила, приложенная к системе и вызывающая её вынужденные механические колебания называется вынуждающей, или возмущающей силой.

Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая силаF=F₀cosωt.

Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону Э.Д.С. или переменное напряжениеU=U_mcosωt.

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся Э.Д.С., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

38. Амплитуда и фаза установившихся вынужденных колебаний. Резонанс.

Амплитуда вынужденных колебаний -

Сдвиг фаз между колебаниями и вынуждающей силой:

.

Рассмотрим зависимость амплитуды вынужденных колебаний от частоты.

Чтобы определить резонансную частотуω_рез– частоту, при которой амплитуда смещений (заряда) достигает максимума, - нужно найти максимум функции

. Продифференцировав подкоренное выражение по ω и прировняв к нулю, получим условие, определяющее ω_рез:

. Следовательно резонансная частота.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к резонансной частоте называется резонансом(соответственно механическим или электрическим).

Подставляя формулу в формулу, получим. (Выражение для резонансной амплитуды)

42. Волновое движение. Виды волн.

Колебания, возбуждённые в какой-либо точке среды, распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой.

Чем дальше расположены частицы среды от источника колебаний, тем позднее она начнёт колебаться.

При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т.е. непрерывно распределённая в пространстве и обладающая упругими свойствами.

Волновой процесс(или волна) – это процесс распространения колебаний в сплошной среде, т.е. непрерывно распределённой в пространстве и обладающей упругими свойствами. Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразных волн встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны.

Упругие (или механические волны)– это механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространении волны, а в поперечных – в плоскостях, перпендикулярных направлению распространению волны. Упругая волна называетсягармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Электромагнитные волны– это переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью.

43. Уравнение плоской бегущей волны. Волновые уравнения.

Бегущими волнаминазываются волны, которые переносят в пространстве энергию. Рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а осьxсовпадает с направлением распростронения волны. В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково то смещение ξ будет зависеть только от х иt, т.е. ξ=ξ(x,t). Если колебания точек, лежащих в плоскости х=0, описываются функцией ξ(0,t)=Acosωt, то частицы среды колеблются по тому же закону, но её колебания будут отставать по времени от колебаний источника на τ, так как для прохождения волной расстояния х требуется время τ=х/υ, где υ – скорость распростронения волны. Тогда уравнение колебания частиц примет вид: ξ(x,t)=Acosω(t-x/υ) (43.1).

Уравнение (43.1) есть уравнение бегущей волны. В общем случае уравнение плоской волны, не поглощающей энергию имеет вид ξ(x,t)=Acos[ω(t-x/υ)+φ₀]

Уравнение сферической волны– волны, волновые поверхности которой имеют вид концентрических сфер, имеет вид ξ(r,t)=[A₀cos(ωt-kr+ φ₀)]/r, гдеr– расстояние от центра волны до рассматриваемой точки среды иk– волновое числоk=2π/λ=2π/υT=ω/υ.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных

∂²ξ/∂x²+∂²ξ/∂y²+∂²ξ/∂z²=∂²ξ /υ²∂t². или Δξ=∂²ξ /υ²∂t², где υ – фазовая скорость, Δ=∂²/∂x²+∂²/∂y²+∂²/∂z²– оператор Лапласа.

44. Синусоидальные волны. Фазовая скорость. Длина волны.

Синусоидальная волна– бесконечная, не затухающая упругая волна.

Если волна синусоидальнаято ∂²s/∂t²=-ω²sи Δ²s+k²s=0. Скорость распростронения синусоидальной волны называется фазовой скоростью. Она равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы синусоидальной волны. В случае плоской синусоидальной волныdx/dt=ω/k=υ. В случае сферической синусоидальной волныdr/dt=ω/k=υ. В случае продольной волны в однородной газообразной среде υ=(K/ρ)^1/2, где ρ – плотность газа,K– коэффициент упругости среды. В случае поперечных упругих волн не ограниченной изотропной твёрдой среде υ=(G/ρ)^1/2, гдеG– модуль сдвига среды, ρ - её плотность. В случае продольных волн в тонком стержне υ=(E/ρ)^1/2, гдеE– модуль Юнга для материала стержня, ρ - его плотность. В случае поперечных волн в струне υ=(F/ρS)^1/2, гдеF– сила натяжения струны, ρ иS– плотность материала струны и площадь её поперечного сечения.

Длина волны (λ)– расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Длина волны равна тому расстоянию, на которое распространяется определённая фаза колебания за период.

45. Принцип суперпозиции волн. Групповая скорость.

Принцип суперпозиции (наложения) волн– при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. За скорость распростронения не гармонической волны принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии чтоtdω-xdk=const, получимdx/dt=dω/dk=U. СкоростьUи естьгрупповая скорость. Её можно определить как скорость движения группы волн, образующих в каждый момент времени, локализованный в пространстве волновой пакет. В теории относительности доказывается, что групповая скоростьU≤с, в то время как для фазовой скорости ограничения не существует.

53. Уравнение состояния идеального газа.

Идеальным называется газ, молекулы которого имеют пренебрежимо малый объём и не взаимодействуют друг с другом на расстоянии; это идеализированная модель, согласно которой:

1. Собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;

2. Между молекулами газа отсутствуют силы взаимодействия;

3. Столкновение молекул газа между собой и со стенками сосуда абсолютно упругие.

Русский учёный Д.И. Менделеев объединил уравнение Клайперона с законом Авагадро, отнеся уравнение Клайперона к одному молю, использовав молярный объём V_m. Согласно закону Авагадро, при одинаковых давлении и температуре моли всех газов занимают одинаковый молярный объём, поэтому постоянная В будет одинакова для всех газов. Эта общая для всех газов постоянная обозначаетсяRи называетсямолярной газовой постоянной. Уравнению

PV_m=RT– удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым такжеуравнением Клайперона-Менделеева.

54. Функции состояния. Внутренняя энергия.

1.Закон Бойля-Мариотта: произведение объёма данной массы газа на его давление есть величина постоянная при неизменной температуре.

2.Закон Гей-Люссака: коэффициенты объёмного расширения всех газов одинаковы и равны (отношение объёма данной массы газа к его температуре есть величина постоянная при неизменном давлении).

3.Закон Шарля: температурные коэффициенты давления всех газов одинаковы и равны (отношение давления данной массы газа к его температуре есть величина при неизменном объёме).

Важной характеристикой термодинамической системы является её внутренняя энергияU– энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер, ионов и т.д.) и энергия взаимодействия этих частиц; энергия всевозможных видов движения и взаимодействия всех частиц, образующих систему.

Внутренняя энергия– это однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определённой внутренней энергией (она не зависит от того, как система пришла в данное состояние).

55. Распределение Больцмана.

В классической статистической физики выводятся закон Больцманао равномерном распределении энергии по степеням свободы молекул – для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходятся в среднем кинетической энергии, равнаяkT/2, а на каждую колебательную степень свободы – в среднем энергия, равнаяkT.

Колебательная степень обладает вдвое большей энергией, так как на неё приходятся не только кинетическая энергия (как в случае поступательного и вращательного движения), но и потенциальная, причем среднее значения кинетической и потенциальной энергий одинаково. Таким образом средняя энергия молекулы <ε>=ikT/2, гдеi– сумма числа вращательных, числа поступательных и удвоенного числа колебательных степеней свободы молекулы:i=i_пост+i_вращ+2i_колеб. Так как в идеальном газе взаимная потенциальная энергия равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесённая к одному молю газа, будет равна сумме кинетических энергийN_Aмолекул:U_m=ikTN_A/2=iRT/2. Внутренняя энергия для произвольной массы газаU=miRT/2M=νiRT/2, где М – молярная масса, ν – количество вещества.

56. Распределение Максвелла.

Закон распределения по скоростям теплового движения молекул газа, находящегося в состоянии термодинамического равновесия, впервые был найден Д.К. Максвеллом, называется распределением Максвелла. Скорости молекул удобно изображать в виде полярных векторов в трёхмерном пространстве скоростей. Пустьdn– число молекул в единице объёма газа, модули скоростей которых заключены в пределах отUдоU+dU. Концы векторов этих молекул должны лежать в пространстве скоростей внутри шарового слоя. Объём этого слояdω=4πU²dU. При тепловом движении из-за его беспорядочности все направления скоростей молекул равновероятны. Поэтому числоdnдолжно быть пропорционально как числуn₀молекул в еденице объёма газа, так и объёмуdωшарового слоя. Кроме того,dnдолжно зависить от модуля скоростиU. Таким образомdn=n₀f(U)×4πU²dU=n₀F(U)dU, гдеF(U)=4πU²f(U). Функция распределенияF(U)=dn/n₀dUпредставляет собой долю молекул, модули скоростей которых находятся в шаровом слое единичной толщины. ФункцияF(U) называется функцией распределения молекул газа по модулям их скоростей.

Закон распределения молекул по скоростям (закон Максвелла): dn=(m₀/2πkT)^3/2×e^-(m₀^U×U)/2kT.

U_в – наиболее вероятная скорость молекул газа.

График

57. Явления переноса. Диффузия.

Если в газе существует пространственная неоднородность плотности, температуры при скорости упорядоченного перемещения отдельных слоев газа, то происходит самопроизвольное выравнивание этих неоднородностей. В газе возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки, характерные для неравновесных состояний газа ,являются физической основой особых процессов, объединенных под названием явления переноса.

Диффузиейв простейшем случае называется явлением самопроизвольного взаимного проникновения и перемешивания частиц двух соприкасающихся газов (диффузия может происходить также в жидкостях и твёрдых телах). В химически чистых газах при постоянной температуре диффузия возникает вследствие неодинаковой плотности в различных частях объёма газа. Для смеси газов диффузия вызывается различием в концентрациях отдельных газов в разных частях объёма смеси. При постоянной температуре явление диффузии заключается в переносе массы газа из мест с большей концентрацией данного газа в места с меньшей его концентрацией.

Явление диффузиидля химически однородного газа подчиняетсязакону Фика:

, гдеj_m– плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную осиOx,D– диффузия (коэффициент диффузии),dρ/dx– градиент плотности.

Коэффициент диффузии численно равен плотности потока массы при градиенте плотности, равном единице. D=1/3<υ><l>, где <υ> - средняя скорость теплового движения молекул, <l> - средняя длина свободного пробега.

58. Явление переноса. Теплопроводность.

Если в газе существует пространственная неоднородность плотности, температуры при скорости упорядоченного перемещения отдельных слоев газа, то происходит самопроизвольное выравнивание этих неоднородностей. В газе возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки, характерные для неравновесных состояний газа ,являются физической основой особых процессов, объединенных под названием явления переноса.

Теплопроводностьвозникает при наличии разности температур, вызванной какими-либо внешними причинами. При этом молекулы газа в разных местах его объёма имеют разные средние кинетические энергии и хаотическое тепловое движение молекул приводят к направленному переносу внутренней энергии газа. Молекула, попавшая из нагретых частей объёма газа в более холодные, отдают часть своей энергии окружающим частицам. Наоборот, медленнее движущиеся молекулы, попадая из холодных частей объёма газа в более нагретые, увеличивают свою энергию за счёт соударений с молекулами, имеющими большие скорости и энергии.

Перенос энергии в форме теплоты подчиняется закону Фурье:

, гдеj_E– плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку перпендикулярную осиOx, λ – теплопроводность,dT/dx– градиент температуры.

λ=1/3С_Vρ<υ><l>, гдеC_V– удельная теплоёмкость газа при постоянном объёме, ρ – плотность газа, <υ> - средняя скорость теплового движения молекул, <l> - средняя длина свободного пробега.

59. Явление переноса. Вязкость.

Если в газе существует пространственная неоднородность плотности, температуры при скорости упорядоченного перемещения отдельных слоев газа, то происходит самопроизвольное выравнивание этих неоднородностей. В газе возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки, характерные для неравновесных состояний газа, являются физической основой особых процессов, объединенных под названием явления переноса.

Внутренне трение (вязкость) связанно с возникновением сил трения между слоями газов, перемещающимися параллельно друг другу с различными по модулю скоростями (в жидкости вязкость возникает таким же образом). Со стороны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающиеся слои тормозят более быстро движущиеся слои газа. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоёв. С молекулярно-кинетической точки зрения причиной вязкости является наложение упорядоченного движения слоёв газа с различными скоростями хаотического теплового движения молекулы.

Сила внутреннего трения между двумя слоями газа (жидкости) подчиняются закону Ньютона:

, гдеη– динамическая вязкость,dυ/dx– градиент скорости,S– площадь, на которую действует силаF.

Выражение закона Ньютона можно представить также в виде: , гдеj_p– плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении осиOxчерез единичную площадку, перпендикулярную осиOx.

η=1/3ρ<υ><l>, где ρ – плотность газа, <υ> - средняя скорость теплового движения молекул, <l> - средняя длина свободного пробега.

63. Теплоёмкость идеального газа.

Теплоёмкость– это физическая величина, численно равная отношению количества теплоты, сообщаемого телу, к изменению температуры тела в термодинамическом процессе.

Классический статистический метод изучения тепловых свойств веществ позволил теоретически вычислить теплоёмкости газов и твёрдых тел.

Классическая теория теплоемкости газов приводит к серьезным расхождениям с опытными данными.

Молярные теплоёмкостиC_VиC_P:C_V=iR/2;C_P=(i+2)R/2.

Уравнение Майера показывает, что C_Pвсегда большеC_Vна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объёма газа.

Удельная теплоёмкость вещества– величина, определяемая количеством теплоты, необходимым для нагревания 1кг вещества на 1К.

Формула, связывающая удельную теплоёмкость с молярной: C_m=cM, гдеM– молярная масса вещества.

64. Энтропия.

Помимо внутренней энергии, в термодинамике широко пользуются и другими функциями состояния термодинамической системы.

Для выяснения физического содержания этого понятия рассматривают приведённое количество теплоты– физическая величина, равная отношению количества теплоты, полученного телом в изотермическом процессе, к температуре теплоотдающего тела.Приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно δQ/T.

Приведённое количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю.

Подынтегральное выражение δQ/T– полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.

Энтропия – это функция состояния, полным дифференциалом которой является δQ/T.

Для обратимых процессов изменение энтропии ΔS=0, для необратимых процессов ΔS>0. Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению её энтропии – принцип возрастания энтропии.

Формула Больцмана S=klnW, гдеk– постоянная

65. Второе и третье начало термодинамики.

Появление второго начала термодинамики – необходимость дать ответ на вопрос, какие процессы в природе возможны, а какие нет – определяет направления развития процессов.

Используя понятия энтропии и неравенства Клазиуса, второе начало термодинамикиможно сформулировать как закон возрастания энтропии в замкнутой системе при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает.