23. Ранг матрицы. Свойства ранга.

Следствия:

• Если ранг матрицы равен , то любыестрок или столбцов этой матрицы будут линейно зависимы.

• Если — квадратная матрица, и, то строки и столбцы этой матрицы линейно зависимы.

• Пусть , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно.

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из другаэлементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны.

Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

24. Линейная зависимость столбцов матрицы. Свойства Линейная зависимость и независимость строк (столбцов) матрицы

В предыдущем разделе были введены операции умножения матриц на число и сложения матриц, в частности, для матриц-столбцов и матриц-строк . Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.

Столбец называется линейной комбинацией столбцов одинаковых размеров, если

где — некоторые числа. В этом случае говорят, что столбец разложен по столбцам , а числа называют коэффициентами разложения. Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Если столбцы в (3.1) имеют вид

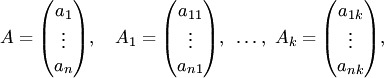то матричному равенству (3.1) соответствуют поэлементные равенства

Аналогично формулируется определение линейной комбинации строк одинаковых размеров.

Набор столбцов одинаковых размеров называется системой столбцов.

Система из столбцов называется линейно зависимой, если существуют такие числа , не все равные нулю одновременно, что

Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.

Система из столбцов называется линейно независимой, если равенство (3.2) возможно только при , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).

Замечания 3.1

1. Один столбец тоже образует систему: при — линейно зависимую, а при линейно независимую.

2. Любая часть системы столбцов называется подсистемой.

Пример 3.1. Используя определение, установить линейную зависимость или линейную независимость систем столбцов

Решение. 1) Столбцы линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами , которая равна нулевому столбцу: .

2) Столбцы линейно независимы, так как равенство

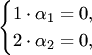 равносильное системе  оказывается верным только при .