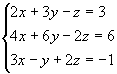- •Свойства
- •[Править]Неравенство Коши — Буняковского
- •Нормальное уравнение плоскости.
- •Общее уравнение прямой - основные сведения.
- •Переход от общего уравнения прямой
- •13,14,15,16 В отдельном файле
- •17. Цилиндрические поверхности с образующей, параллельной одной из координатных осей.
- •18. Матрицы. Линейные операции над матрицами, их свойства.
- •19. Нелинейные операции над матрицами (умножение, транспонирование), их свойства. Умножение матриц
- •Транспонирование и эрмитово сопряжение
- •20. Обратная матрица. Теорема существования, единственность, свойства.
- •21. Матричные уравнения. Теорема существования и единственности решения.
- •22. Решение системы линейных уравнений матричным методом. Правило Крамера.
- •23. Ранг матрицы. Свойства ранга.
- •24. Линейная зависимость столбцов матрицы. Свойства Линейная зависимость и независимость строк (столбцов) матрицы
- •Свойства линейно зависимых и линейно независимых столбцов матриц
- •25. Базисный минор. Теорема о базисном миноре. Теорема о ранге.
- •26. Системы линейных уравнений. Теорема Кронекера - Капелли о совместимости систем.
- •27. Однородные системы линейных уравнений. Свойства их решений. Общее решение ослу.
- •28. Фундаментальная система решений ослу
- •29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
- •30. Линейные пространства. Определение. Примеры, следствия из аксиом.
- •31. Линейная зависимость векторов линейного пространства. Свойства
- •32. Базис линейного пространства. Размерность
- •33. Единственность разложения векторов по базису. Координаты. Действия над векторами в координатной форме.
- •34. Изменение координат вектора при переходе к новому базису. Матрица перехода.
- •35. Евклидово пространство. Определение, примеры. Модуль вектора. Угол между векторами. Неравенство Коши-Буняковского.
- •36. Линейный оператор. Матрица линейного оператора. Изменение матрицы линейного оператора при переходе к новому базису.
- •37. Образ и ядро линейного оператора. Ранг линейного оператора.
- •38.В отдельном файле.
- •39. Собственные векторы и собственные значения линейного оператора. Их свойства
- •40. Последовательность. Предел последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. Определение
- •[Править]Примеры
- •[Править]Операции над последовательностями
- •[Править]Подпоследовательности
- •[Править]Примеры
- •[Править]Свойства
- •[Править]Предельная точка последовательности
- •[Править]Предел последовательности
- •[Править]Некоторые виды последовательностей
- •[Править]Ограниченные и неограниченные последовательности
- •[Править]Критерий ограниченности числовой последовательности
- •[Править]Свойства ограниченных последовательностей
- •[Править]Бесконечно большие и бесконечно малые последовательности
- •[Править]Свойства бесконечно малых последовательностей
- •[Править]Сходящиеся и расходящиеся последовательности
- •[Править]Свойства сходящихся последовательностей
- •41. Понятие функции. Способы задания функции.
- •42. Предел функции в точке, в бесконечности. Геометрическая интерпретация. Определения и примеры.
- •43. Теоремы о пределах:
- •44. Непрерывные функции и их свойства:
- •Свойства Локальные
- •Глобальные
- •Теорема о сохранении знака для непрерывной функции
- •Доказательство
- •45. Первый замечательный предел. Следствия. Теорема о пределе суммы, произведения и частного.
- •46. Ограниченные функции и их свойства. Необходимое условие существования предела функции в точке.
- •47. Бесконечно малые функции, их свойства. Леммы
- •Леммы о бесконечно малых
- •48. Критерий существования предела функции в точке.
- •49. Бесконечно большие функции, связь с бесконечно малыми функциями.
- •50. Раскрытие неопределенностей. Второй замечательный предел.
- •51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
- •52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
- •3.2. Основные формулы эквивалентности бесконечно малых.
- •53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
- •54. Точки разрыва функции и их классификация.
- •55. Свойства функций, непрерывных на отрезке.
- •56. Задачи, приводящие к понятию производной. Понятие производной. Геометрический и физический смысл производной.
- •1.1 Задачи, приводящие к понятию производной
- •, Если .
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •58. Производная сложной функции.
- •59. Дифференциал функции. Инвариантность формы записи первого дифференциала.
- •60. Обратная функция и ее производная.
- •60. Обратная функция и ее производная.
- •61. Правила дифференцирования.
- •63. Логарифмическое дифференцирование. Производная степенно-показательной функции.
- •5.4. Производная степенно-показательной функции
- •64. См. Отдельный файл.
- •65. Теоремы о среднем – Ферма, Ролля.
- •66. Теоремы о среднем – Лагранжа, Коши.
- •67. Дифференциалы высших порядков. Неинвариантность формы записи.
- •68. Правило Лопиталя. Раскрытие неопределенностей с использованием правила Лопиталя.
- •69. Формула Тейлора. Разложение функции по формуле Тейлора.
- •70. Монотонность функции. Условия монотонности.
- •71. Экстремумы функции. Необходимое условие существования экстремума.
- •72. Достаточные условия экстремума.
- •73. Выпуклость и вогнутость графика функции. Точки перегиба.
- •74. Асимптоты графика.
- •[Править]Виды асимптот графиков [править]Вертикальная
- •[Править]Горизонтальная
- •[Править]Наклонная
- •[Править]Нахождение асимптот
- •76. Метод замены переменных в неопределенном интеграле.
- •77. Интегрирование по частям в неопределенном интеграле. Классы функций, интегрируемых по частям.
- •78. Рациональные дроби. Разложение рациональных дробей на сумму простейших.
- •79. Интегрирование простейших рациональных дробей.
- •80. Интегрирование тригонометрических функций.
- •81. Интегрирование иррациональностей вида…
- •82. Интегрирование иррациональностей вида…
- •83. Понятие определенного интеграла, его геометрический смысл и свойства. Теорема о среднем.
- •84. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •85. Полярная система координат. Уравнения кривых в полярной системе координат.
- •Уравнение кривых в полярных координатах
- •Окружность
- •Полярная роза
- •Спираль Архимеда
- •Конические сечения
- •86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
- •87. Вычисление объемов тел, объемов тел вращения.
- •88. Приложение определенного интеграла к задачам физики.
- •89. Несобственные интегралы I рода.
- •89. Несобственные интегралы I рода.
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •90. Несобственные интегралы II рода.
- •Геометрический смысл несобственных интегралов II рода
21. Матричные уравнения. Теорема существования и единственности решения.
Рассмотрим матричное уравнение вида
![]()
|
(4.5) |
где ![]() и
и ![]() —
данные матрицы, имеющие одинаковое
количество строк, причем матрица
—
данные матрицы, имеющие одинаковое
количество строк, причем матрица ![]() квадратная.
Требуется найти матрицу
квадратная.
Требуется найти матрицу ![]() ,
удовлетворяющую уравнению (4.5).
,
удовлетворяющую уравнению (4.5).
Теорема
4.2 о существовании и единственности
решения матричного уравнения (4.5). Если
определитель матрицы ![]() отличен
от нуля, то матричное уравнение (4.5) имеет
единственное решение
отличен
от нуля, то матричное уравнение (4.5) имеет
единственное решение![]() .
.
В
самом деле, подставляя ![]() в
левую часть равенства (4.5), получаем
в
левую часть равенства (4.5), получаем![]() ,
т.е. правую часть этого равенства.
,
т.е. правую часть этого равенства.
Заметим,
что решением матричного уравнения ![]() служит
обратная матрица
служит
обратная матрица![]() .
.
Рассмотрим также матричное уравнение вида
![]()
|
(4.6) |
где ![]() и
и ![]() —
данные матрицы, имеющие одинаковое
количество столбцов, причем
матрица
—
данные матрицы, имеющие одинаковое
количество столбцов, причем
матрица ![]() квадратная.
Требуется найти матрицу
квадратная.
Требуется найти матрицу ![]() ,
удовлетворяющую уравнению (4.6).
,
удовлетворяющую уравнению (4.6).
Теорема
4.3 о существовании и единственности
решения матричного уравнения (4.6). Если
определитель матрицы ![]() отличен
от нуля, то уравнение (4.6) имеет единственное
решение
отличен
от нуля, то уравнение (4.6) имеет единственное
решение![]() .
.
Заметим,
что матрица ![]() является
как бы "левым" частным от "деления"
матрицы
является
как бы "левым" частным от "деления"
матрицы![]() на
матрицу
на
матрицу![]() ,
поскольку матрица
,
поскольку матрица![]() в
(4.5) умножается на
в
(4.5) умножается на![]() слева,
а матрица
слева,
а матрица![]() —
"правым" частным, так как матрица
—
"правым" частным, так как матрица![]() в
(4.6) умножается на
в
(4.6) умножается на![]() справа.
справа.
Пример 4.5. Даны матрицы

Решить
уравнения: а) ![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение. Обратная
матрица ![]() была
найдена в примере 4.2.
была
найдена в примере 4.2.
а)
Решение уравнения ![]() находим,
умножая обе его части слева на
находим,
умножая обе его части слева на![]()
![]()
б)
Уравнение не имеет решений, так как
матрицы ![]() и
и![]() имеют
разное количество столбцов
имеют
разное количество столбцов![]() .
.
в)
Решение уравнения ![]() находим,
умножая обе его части справа на
находим,
умножая обе его части справа на![]()

Пример
4.6. Решить
уравнение: ![]() ,
где
,
где![]() .
.
Решение. Преобразуя левую часть уравнения:
![]()
приведем его к виду (4.1)
![]() где
где
Следовательно, ![]() .
Обратная матрица найдена в примере 4.2:
.
Обратная матрица найдена в примере 4.2:
![]() Значит,
Значит, ![]()
Пример
4.7. Решить
уравнение ![]() ,
где
,
где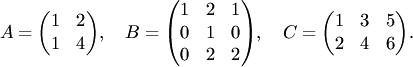
Решение. Обратные
матрицы
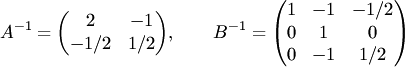 были
найдены в примерах 4.2, 4.3 соответственно.
Решение уравнения находим по формуле
были
найдены в примерах 4.2, 4.3 соответственно.
Решение уравнения находим по формуле

Пример
4.8. Решить
уравнение ![]() ,
где
,
где
![]()
Решение. Определитель
матрицы ![]() равен
нулю, следовательно, обратная матрица
не существует. Поэтому нельзя использовать
формулу
равен
нулю, следовательно, обратная матрица
не существует. Поэтому нельзя использовать
формулу![]() .
Будем искать элементы матрицы
.
Будем искать элементы матрицы![]() .
Подставляя в уравнение, получаем
.
Подставляя в уравнение, получаем
![]()
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:

Здесь,
учитывая пропорциональность уравнений,
в системе оставлены только два уравнения
из четырех. Выразим неизвестные ![]() и
и![]()

Следовательно, решение матричного уравнения имеет вид
![]() где
параметры
где
параметры ![]() и
и ![]() могут
принимать любые значения. Таким образом,
данное матричное уравнение имеет
бесконечное множество решений.
могут
принимать любые значения. Таким образом,
данное матричное уравнение имеет
бесконечное множество решений.
22. Решение системы линейных уравнений матричным методом. Правило Крамера.
|
Рассмотрим систему уравнений |
|
|
|
|
|
|
|
Очевидно,
что |
|
тогда АХ=С Такое равенство называется матричным уравнением.
Если
матрица А системы невырожденная,
(det А Умножим обе его части на матрицу А-1, обратную матрице А А-1(АХ)=А-1С или, (А-1А) · Х = А-1·С. но так как А-1А=Е, и ЕХ=Х Х=А-1С Например, решим матричным способом систему |
|
|
|
|
|
Не является ли матрица А вырожденной? Найдем ее определитель: А =1·[-1·4 – 1·2] – 1·[2·4 – 2·4] + 2·[2·1 – 4·(-1)] = -6 + 12 = 6 Определитель не равен нулю, то есть матрица не вырожденная. Значит, существует обратная матрица А11 = (-1)1+1·М11 = (+1)·[-1·4 – 1·2] = -6 А12 = (-1)1+2·М12 = (-1)·[2·4 – 2·4] = 0 А13 = (-1)1+3·М13 = (+1)·[2·1 – 4·(-1)] = 6 А21 = (-1)2+1·М21 = (-1)·[1·4 – 1·2] = -2 А22 = (-1)2+2·М22 = [1·4 – 2·4] = -4 А23 = (-1)2+3·М23 = (-1)·[1·1 – 4·1] = 3 А31 = (-1)3+1М31 = [1·2 – (-1)·2] = 4 А32 = (-1)3+2·М32 = [(-1)·1·2 – 2·2] = 2 А33 = (-1)3+3·М33 = [1·(-1) – 2·1] = -3 |
|
|
|
|
|
|
Можно убедиться проверкой в правильности решения: подставим вектор Х в первоначальное матричное уравнение.
Действительно вектор Х удовлетворяет заданной системе |
|
Решение систем уравнений методом Крамера Применим теперь наши знания о матрицах к решению систем уравнений первой степени. Рассмотрим систему двух уравнений с двумя неизвестными: |
|
|
или
коротко |
|
система записана в матричном виде (как произведение матриц) Решим эту простенькую систему школьными методами. Умножим первое уравнение на а22, а второе на (-а12) и сложим (а11а22 – а21а12)х1 = с1а22 – с2а12 аналогично (а11а22 – а21а12)х2 = с2а11 – с1а21 |
|
1)
но а11а22 –
а21а12 = |
|
2) определитель, который получится из det А, если в нем столбец коэффициентов при х1 (первый столбец) заменить на столбец правых частей. Обозначим его Х1 |
|
3) |
|
|
Видим,
что |
|
Как вы понимаете, если мы возьмем систему трех уравнений с тремя неизвестными или n уравнений с n неизвестными, то формулы останутся те же:
|
|
Эти формулы широко известны и называются формулами Крамера. Мы же с Вами займемся анализом того существует ли решение и единственно ли оно? Возможны 3 случая:
1.
2. =0 ,
а какой-либо из xi 3. =0 и все xi=0 то система имеет бесконечно много решений. Пример: |
|
|
|
|
|
Так как второе уравнение получается из первого умножением на 2, то наша система равносильна такой системе. |
|
|
|
Так получилось, потому что первое и второе уравнения систем эквивалентны и фактически мы имеем систему двух уравнений с тремя неизвестными, то есть неопределенную систему. Она имеет бесчисленное множество решений. Положив, например, z=0 получим систему |
|
|
|
Решив ее, найдем 11х=0, х=0, y=1 То есть решение первоначальной системы x=0, y=0, z=0. Если бы мы положили z=1, получили бы еще один ответ и так далее. |
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
![]()
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – наA21 и 3-е – на A31:

Сложим эти уравнения:
![]()
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
![]() .
.
Далее рассмотрим коэффициенты при x2:

Аналогично
можно показать, что и ![]() .
.
Наконец
несложно заметить, что 
Таким
образом, получаем равенство: ![]() .
.
Следовательно, ![]() .
.
Аналогично
выводятся равенства ![]() и
и ![]() ,
откуда и следует утверждение теоремы.
,
откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.


 - матрица
системы
- матрица
системы -
матрицы-столбцы неизвестных и свободных
членов.
-
матрицы-столбцы неизвестных и свободных
членов. ,
,
 матрица
системы
матрица
системы
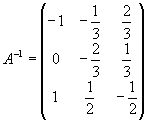



 или
АХ=С
или
АХ=С -
это определитель матрицы А(det А)
или его еще называют определитель
системы и он составлен из коэффициентов
при неизвестных. Обозначим его
-
это определитель матрицы А(det А)
или его еще называют определитель
системы и он составлен из коэффициентов
при неизвестных. Обозначим его