84. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Интеграл с переменным верхним пределом. Значение определённого интеграла не зависит от того, какой буквой обозначена переменная интегрирования: 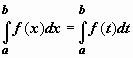(чтобы убедиться в этом, достаточно выписать интегральные суммы, они совпадают). В этом разделе переменную интегрирования будем обозначать буквойt, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела: . Легко доказать, что еслиf(t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема:  Теорема об интеграле с переменным верхним пределом. Если функция f(t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и .Другими словами, производная определённого интеграла от непрерывной функции по верхнему пределу равна значению подынтегральной функции в этом пределе. Док-во. Дадим верхнему пределу x приращение . Тогда, гдеc - точка, лежащая между x и (существование такой точки утверждается теоремой о среднем; цифры над знаком равенства - номер применённого свойства определённого интеграла).. Устремим. При этом(c- точка, расположенная между x и ). Так какf(t) непрерывна в точке t = x, то . Следовательно, существует, и. Теорема доказана.

Отметим первое важное следствие этой теоремы. По существу, мы доказали, что любая непрерывная функция f(x) имеет первообразную, и эта первообразная определяется формулой . Другим важным следствием этой теоремы является формула Ньютона-Лейбница, или основная формула интегрального исчисления.

11.3.2. Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то.Док-во. Мы установили, что функция - первообразная непрерывнойf(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x = a. Так как , то. В равенствепереобозначим переменные: для переменной интегрированияt вернёмся к обозначению x , верхний предел x обозначим b. Окончательно, .Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом:(здесьчитается как "подстановка отa до b"), поэтому формулу Ньютона-Лейбница обычно записывают так: .Пример применения формулы Ньютона-Лейбница:.

85. Полярная система координат. Уравнения кривых в полярной системе координат.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.^[1]

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.