
- •Свойства
- •[Править]Неравенство Коши — Буняковского
- •Нормальное уравнение плоскости.
- •Общее уравнение прямой - основные сведения.
- •Переход от общего уравнения прямой
- •13,14,15,16 В отдельном файле
- •17. Цилиндрические поверхности с образующей, параллельной одной из координатных осей.
- •18. Матрицы. Линейные операции над матрицами, их свойства.
- •19. Нелинейные операции над матрицами (умножение, транспонирование), их свойства. Умножение матриц
- •Транспонирование и эрмитово сопряжение
- •20. Обратная матрица. Теорема существования, единственность, свойства.
- •21. Матричные уравнения. Теорема существования и единственности решения.
- •22. Решение системы линейных уравнений матричным методом. Правило Крамера.
- •23. Ранг матрицы. Свойства ранга.
- •24. Линейная зависимость столбцов матрицы. Свойства Линейная зависимость и независимость строк (столбцов) матрицы
- •Свойства линейно зависимых и линейно независимых столбцов матриц
- •25. Базисный минор. Теорема о базисном миноре. Теорема о ранге.
- •26. Системы линейных уравнений. Теорема Кронекера - Капелли о совместимости систем.
- •27. Однородные системы линейных уравнений. Свойства их решений. Общее решение ослу.
- •28. Фундаментальная система решений ослу
- •29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
- •30. Линейные пространства. Определение. Примеры, следствия из аксиом.
- •31. Линейная зависимость векторов линейного пространства. Свойства
- •32. Базис линейного пространства. Размерность
- •33. Единственность разложения векторов по базису. Координаты. Действия над векторами в координатной форме.
- •34. Изменение координат вектора при переходе к новому базису. Матрица перехода.
- •35. Евклидово пространство. Определение, примеры. Модуль вектора. Угол между векторами. Неравенство Коши-Буняковского.
- •36. Линейный оператор. Матрица линейного оператора. Изменение матрицы линейного оператора при переходе к новому базису.
- •37. Образ и ядро линейного оператора. Ранг линейного оператора.
- •38.В отдельном файле.
- •39. Собственные векторы и собственные значения линейного оператора. Их свойства
- •40. Последовательность. Предел последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. Определение
- •[Править]Примеры
- •[Править]Операции над последовательностями
- •[Править]Подпоследовательности
- •[Править]Примеры
- •[Править]Свойства
- •[Править]Предельная точка последовательности
- •[Править]Предел последовательности
- •[Править]Некоторые виды последовательностей
- •[Править]Ограниченные и неограниченные последовательности
- •[Править]Критерий ограниченности числовой последовательности
- •[Править]Свойства ограниченных последовательностей
- •[Править]Бесконечно большие и бесконечно малые последовательности
- •[Править]Свойства бесконечно малых последовательностей
- •[Править]Сходящиеся и расходящиеся последовательности
- •[Править]Свойства сходящихся последовательностей
- •41. Понятие функции. Способы задания функции.
- •42. Предел функции в точке, в бесконечности. Геометрическая интерпретация. Определения и примеры.
- •43. Теоремы о пределах:
- •44. Непрерывные функции и их свойства:
- •Свойства Локальные
- •Глобальные
- •Теорема о сохранении знака для непрерывной функции
- •Доказательство
- •45. Первый замечательный предел. Следствия. Теорема о пределе суммы, произведения и частного.
- •46. Ограниченные функции и их свойства. Необходимое условие существования предела функции в точке.
- •47. Бесконечно малые функции, их свойства. Леммы
- •Леммы о бесконечно малых
- •48. Критерий существования предела функции в точке.
- •49. Бесконечно большие функции, связь с бесконечно малыми функциями.
- •50. Раскрытие неопределенностей. Второй замечательный предел.
- •51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
- •52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
- •3.2. Основные формулы эквивалентности бесконечно малых.
- •53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
- •54. Точки разрыва функции и их классификация.
- •55. Свойства функций, непрерывных на отрезке.
- •56. Задачи, приводящие к понятию производной. Понятие производной. Геометрический и физический смысл производной.
- •1.1 Задачи, приводящие к понятию производной
- •, Если .
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •58. Производная сложной функции.
- •59. Дифференциал функции. Инвариантность формы записи первого дифференциала.
- •60. Обратная функция и ее производная.
- •60. Обратная функция и ее производная.
- •61. Правила дифференцирования.
- •63. Логарифмическое дифференцирование. Производная степенно-показательной функции.
- •5.4. Производная степенно-показательной функции
- •64. См. Отдельный файл.
- •65. Теоремы о среднем – Ферма, Ролля.
- •66. Теоремы о среднем – Лагранжа, Коши.
- •67. Дифференциалы высших порядков. Неинвариантность формы записи.
- •68. Правило Лопиталя. Раскрытие неопределенностей с использованием правила Лопиталя.
- •69. Формула Тейлора. Разложение функции по формуле Тейлора.
- •70. Монотонность функции. Условия монотонности.
- •71. Экстремумы функции. Необходимое условие существования экстремума.
- •72. Достаточные условия экстремума.
- •73. Выпуклость и вогнутость графика функции. Точки перегиба.
- •74. Асимптоты графика.
- •[Править]Виды асимптот графиков [править]Вертикальная
- •[Править]Горизонтальная
- •[Править]Наклонная
- •[Править]Нахождение асимптот
- •76. Метод замены переменных в неопределенном интеграле.
- •77. Интегрирование по частям в неопределенном интеграле. Классы функций, интегрируемых по частям.
- •78. Рациональные дроби. Разложение рациональных дробей на сумму простейших.
- •79. Интегрирование простейших рациональных дробей.
- •80. Интегрирование тригонометрических функций.
- •81. Интегрирование иррациональностей вида…
- •82. Интегрирование иррациональностей вида…
- •83. Понятие определенного интеграла, его геометрический смысл и свойства. Теорема о среднем.
- •84. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •85. Полярная система координат. Уравнения кривых в полярной системе координат.
- •Уравнение кривых в полярных координатах
- •Окружность
- •Полярная роза
- •Спираль Архимеда
- •Конические сечения
- •86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
- •87. Вычисление объемов тел, объемов тел вращения.
- •88. Приложение определенного интеграла к задачам физики.
- •89. Несобственные интегралы I рода.
- •89. Несобственные интегралы I рода.
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •90. Несобственные интегралы II рода.
- •Геометрический смысл несобственных интегралов II рода
70. Монотонность функции. Условия монотонности.
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Определения
Пусть
дана функция ![]() Тогда
Тогда
функция
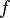 называетсявозраста́ющей на
называетсявозраста́ющей на 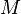 ,
если
,
если
![]() .
.
функция
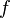 называетсястро́го
возраста́ющей на
называетсястро́го
возраста́ющей на  ,
если
,
если
![]() .
.
функция
 называетсяубыва́ющей на
называетсяубыва́ющей на  ,
если
,
если
![]() .
.
функция
 называетсястро́го
убыва́ющей на
называетсястро́го
убыва́ющей на  ,
если
,
если
![]() .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Другая терминология
Иногда возрастающие функции называют неубыва́ющими, а убывающие функции невозраста́ющими. Строго возрастающие функции тогда зовут просто возрастающими, а строго убывающие просто убывающими.
Свойства монотонных функций
Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция,
 определённая
назамкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.
определённая
назамкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция
 дифференцируема почти
всюду относительно меры
Лебега.
дифференцируема почти
всюду относительно меры
Лебега.
Условия монотонности функции
(Критерий монотонности функции, имеющей производную на интервале) Пусть функция
 непрерывна
на
непрерывна
на и
имеет в каждой точке
и
имеет в каждой точке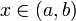 производную
производную  Тогда
Тогда
![]() не
убывает на
не
убывает на ![]() тогда
и только тогда, когда
тогда
и только тогда, когда![]()
![]() не
возрастает на
не
возрастает на ![]() тогда
и только тогда, когда
тогда
и только тогда, когда![]()
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция
 непрерывна
на
непрерывна
на и
имеет в каждой точке
и
имеет в каждой точке производную
производную Тогда
Тогда
если ![]() то
то![]() строго
возрастает на
строго
возрастает на![]()
если ![]() то
то![]() строго
убывает на
строго
убывает на![]()
Обратное,
вообще говоря, неверно. Производная
строго монотонной функции может
обращаться в ноль.
Однако, множество точек, где производная
не равна нулю, должно быть плотнона
интервале ![]() Точнее
имеет место
Точнее
имеет место
(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть
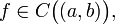 и
всюду на интервале определена
производная
и
всюду на интервале определена
производная Тогда
Тогда строго
возрастает на интервале
строго
возрастает на интервале тогда
и только тогда, когда выполнены следующие
два условия:
тогда
и только тогда, когда выполнены следующие
два условия:
Аналогично, ![]() строго
убывает на интервале
строго
убывает на интервале![]() тогда
и только тогда, когда выполнены следующие
два условия:
тогда
и только тогда, когда выполнены следующие
два условия:
71. Экстремумы функции. Необходимое условие существования экстремума.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. Вматематическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть
дана функция ![]() и
и![]() —
внутренняя точка области определения
—
внутренняя точка области определения![]() Тогда
Тогда
 называется
точкой локального максимума функции
называется
точкой локального максимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность такая,
что
такая,
что
![]()
 называется
точкой локального минимума функции
называется
точкой локального минимума функции 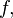 если
существует проколотая окрестность
если
существует проколотая окрестность такая,
что
такая,
что
![]()
Если
неравенства выше строгие, то ![]() называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.
 называется
точкой абсолютного (глобального)
максимума, если
называется
точкой абсолютного (глобального)
максимума, если
![]()
 называется
точкой абсолютного минимума, если
называется
точкой абсолютного минимума, если
![]()
Значение
функции ![]() называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Замечание
Функция ![]() определённая
на множестве
определённая
на множестве![]() может
не иметь на нём ни одного локального
или абсолютного экстремума. Например,
может
не иметь на нём ни одного локального
или абсолютного экстремума. Например,![]()
Необходимые условия существования локальных экстремумов
Из леммы Ферма вытекает следующее:
Пусть
точка ![]() является
точкой экстремума функции
является
точкой экстремума функции![]() ,
определенной в некоторой окрестности
точки
,
определенной в некоторой окрестности
точки![]() .
.
Тогда
либо производная ![]() не
существует, либо
не
существует, либо![]() .
.
(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)
