
- •Свойства
- •[Править]Неравенство Коши — Буняковского
- •Нормальное уравнение плоскости.
- •Общее уравнение прямой - основные сведения.
- •Переход от общего уравнения прямой
- •13,14,15,16 В отдельном файле
- •17. Цилиндрические поверхности с образующей, параллельной одной из координатных осей.
- •18. Матрицы. Линейные операции над матрицами, их свойства.
- •19. Нелинейные операции над матрицами (умножение, транспонирование), их свойства. Умножение матриц
- •Транспонирование и эрмитово сопряжение
- •20. Обратная матрица. Теорема существования, единственность, свойства.
- •21. Матричные уравнения. Теорема существования и единственности решения.
- •22. Решение системы линейных уравнений матричным методом. Правило Крамера.
- •23. Ранг матрицы. Свойства ранга.
- •24. Линейная зависимость столбцов матрицы. Свойства Линейная зависимость и независимость строк (столбцов) матрицы
- •Свойства линейно зависимых и линейно независимых столбцов матриц
- •25. Базисный минор. Теорема о базисном миноре. Теорема о ранге.
- •26. Системы линейных уравнений. Теорема Кронекера - Капелли о совместимости систем.
- •27. Однородные системы линейных уравнений. Свойства их решений. Общее решение ослу.
- •28. Фундаментальная система решений ослу
- •29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
- •30. Линейные пространства. Определение. Примеры, следствия из аксиом.
- •31. Линейная зависимость векторов линейного пространства. Свойства
- •32. Базис линейного пространства. Размерность
- •33. Единственность разложения векторов по базису. Координаты. Действия над векторами в координатной форме.
- •34. Изменение координат вектора при переходе к новому базису. Матрица перехода.
- •35. Евклидово пространство. Определение, примеры. Модуль вектора. Угол между векторами. Неравенство Коши-Буняковского.
- •36. Линейный оператор. Матрица линейного оператора. Изменение матрицы линейного оператора при переходе к новому базису.
- •37. Образ и ядро линейного оператора. Ранг линейного оператора.
- •38.В отдельном файле.
- •39. Собственные векторы и собственные значения линейного оператора. Их свойства
- •40. Последовательность. Предел последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. Определение
- •[Править]Примеры
- •[Править]Операции над последовательностями
- •[Править]Подпоследовательности
- •[Править]Примеры
- •[Править]Свойства
- •[Править]Предельная точка последовательности
- •[Править]Предел последовательности
- •[Править]Некоторые виды последовательностей
- •[Править]Ограниченные и неограниченные последовательности
- •[Править]Критерий ограниченности числовой последовательности
- •[Править]Свойства ограниченных последовательностей
- •[Править]Бесконечно большие и бесконечно малые последовательности
- •[Править]Свойства бесконечно малых последовательностей
- •[Править]Сходящиеся и расходящиеся последовательности
- •[Править]Свойства сходящихся последовательностей
- •41. Понятие функции. Способы задания функции.
- •42. Предел функции в точке, в бесконечности. Геометрическая интерпретация. Определения и примеры.
- •43. Теоремы о пределах:
- •44. Непрерывные функции и их свойства:
- •Свойства Локальные
- •Глобальные
- •Теорема о сохранении знака для непрерывной функции
- •Доказательство
- •45. Первый замечательный предел. Следствия. Теорема о пределе суммы, произведения и частного.
- •46. Ограниченные функции и их свойства. Необходимое условие существования предела функции в точке.
- •47. Бесконечно малые функции, их свойства. Леммы
- •Леммы о бесконечно малых
- •48. Критерий существования предела функции в точке.
- •49. Бесконечно большие функции, связь с бесконечно малыми функциями.
- •50. Раскрытие неопределенностей. Второй замечательный предел.
- •51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
- •52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
- •3.2. Основные формулы эквивалентности бесконечно малых.
- •53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
- •54. Точки разрыва функции и их классификация.
- •55. Свойства функций, непрерывных на отрезке.
- •56. Задачи, приводящие к понятию производной. Понятие производной. Геометрический и физический смысл производной.
- •1.1 Задачи, приводящие к понятию производной
- •, Если .
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •58. Производная сложной функции.
- •59. Дифференциал функции. Инвариантность формы записи первого дифференциала.
- •60. Обратная функция и ее производная.
- •60. Обратная функция и ее производная.
- •61. Правила дифференцирования.
- •63. Логарифмическое дифференцирование. Производная степенно-показательной функции.
- •5.4. Производная степенно-показательной функции
- •64. См. Отдельный файл.
- •65. Теоремы о среднем – Ферма, Ролля.
- •66. Теоремы о среднем – Лагранжа, Коши.
- •67. Дифференциалы высших порядков. Неинвариантность формы записи.
- •68. Правило Лопиталя. Раскрытие неопределенностей с использованием правила Лопиталя.
- •69. Формула Тейлора. Разложение функции по формуле Тейлора.
- •70. Монотонность функции. Условия монотонности.
- •71. Экстремумы функции. Необходимое условие существования экстремума.
- •72. Достаточные условия экстремума.
- •73. Выпуклость и вогнутость графика функции. Точки перегиба.
- •74. Асимптоты графика.
- •[Править]Виды асимптот графиков [править]Вертикальная
- •[Править]Горизонтальная
- •[Править]Наклонная
- •[Править]Нахождение асимптот
- •76. Метод замены переменных в неопределенном интеграле.
- •77. Интегрирование по частям в неопределенном интеграле. Классы функций, интегрируемых по частям.
- •78. Рациональные дроби. Разложение рациональных дробей на сумму простейших.
- •79. Интегрирование простейших рациональных дробей.
- •80. Интегрирование тригонометрических функций.
- •81. Интегрирование иррациональностей вида…
- •82. Интегрирование иррациональностей вида…
- •83. Понятие определенного интеграла, его геометрический смысл и свойства. Теорема о среднем.
- •84. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •85. Полярная система координат. Уравнения кривых в полярной системе координат.
- •Уравнение кривых в полярных координатах
- •Окружность
- •Полярная роза
- •Спираль Архимеда
- •Конические сечения
- •86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
- •87. Вычисление объемов тел, объемов тел вращения.
- •88. Приложение определенного интеграла к задачам физики.
- •89. Несобственные интегралы I рода.
- •89. Несобственные интегралы I рода.
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •90. Несобственные интегралы II рода.
- •Геометрический смысл несобственных интегралов II рода
, Если .
Если
же![]() ,
то касательная к кривой y = f(x) в точке
,
то касательная к кривой y = f(x) в точке![]() будет
иметь вид
будет
иметь вид ![]() ,
а нормаль
,
а нормаль![]()
57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
Функция ![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке ![]() ,
предельной для множестваE,
если ее приращение Δf(x0),
соответствующее приращению аргумента x,
может быть представлено в виде
,
предельной для множестваE,
если ее приращение Δf(x0),
соответствующее приращению аргумента x,
может быть представлено в виде
Δf(x0) = A(x0)(x - x0) + ω(x - x0), (1)
где ω(x - x0) = о(x - x0) при x → x0.
Отображение ![]()
![]() ,
называетсядифференциалом функции f в
точке x0,
а величина A(x0)h - значением
дифференциала в
этой точке.
,
называетсядифференциалом функции f в
точке x0,
а величина A(x0)h - значением
дифференциала в
этой точке.
Для значения дифференциала функции f принято обозначение df или df(x0), если требуется знать, в какой именно точке он вычислен. Таким образом,
df(x0) = A(x0)h.
Разделив
в (1) на x - x0 и
устремив x к x0,
получим A(x0)
= f'(x0).
Поэтому ![]() имеем
имеем
df(x0) = f'(x0)h. (2)
Сопоставив (1) и (2), видим, что значение дифференциала df(x0) (при f'(x0) ≠ 0) есть главная часть приращения функции f в точке x0, линейная и однородная в то же время относительно приращения h = x - x0.
Критерий дифференцируемости функции
Для того чтобы функция f являлась дифференцируемой в данной точке x0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
58. Производная сложной функции.
Функции
сложного вида не совсем корректно
называть термином «сложная функция».
К примеру,  смотрится
очень внушительно, но сложной эта функция
не является, в отличие от
смотрится
очень внушительно, но сложной эта функция
не является, в отличие от![]() .
.
В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.
При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.
Сложная функция – это функция, аргументом которой также является функция.
С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).
К
примеру, пусть f –
функция арктангенса, а g(x)
= lnx есть
функция натурального логарифма, тогда
сложная функция f(g(x)) представляет
собой arctg(lnx).
Еще пример: f –
функция возведения в четвертую степень,
а ![]() -
целая рациональная функция
(смотритеклассификацию
элементарных функций),
тогда
-
целая рациональная функция
(смотритеклассификацию
элементарных функций),
тогда ![]() .
.
В
свою очередь, g(x) также
может быть сложной функцией. Например,  .
Условно такое выражение можно обозначить
как
.
Условно такое выражение можно обозначить
как![]() .
Здесьf –
функция синуса,
.
Здесьf –
функция синуса, ![]() -
функция извлечения квадратного корня,
-
функция извлечения квадратного корня,![]() -
дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
-
дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом![]() .
.
Часто можно слышать, что сложную функцию называют композицией функций.
Формула
нахождения производной сложной функции.
![]()
Пример.
Найти
производную сложной функции ![]() .
.
Решение.
В данном примере f – функция возведения в квадрат, а g(x) = 2x+1 – линейная функция.
Вот
подробное решение с использованием
формулы производной сложной функции:
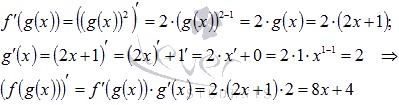
Давайте
найдем эту производную, предварительно
упростив вид исходной функции.
![]()
Следовательно,
![]()
Как видите, результаты совпадают.
Постарайтесь не путать, какая функция есть f, а какая g(x).
Поясним это примером на внимательность.
Пример.
Найти
производные сложных функций ![]() и
и![]() .
.
Решение.
В
первом случае f –
это функция возведения в квадрат,
а g(x) –
функция синуса, поэтому
![]() .
.
Во
втором случае f –
это функция синуса, а ![]() -
степенная функция. Следовательно, по
формуле произведения сложной функции
имеем
-
степенная функция. Следовательно, по
формуле произведения сложной функции
имеем![]()
Формула
производной для функции ![]() имеет
вид
имеет
вид
Пример.
Продифференцировать
функцию ![]() .
.
Решение.
В
этом примере сложную функцию можно
условно записать как ![]() ,
где
,
где![]() -
функция синуса, функция возведения в
третью степень, функция логарифмирования
по основаниюe,
функция взятия арктангенса и линейная
функция соответственноПо формуле
производной сложной функции
-
функция синуса, функция возведения в
третью степень, функция логарифмирования
по основаниюe,
функция взятия арктангенса и линейная
функция соответственноПо формуле
производной сложной функции

Теперь находим
 как
производную синуса из таблицы
производных:
как
производную синуса из таблицы
производных:

 -
как производную степенной функции:
-
как производную степенной функции:
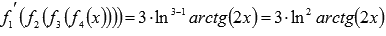
 -
как производную логарифмической
функции:
-
как производную логарифмической
функции:

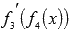 -
как производную арктангенса:
-
как производную арктангенса:

При дифференцировании
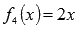 выносим
двойку за знак производной и применяем
формулу производной степенной функции
с показателем равным единице:
выносим
двойку за знак производной и применяем
формулу производной степенной функции
с показателем равным единице:
Собираем
воедино полученные промежуточные
результаты:

