Нормальное уравнение плоскости.

Общее уравнение плоскости вида называют нормальным уравнением плоскости, если длина вектора равна единице, то есть, , и .

Часто можно видеть, что нормальное уравнение плоскости записывают в виде . Здесь - направляющие косинусы нормального вектора данной плоскости единичной длины, то есть , а p – неотрицательное число, равное расстоянию от начала координат до плоскости.

Нормальное уравнение плоскости в прямоугольной системе координат Oxyz определяет плоскость, которая удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости . Если p=0, то плоскость проходит через начало координат.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида . Это общее уравнение плоскости является нормальным уравнением плоскости. Действительно, и нормальный вектор этой плоскости имеет длину равную единице, так как .

Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости.

7. Расстояние от точки до плоскости.

Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.

• Отклонение точки от плоскости заданной нормированным уравнением

,если и начало координат лежат по разные стороны плоскости, в противоположном случае. Расстояние от точки до плоскости равно

• Расстояние от точки, до плоскости, заданной уравнением, вычисляется по формуле:

8. Взаимное расположение плоскостей. Условия параллельности и перпендикулярности плоскостей.

Расстояние между параллельными плоскостями

• Расстояние между плоскостями, заданными уравнениями и:

• Расстояние между плоскостями, заданными уравнениями и:

Связанные понятия

• Плоскости параллельны, если

 или (Векторное произведение)

• Плоскости перпендикулярны, если

 или . (Скалярное произведение)

9. Прямая в пространстве. Различные виды уравнения прямой.

Уравнения прямой в пространстве – начальные сведения.

Уравнение прямой на плоскости в прямоугольной системе координат Oxy представляет собой линейное уравнение с двумя переменными x и y, которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. С прямой в трехмерном пространстве дело обстоит немного иначе – не существует линейного уравнения с тремя переменными x, y и z, которому бы удовлетворяли только координаты точек прямой, заданной в прямоугольной системе координат Oxyz. Действительно, уравнение вида , гдеx, y и z – переменные, а A, B, C и D – некоторые действительные числа, причем А, В и С одновременно не равны нулю, представляет собой общее уравнение плоскости. Тогда встает вопрос: «Каким же образом можно описать прямую линию в прямоугольной системе координат Oxyz»?

Ответ на него содержится в следующих пунктах статьи.

Уравнения прямой в пространстве - это уравнения двух пересекающихся плоскостей.

Напомним одну аксиому: если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. Таким образом, прямую линию в пространстве можно задать, указав две плоскости, пересекающиеся по этой прямой.

Переведем последнее утверждение на язык алгебры.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и известно, что прямая a является линией пересечения двух плоскостей и, которым отвечают общие уравнения плоскости видаисоответственно. Так как прямаяa представляет собой множество всех общих точек плоскостей и, то координаты любой точки прямой a будут удовлетворять одновременно и уравнениюи уравнению, координаты никаких других точек не будут удовлетворять одновременно обоим уравнениям плоскостей. Следовательно, координаты любой точки прямойa в прямоугольной системе координат Oxyz представляют собой частное решение системы линейных уравнений вида , а общее решение системы уравненийопределяет координаты каждой точки прямойa, то есть, определяет прямую a.

Итак, прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей .

Вот пример задания прямой линии в пространстве с помощью системы двух уравнений - .

Описание прямой линии уравнениями двух пересекающихся плоскостей отлично подходит принахождении координат точки пересечения прямой и плоскости, а также при нахождении координат точки пересечения двух прямых в пространстве.

Рекомендуем продолжить изучение этой темы, обратившись к статье уравнения прямой в пространстве - уравнения двух пересекающихся плоскостей. В ней дана более детальная информация, подробно разобраны решения характерных примеров и задач, а также показан способ перехода к уравнениям прямой в пространстве другого вида.

Следует отметить, что существуют различные способы задания прямой в пространстве, и на практике прямая чаще задается не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, лежащей на этой прямой. В этих случаях проще получить канонические и параметрические уравнения прямой в пространстве. О них поговорим в следующих пунктах.

Параметрические уравнения прямой в пространстве.

Параметрические уравнения прямой в пространстве имеют вид ,

где x₁,y₁ и z₁ – координаты некоторой точки прямой, a_x, a_y и a_z (a_x, a_y и a_z одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а - некоторый параметр, который может принимать любые действительные значения.

При любом значении параметра по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел,

она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при 

из параметрических уравнений прямой в пространстве получаем координаты x₁, y₁ и z₁: .

В качестве примера рассмотрим прямую, которую задают параметрические уравнения вида . Эта прямая проходит через точку, а направляющий вектор этой прямой имеет координаты.

Рекомендуем продолжить изучение темы, обратившись к материалу статьи параметрические уравнения прямой в пространстве. В ней показан вывод параметрических уравнений прямой в пространстве, разобраны частные случаи параметрических уравнений прямой в пространстве, даны графические иллюстрации, приведены развернутые решения характерных задач и указана связь параметрических уравнений прямой с другими видами уравнений прямой.

Канонические уравнения прямой в пространстве.

Разрешив каждое из параметрических уравнений прямой вида относительно параметра, легко перейти кканоническим уравнениям прямой в пространстве вида .

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку, а направляющим вектором прямой является вектор. К примеру, уравнения прямой в каноническом виде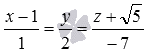соответствуют прямой, проходящей через точку пространства с координатами, направляющий вектор этой прямой имеет координаты.

Следует отметить, что одно или два из чисел в канонических уравнениях прямой могут быть равны нулю (все три числаодновременно не могут быть равны нулю, так как направляющий вектор прямой не может быть нулевым). Тогда запись видасчитается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как, где.

Если одно из чисел в канонических уравнениях прямой равно нулю, то прямая лежит в одной из координатных плоскостей, либо в плоскости ей параллельной. Если два из чиселравны нулю, то прямая либо совпадает с одной из координатных осей, либо параллельна ей. Например прямая, соответствующая каноническим уравнениям прямой в пространстве вида, лежит в плоскостиz=-2, которая параллельна координатной плоскости Oxy, а координатная ось Oy определяется каноническими уравнениями .

Графические иллюстрации этих случаев, вывод канонических уравнений прямой в пространстве, подробные решения характерных примеров и задач, а также переход от канонических уравнений прямой к другим уравнениям прямой в пространстве смотрите в статье канонические уравнения прямой в пространстве.

10. Общее уравнение прямой. Переход от общего к каноническому уравнению.