
- •Свойства
- •[Править]Неравенство Коши — Буняковского
- •Нормальное уравнение плоскости.
- •Общее уравнение прямой - основные сведения.
- •Переход от общего уравнения прямой
- •13,14,15,16 В отдельном файле
- •17. Цилиндрические поверхности с образующей, параллельной одной из координатных осей.
- •18. Матрицы. Линейные операции над матрицами, их свойства.
- •19. Нелинейные операции над матрицами (умножение, транспонирование), их свойства. Умножение матриц
- •Транспонирование и эрмитово сопряжение
- •20. Обратная матрица. Теорема существования, единственность, свойства.
- •21. Матричные уравнения. Теорема существования и единственности решения.
- •22. Решение системы линейных уравнений матричным методом. Правило Крамера.
- •23. Ранг матрицы. Свойства ранга.
- •24. Линейная зависимость столбцов матрицы. Свойства Линейная зависимость и независимость строк (столбцов) матрицы
- •Свойства линейно зависимых и линейно независимых столбцов матриц
- •25. Базисный минор. Теорема о базисном миноре. Теорема о ранге.
- •26. Системы линейных уравнений. Теорема Кронекера - Капелли о совместимости систем.
- •27. Однородные системы линейных уравнений. Свойства их решений. Общее решение ослу.
- •28. Фундаментальная система решений ослу
- •29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
- •30. Линейные пространства. Определение. Примеры, следствия из аксиом.
- •31. Линейная зависимость векторов линейного пространства. Свойства
- •32. Базис линейного пространства. Размерность
- •33. Единственность разложения векторов по базису. Координаты. Действия над векторами в координатной форме.
- •34. Изменение координат вектора при переходе к новому базису. Матрица перехода.
- •35. Евклидово пространство. Определение, примеры. Модуль вектора. Угол между векторами. Неравенство Коши-Буняковского.
- •36. Линейный оператор. Матрица линейного оператора. Изменение матрицы линейного оператора при переходе к новому базису.
- •37. Образ и ядро линейного оператора. Ранг линейного оператора.
- •38.В отдельном файле.
- •39. Собственные векторы и собственные значения линейного оператора. Их свойства
- •40. Последовательность. Предел последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. Определение
- •[Править]Примеры
- •[Править]Операции над последовательностями
- •[Править]Подпоследовательности
- •[Править]Примеры
- •[Править]Свойства
- •[Править]Предельная точка последовательности
- •[Править]Предел последовательности
- •[Править]Некоторые виды последовательностей
- •[Править]Ограниченные и неограниченные последовательности
- •[Править]Критерий ограниченности числовой последовательности
- •[Править]Свойства ограниченных последовательностей
- •[Править]Бесконечно большие и бесконечно малые последовательности
- •[Править]Свойства бесконечно малых последовательностей
- •[Править]Сходящиеся и расходящиеся последовательности
- •[Править]Свойства сходящихся последовательностей
- •41. Понятие функции. Способы задания функции.
- •42. Предел функции в точке, в бесконечности. Геометрическая интерпретация. Определения и примеры.
- •43. Теоремы о пределах:
- •44. Непрерывные функции и их свойства:
- •Свойства Локальные
- •Глобальные
- •Теорема о сохранении знака для непрерывной функции
- •Доказательство
- •45. Первый замечательный предел. Следствия. Теорема о пределе суммы, произведения и частного.
- •46. Ограниченные функции и их свойства. Необходимое условие существования предела функции в точке.
- •47. Бесконечно малые функции, их свойства. Леммы
- •Леммы о бесконечно малых
- •48. Критерий существования предела функции в точке.
- •49. Бесконечно большие функции, связь с бесконечно малыми функциями.
- •50. Раскрытие неопределенностей. Второй замечательный предел.
- •51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
- •52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
- •3.2. Основные формулы эквивалентности бесконечно малых.
- •53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
- •54. Точки разрыва функции и их классификация.
- •55. Свойства функций, непрерывных на отрезке.
- •56. Задачи, приводящие к понятию производной. Понятие производной. Геометрический и физический смысл производной.
- •1.1 Задачи, приводящие к понятию производной
- •, Если .
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •57. Дифференцируемость функции. Критерий дифференцируемости функции в точке.
- •58. Производная сложной функции.
- •59. Дифференциал функции. Инвариантность формы записи первого дифференциала.
- •60. Обратная функция и ее производная.
- •60. Обратная функция и ее производная.
- •61. Правила дифференцирования.
- •63. Логарифмическое дифференцирование. Производная степенно-показательной функции.
- •5.4. Производная степенно-показательной функции
- •64. См. Отдельный файл.
- •65. Теоремы о среднем – Ферма, Ролля.
- •66. Теоремы о среднем – Лагранжа, Коши.
- •67. Дифференциалы высших порядков. Неинвариантность формы записи.
- •68. Правило Лопиталя. Раскрытие неопределенностей с использованием правила Лопиталя.
- •69. Формула Тейлора. Разложение функции по формуле Тейлора.
- •70. Монотонность функции. Условия монотонности.
- •71. Экстремумы функции. Необходимое условие существования экстремума.
- •72. Достаточные условия экстремума.
- •73. Выпуклость и вогнутость графика функции. Точки перегиба.
- •74. Асимптоты графика.
- •[Править]Виды асимптот графиков [править]Вертикальная
- •[Править]Горизонтальная
- •[Править]Наклонная
- •[Править]Нахождение асимптот
- •76. Метод замены переменных в неопределенном интеграле.
- •77. Интегрирование по частям в неопределенном интеграле. Классы функций, интегрируемых по частям.
- •78. Рациональные дроби. Разложение рациональных дробей на сумму простейших.
- •79. Интегрирование простейших рациональных дробей.
- •80. Интегрирование тригонометрических функций.
- •81. Интегрирование иррациональностей вида…
- •82. Интегрирование иррациональностей вида…
- •83. Понятие определенного интеграла, его геометрический смысл и свойства. Теорема о среднем.
- •84. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •85. Полярная система координат. Уравнения кривых в полярной системе координат.
- •Уравнение кривых в полярных координатах
- •Окружность
- •Полярная роза
- •Спираль Архимеда
- •Конические сечения
- •86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
- •87. Вычисление объемов тел, объемов тел вращения.
- •88. Приложение определенного интеграла к задачам физики.
- •89. Несобственные интегралы I рода.
- •89. Несобственные интегралы I рода.
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •90. Несобственные интегралы II рода.
- •Геометрический смысл несобственных интегралов II рода
30. Линейные пространства. Определение. Примеры, следствия из аксиом.
Аксиомы линейного пространства
Линейным
(векторным) пространством
называется множество ![]() произвольных
элементов, называемых векторами, в
котором определены операции сложения
векторов и умножения вектора на число,
т.е. любым двум векторам
произвольных
элементов, называемых векторами, в
котором определены операции сложения
векторов и умножения вектора на число,
т.е. любым двум векторам![]() и
и![]() поставлен
в соответствие вектор
поставлен
в соответствие вектор![]() ,
называемый суммой векторов
,
называемый суммой векторов![]() и
и![]() ,
любому вектору
,
любому вектору![]() и
любому числу
и
любому числу![]() из
поля действительных чисел
из
поля действительных чисел![]() поставлен
в соответствие вектор
поставлен
в соответствие вектор![]() ,
называемый произведением вектора
,
называемый произведением вектора![]() на
число
на
число![]() ;
так что выполняются следующие условия:
;
так что выполняются следующие условия:
1. ![]() (коммутативность
сложения);
(коммутативность
сложения);
2. ![]() (ассоциативность
сложения);
(ассоциативность
сложения);
3. существует
такой элемент ![]() ,
называемый нулевым вектором, что
,
называемый нулевым вектором, что![]() ;
;
4. для
каждого вектора ![]() существует
такой вектор
существует
такой вектор![]() ,
называемый противоположным вектору
,
называемый противоположным вектору![]() ,
что
,
что![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ;
;
8. ![]() .
.
Условия
1-8 называются аксиомами
линейного пространства.
Знак равенства, поставленный между
векторами, означает, что в левой и правой
частях равенства представлен один и
тот же элемент множества ![]() ,
такие векторы называются равными.
,
такие векторы называются равными.
В
определении линейного пространства
операция умножения вектора на число
введена для действительных чисел. Такое
пространство называютлинейным
пространством над полем действительных
(вещественных) чисел,
или, короче, вещественным
линейным пространством.
Если в определении вместо поля ![]() действительных
чисел взять поле комплексных чисел
действительных
чисел взять поле комплексных чисел![]() ,
то получимлинейное
пространство над полем комплексных
чисел,
или, короче, комплексное
линейное пространство.
В качестве числового поля можно выбрать
и поле
,
то получимлинейное
пространство над полем комплексных
чисел,
или, короче, комплексное
линейное пространство.
В качестве числового поля можно выбрать
и поле ![]() рациональных
чисел, при этом получим линейное
пространство над полем рациональных
чисел. Далее, если не оговорено противное,
будут рассматриваться вещественные
линейные пространства. В некоторых
случаях для краткости будем говорить
о пространстве, опуская слово линейное,
так как все пространства, рассматриваемые
ниже — линейные.
рациональных
чисел, при этом получим линейное
пространство над полем рациональных
чисел. Далее, если не оговорено противное,
будут рассматриваться вещественные
линейные пространства. В некоторых
случаях для краткости будем говорить
о пространстве, опуская слово линейное,
так как все пространства, рассматриваемые
ниже — линейные.
Замечания 8.1
1. Аксиомы 1-4 показывают, что линейное пространство является коммутативной группой относительно операции сложения.
2. Аксиомы 5 и 6 определяют дистрибутивность операции умножения вектора на число по отношению к операции сложения векторов (аксиома 5) или к операции сложения чисел (аксиома 6). Аксиома 7, иногда называемая законом ассоциативности умножения на число, выражает связь двух разных операций: умножения вектора на число и умножения чисел. Свойство, определяемое аксиомой 8, называется унитарностью операции умножения вектора на число.
3. Линейное пространство — это непустое множество, так как обязательно содержит нулевой вектор.
4. Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами.
5. Разностью
векторов ![]() и
и![]() называется
сумма вектора
называется
сумма вектора![]() с
противоположным вектором
с
противоположным вектором![]() и
обозначается:
и
обозначается:![]() .
.
6. Два
ненулевых вектора ![]() и
и![]() называются
коллинеарными (пропорциональными), если
существует такое число
называются
коллинеарными (пропорциональными), если
существует такое число![]() ,
что
,
что![]() .
Понятие коллинеарности распространяется
на любое конечное число векторов. Нулевой
вектор
.
Понятие коллинеарности распространяется
на любое конечное число векторов. Нулевой
вектор![]() считается
коллинеарным с любым вектором.
считается
коллинеарным с любым вектором.
Следствия аксиом линейного пространства
1. В линейном пространстве существует единственный нулевой вектор.
2.
В линейном пространстве для любого
вектора ![]() существует
единственный противоположный вектор
существует
единственный противоположный вектор![]() .
.
3.
Произведение произвольного вектора
пространства на число нуль равно нулевому
вектору, т.е. ![]() .
.
4.
Произведение нулевого вектора на любое
число равно нулевому вектору, т.е ![]() для
любого числа
для
любого числа![]() .
.
5.
Вектор, противоположный данному вектору,
равен произведению данного вектора на
число (-1), т.е. ![]() .
.
6.
В выражениях вида ![]() (сумма
конечного числа векторов) или
(сумма
конечного числа векторов) или![]() (произведение
вектора на конечное число множителей)
можно расставлять скобки в любом порядке,
либо вообще не указывать.
(произведение
вектора на конечное число множителей)
можно расставлять скобки в любом порядке,
либо вообще не указывать.
Докажем,
например, первые два свойства.
Единственность нулевого вектора.
Если ![]() и
и![]() —
два нулевых вектора, то по аксиоме 3
получаем два равенства:
—
два нулевых вектора, то по аксиоме 3
получаем два равенства:![]() или
или![]() ,
левые части которых равны по аксиоме
1. Следовательно, равны и правые части,
т.е.
,
левые части которых равны по аксиоме
1. Следовательно, равны и правые части,
т.е.![]() .
Единственность противоположного
вектора. Если вектор
.
Единственность противоположного
вектора. Если вектор![]() имеет
два противоположных вектора
имеет
два противоположных вектора![]() и
и![]() ,
то по аксиомам 2, 3,4 получаем их равенство:
,
то по аксиомам 2, 3,4 получаем их равенство:
![]()
Остальные свойства доказываются аналогично.
Примеры линейных пространств
1.
Обозначим ![]() —
множество, содержащее один нулевой
вектор, с операциями
—
множество, содержащее один нулевой
вектор, с операциями![]() и
и![]() .
Для указанных операций аксиомы 1-8
выполняются. Следовательно,
множество
.
Для указанных операций аксиомы 1-8
выполняются. Следовательно,
множество![]() является
линейным пространством над любым
числовым полем. Это линейное пространство
называется нулевым.
является
линейным пространством над любым
числовым полем. Это линейное пространство
называется нулевым.
2.
Обозначим ![]() —
множества векторов (направленных
отрезков) на прямой, на плоскости, в
пространстве соответственно с обычными
операциями сложения векторов и умножения
векторов на число. Выполнение аксиом
1-8 линейного пространства следует из
курса элементарной геометрии.
Следовательно, множества
—
множества векторов (направленных
отрезков) на прямой, на плоскости, в
пространстве соответственно с обычными
операциями сложения векторов и умножения
векторов на число. Выполнение аксиом
1-8 линейного пространства следует из
курса элементарной геометрии.
Следовательно, множества![]() являются
вещественными линейными пространствами.
Вместо свободных векторов можно
рассмотреть соответствующие множества
радиус-векторов. Например, множество
векторов на плоскости, имеющих общее
начало, т.е. отложенных от одной
фиксированной точки плоскости, является
вещественным линейным пространством.
Множество радиус-векторов единичной
длины не образует линейное пространство,
так как для любого из этих векторов
сумма
являются
вещественными линейными пространствами.
Вместо свободных векторов можно
рассмотреть соответствующие множества
радиус-векторов. Например, множество
векторов на плоскости, имеющих общее
начало, т.е. отложенных от одной
фиксированной точки плоскости, является
вещественным линейным пространством.
Множество радиус-векторов единичной
длины не образует линейное пространство,
так как для любого из этих векторов
сумма![]() не
принадлежит рассматриваемому множеству.
не
принадлежит рассматриваемому множеству.
3.
Обозначим ![]() —
множество матриц-столбцов размеров
—
множество матриц-столбцов размеров![]() с
операциями сложения матриц и умножения
матриц на число. Аксиомы 1-8 линейного
пространства для этого множества
выполняются. Нулевым вектором в этом
множестве служит нулевой столбец
с
операциями сложения матриц и умножения
матриц на число. Аксиомы 1-8 линейного
пространства для этого множества
выполняются. Нулевым вектором в этом
множестве служит нулевой столбец![]() .
Следовательно, множество
.
Следовательно, множество![]() является
вещественным линейным пространством.
Аналогично, множество
является
вещественным линейным пространством.
Аналогично, множество![]() столбцов
размеров
столбцов
размеров![]() с
комплексными элементами является
комплексным линейным пространством.
Множество матриц-столбцов с неотрицательными
действительными элементами, напротив,
не является линейным пространством,
так как не содержит противоположных
векторов.
с
комплексными элементами является
комплексным линейным пространством.
Множество матриц-столбцов с неотрицательными
действительными элементами, напротив,
не является линейным пространством,
так как не содержит противоположных
векторов.
4.
Обозначим ![]() —
множество решений однородной
системы
—
множество решений однородной
системы![]() линейных
алгебраических уравнений с и неизвестными
(где
линейных
алгебраических уравнений с и неизвестными
(где![]() —
действительная матрица системы),
рассматриваемое как множество столбцов
размеров
—
действительная матрица системы),
рассматриваемое как множество столбцов
размеров![]() с
операциями сложения матриц и умножения
матриц на число. Заметим, что эти операции
действительно определены на множестве
с
операциями сложения матриц и умножения
матриц на число. Заметим, что эти операции
действительно определены на множестве![]() .
Из свойства 1 решений однородной системы
(см. разд. 5.5) следует, что сумма двух
решений однородной системы и произведение
ее решения на число также являются
решениями однородной системы, т.е.
принадлежат множеству
.
Из свойства 1 решений однородной системы
(см. разд. 5.5) следует, что сумма двух
решений однородной системы и произведение
ее решения на число также являются
решениями однородной системы, т.е.
принадлежат множеству![]() .
Аксиомы линейного пространства для
столбцов выполняются (см. пункт 3 в
примерах линейных пространств). Поэтому
множество решений однородной системы
является вещественным линейным
пространством.
.
Аксиомы линейного пространства для
столбцов выполняются (см. пункт 3 в
примерах линейных пространств). Поэтому
множество решений однородной системы
является вещественным линейным
пространством.
Множество ![]() решений
неоднородной системы
решений
неоднородной системы![]() ,
напротив, не является линейным
пространством, хотя бы потому, что не
содержит нулевого элемента (
,
напротив, не является линейным
пространством, хотя бы потому, что не
содержит нулевого элемента (![]() не
является решением неоднородной системы).
не
является решением неоднородной системы).
5.
Обозначим ![]() —
множество матриц размеров
—
множество матриц размеров![]() с
операциями сложения матриц и умножения
матриц на число. Аксиомы 1-8 линейного
пространства для этого множества
выполняются. Нулевым вектором является
нулевая матрица
с
операциями сложения матриц и умножения
матриц на число. Аксиомы 1-8 линейного
пространства для этого множества
выполняются. Нулевым вектором является
нулевая матрица![]() соответствующих
размеров. Следовательно, множество
соответствующих
размеров. Следовательно, множество![]() является
линейным пространством.
является
линейным пространством.
6.
Обозначим ![]() —
множество многочленов одной переменной
с комплексными коэффициентами. Операции
сложения много членов и умножения
многочлена на число, рассматриваемое
как многочлен нулевой степени, определены
и удовлетворяют аксиомам 1-8 (в частности,
нулевым вектором является многочлен,
тождественно равный нулю). Поэтому
множество
—
множество многочленов одной переменной
с комплексными коэффициентами. Операции
сложения много членов и умножения
многочлена на число, рассматриваемое
как многочлен нулевой степени, определены
и удовлетворяют аксиомам 1-8 (в частности,
нулевым вектором является многочлен,
тождественно равный нулю). Поэтому
множество![]() является
линейным пространством над полем
комплексных чисел. Множество
является
линейным пространством над полем
комплексных чисел. Множество![]() многочленов
с действительными коэффициентами также
является линейным пространством (но,
разумеется, над полем действительных
чисел). Множество
многочленов
с действительными коэффициентами также
является линейным пространством (но,
разумеется, над полем действительных
чисел). Множество![]() многочленов
степени не выше, чем
многочленов
степени не выше, чем![]() ,
с действительными коэффициентами также
является вещественным линейным
пространством. Заметим, что операция
сложения много членов определена на
этом множестве, так как степень суммы
многочленов не превышает степеней
слагаемых.
,
с действительными коэффициентами также
является вещественным линейным
пространством. Заметим, что операция
сложения много членов определена на
этом множестве, так как степень суммы
многочленов не превышает степеней
слагаемых.
Множество
многочленов степени ![]() не
является линейным пространством, так
как сумма таких многочленов может
оказаться многочленом меньшей степени,
не принадлежащим рассматриваемому
множеству. Множество всех многочленов
степени не выше, чем л, с положительными
коэффициентами также не является
линейным пространством, поскольку при
умножении такого многочлена на
отрицательное число получим многочлен,
не принадлежащий этому множеству.
не
является линейным пространством, так
как сумма таких многочленов может
оказаться многочленом меньшей степени,
не принадлежащим рассматриваемому
множеству. Множество всех многочленов
степени не выше, чем л, с положительными
коэффициентами также не является
линейным пространством, поскольку при
умножении такого многочлена на
отрицательное число получим многочлен,
не принадлежащий этому множеству.
7.
Обозначим ![]() —
множество действительных функций,
определенных и непрерывных на
—
множество действительных функций,
определенных и непрерывных на![]() .
Сумма
.
Сумма![]() функций
функций![]() и
произведение
и
произведение![]() функции
функции![]() на
действительное число
на
действительное число![]() определяются
равенствами:
определяются
равенствами:
![]() для
всех
для
всех ![]()
Эти
операции действительно определены
на ![]() ,
так как сумма непрерывных функций и
произведение непрерывной функции на
число являются непрерывными функциями,
т.е. элементами
,
так как сумма непрерывных функций и
произведение непрерывной функции на
число являются непрерывными функциями,
т.е. элементами![]() .
Проверим выполнение аксиом линейного
пространства. Из коммутативности
сложения действительных чисел следует
справедливость равенства
.
Проверим выполнение аксиом линейного
пространства. Из коммутативности
сложения действительных чисел следует
справедливость равенства![]() для
любого
для
любого![]() .
По этому
.
По этому![]() ,
т.е. аксиома 1 выполняется. Аксиома 2
следует аналогично из ассоциативности
сложения. Нулевым вектором служит
функция
,
т.е. аксиома 1 выполняется. Аксиома 2
следует аналогично из ассоциативности
сложения. Нулевым вектором служит
функция![]() ,
тождественно равная нулю, которая,
разумеется, является непрерывной. Для
любой функции
,
тождественно равная нулю, которая,
разумеется, является непрерывной. Для
любой функции![]() выполняется
равенство
выполняется
равенство![]() ,
т.е. справедлива аксиома 3. Противоположным
вектором для вектора
,
т.е. справедлива аксиома 3. Противоположным
вектором для вектора![]() будет
функция
будет
функция![]() .
Тогда
.
Тогда![]() (аксиома
4 выполняется). Аксиомы 5, 6 следуют из
дистрибутивности операций сложения и
умножения действительных чисел, а
аксиома 7 — из ассоциативности умножения
чисел. Последняя аксиома выполняется,
так как умножение на единицу не изменяет
функцию:
(аксиома
4 выполняется). Аксиомы 5, 6 следуют из
дистрибутивности операций сложения и
умножения действительных чисел, а
аксиома 7 — из ассоциативности умножения
чисел. Последняя аксиома выполняется,
так как умножение на единицу не изменяет
функцию:![]() для
любого
для
любого![]() ,
т.е.
,
т.е.![]() .
Таким образом, рассматриваемое
множество
.
Таким образом, рассматриваемое
множество![]() с
введенными операциями является
вещественным линейным пространством.
Аналогично доказывается, что
с
введенными операциями является
вещественным линейным пространством.
Аналогично доказывается, что![]() —
множества функций, имеющих непрерывные
производные первого, второго .и т.д.
порядков соответственно, также являются
линейными пространствами.
—
множества функций, имеющих непрерывные
производные первого, второго .и т.д.
порядков соответственно, также являются
линейными пространствами.
Обозначим ![]() —
множество тригонометрических двучленов
(часто ты
—
множество тригонометрических двучленов
(часто ты![]() )
с действительными коэффициентами, т.е.
множество функций вида
)
с действительными коэффициентами, т.е.
множество функций вида![]() ,
где
,
где![]() .
Сумма таких двучленов и про изведение
двучлена на действительное число
являются тригонометрическим двучленом.
Аксиомы линейного пространства для
рассматриваемого множества выполняются
(так как
.
Сумма таких двучленов и про изведение
двучлена на действительное число
являются тригонометрическим двучленом.
Аксиомы линейного пространства для
рассматриваемого множества выполняются
(так как![]() ).
Поэтому множество
).
Поэтому множество![]() с
обычными для функций операциями сложения
и умножения на число является вещественным
линейным пространством. Нулевым элементом
служит двучлен
с
обычными для функций операциями сложения
и умножения на число является вещественным
линейным пространством. Нулевым элементом
служит двучлен![]() ,
тождественно равный нулю.
,
тождественно равный нулю.
Множество
действительных функций, определенных
и монотонных на ![]() ,
не является линейным пространством,
так как разность двух монотонных функций
может оказаться немонотонной функцией.
,
не является линейным пространством,
так как разность двух монотонных функций
может оказаться немонотонной функцией.
8.
Обозначим ![]() —
множество действительных функций,
определенных на множестве
—
множество действительных функций,
определенных на множестве![]() ,
с операциями:
,
с операциями:
![]()
Оно
является вещественным линейным
пространтвом (доказательство такое же,
как в предыдущем примере). При этом
множество ![]() может
быть выбрано произвольно. В частности,
если
может
быть выбрано произвольно. В частности,
если![]() ,
то
,
то![]() —
упорядоченный набор чисел
—
упорядоченный набор чисел![]() ,
где
,
где![]() Такой
набор можно считать матрицей-столбцом
размеров
Такой
набор можно считать матрицей-столбцом
размеров![]() ,
т.е. множество
,
т.е. множество![]() совпадает
с множеством
совпадает
с множеством![]() (см.
пункт 3 примеров линейных пространств).
Если
(см.
пункт 3 примеров линейных пространств).
Если![]() (напомним,
что
(напомним,
что![]() —
множество натуральных чисел), то получаем
линейное пространство
—
множество натуральных чисел), то получаем
линейное пространство![]() —
множество числовых последовательностей
—
множество числовых последовательностей![]() .
В частности, множество сходящихся
числовых последовательностей также
образует линейное пространство, так
как сумма двух сходящихся последовательностей
сходится, и при умножении всех членов
сходящейся последовательности на число
получаем сходящуюся последовательность.
Напротив, множество расходящихся
последовательностей не является линейным
пространством, так как, например, сумма
расходящихся последовательностей может
иметь предел.
.
В частности, множество сходящихся
числовых последовательностей также
образует линейное пространство, так
как сумма двух сходящихся последовательностей
сходится, и при умножении всех членов
сходящейся последовательности на число
получаем сходящуюся последовательность.
Напротив, множество расходящихся
последовательностей не является линейным
пространством, так как, например, сумма
расходящихся последовательностей может
иметь предел.
9.
Обозначим ![]() —
множество положительных действительных
чисел, в котором сумма
—
множество положительных действительных
чисел, в котором сумма![]() и
произведение
и
произведение![]() (обозначения
в этом примере отличаются от обычных)
определены равенствами:
(обозначения
в этом примере отличаются от обычных)
определены равенствами:![]() ,
другими словами, сумма элементов
понимается как произведение чисел, а
умножение элемента на число — как
возведение в степень. Обе операции
действительно определены на множестве
,
другими словами, сумма элементов
понимается как произведение чисел, а
умножение элемента на число — как
возведение в степень. Обе операции
действительно определены на множестве![]() ,
так как произведение положительных
чисел есть положительное число и любая
действительная степень положительного
числа есть положительное число. Проверим
справедливость аксиом. Равенства
,
так как произведение положительных
чисел есть положительное число и любая
действительная степень положительного
числа есть положительное число. Проверим
справедливость аксиом. Равенства
![]()
показывают,
что аксиомы 1, 2 выполняются. Нулевым
вектором данного множества является
единица, так как ![]() ,
т.е.
,
т.е.![]() .
Противоположным для
.
Противоположным для![]() вектором
является вектор
вектором
является вектор![]() ,
который определен, так как
,
который определен, так как![]() .
В самом деле,
.
В самом деле,![]() .
Проверим выполнение аксиом 5, 6,7,8:
.
Проверим выполнение аксиом 5, 6,7,8:
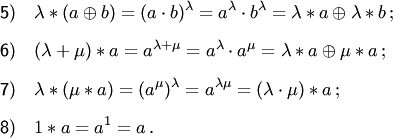 Все
аксиомы выполняются. Следовательно,
рассматриваемое множество является
вещественным линейным пространством.
Все
аксиомы выполняются. Следовательно,
рассматриваемое множество является
вещественным линейным пространством.
10.
Пусть ![]() —
вещественное линейное пространство.
Рассмотрим множество определенных
на
—
вещественное линейное пространство.
Рассмотрим множество определенных
на![]() линейных
скалярных функций, т.е. функций
линейных
скалярных функций, т.е. функций![]() ,
принимающих действительные значения
и удовлетворяющих условиям:
,
принимающих действительные значения
и удовлетворяющих условиям:
![]() (аддитивность);
(аддитивность);
![]() (однородность).
(однородность).
Линейные
операции над линейными функциями
задаются также, как в пункте 8 примеров
линейных пространств. Сумма ![]() и
произведение
и
произведение![]() определяются
равенствами:
определяются
равенствами:
![]()
Выполнение
аксиом линейного пространства
подтверждается также, как в пункте 8.
Поэтому множество линейных функций,
определенных на линейном пространстве ![]() ,
является линейным пространством. Это
пространство называется сопряженным
к пространству
,
является линейным пространством. Это
пространство называется сопряженным
к пространству![]() и
обозначается
и
обозначается![]() .
Его элементы называют ковекторами.
.
Его элементы называют ковекторами.
Например,
множество линейных форм ![]() переменных,
рассматриваемых как множество скалярных
функций векторного аргумента, является
линейным пространством, сопряженным к
пространству
переменных,
рассматриваемых как множество скалярных
функций векторного аргумента, является
линейным пространством, сопряженным к
пространству![]() .
.
