28. Фундаментальная система решений ослу

Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с nнеизвестными переменными называют совокупность (n – r) линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы. Если обозначить линейно независимые решения однородной СЛАУ как X⁽¹⁾, X⁽²⁾, …, X^(n-r) (X⁽¹⁾, X⁽²⁾, …, X^(n-r) – это матрицы столбцы размерности n на 1), то общее решение этой однородной системы представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С₁, С₂, …, С_(n-r), то есть, . Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)? Смысл прост: формула задает все возможные решения исходной СЛАУ, другими словами, взяв любой набор значений произвольных постоянных С₁, С₂, …, С_(n-r), по формуле мы получим одно из решений исходной однородной СЛАУ. Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как . Покажем процесс построения фундаментальной системы решений однородной СЛАУ. Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения1, 0, 0, …, 0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X⁽¹⁾ - первое решение фундаментальной системы. Если придать свободным неизвестным значения 0, 1, 0, 0, …, 0 и вычислить при этом основные неизвестные, то получим X⁽²⁾. И так далее. Если свободным неизвестным переменным придадим значения0, 0, …, 0, 1 и вычислим основные неизвестные, то получим X^(n-r). Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде . Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде , где - общее решение соответствующей однородной системы, а - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0, 0, …, 0 и вычислив значения основных неизвестных. Разберем на примерах.  Пример. Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений . Решение. Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент a_{1 1} = 9 основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:   Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:   Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум. Базисным минором возьмем . Отметим для наглядности элементы системы, которые его образуют:   Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:   Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:   Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X⁽¹⁾ придадим свободным неизвестным переменным значения x₂ = 1, x₄ = 0, тогда основные неизвестные найдем из системы уравнений . Решим ее методом Крамера:  Таким образом, . Теперь построим X⁽²⁾. Для этого придадим свободным неизвестным переменным значения x₂ = 0, x₄ = 1, тогда основные неизвестные найдем из системы линейных уравнений . Опять воспользуемся методом Крамера:  Получаем 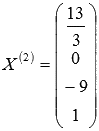. Так мы получили два вектора фундаментальной системы решений и , теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений: , где C₁ и C₂ – произвольные числа.