1. Определитель. Свойства. Способы вычисления.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определение через разложение по первой строке

схема расчета определителя матрицы .

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

Для матрицы определитель задаётся рекурсивно:

,    где —дополнительный минор к элементу . Эта формула называетсяразложением по строке.

В частности, формула вычисления определителя матрицы такова:

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Доказательство  [показать]

Также справедливо и аналогичное разложение по любой строке (столбцу):

Доказательство  [показать]

Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

Свойства определителей

• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , гдеи т. д. — строчки матрицы,— определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

2. Линейные операции над векторами, их свойства

Сложение векторов

Пусть даны два вектора и. Приложим векторк точке(концу вектора) и получим вектор(рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Векторназываетсясуммой векторов ии обозначается. Это нахождение суммы называетсяправилом треугольника.

Сумму двух неколлинеарных векторов иможно найти поправилу параллелограмма. Для этого откладываем от любой точки векторыи, а затем строим параллелограмм(рис. 1.7,6). Диагональпараллелограмма определяет сумму:

Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма четырех векторов. Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде , получим вектор, равный вектору. Если ломаная получилась замкнутой, то сумма равна нулевому вектору.

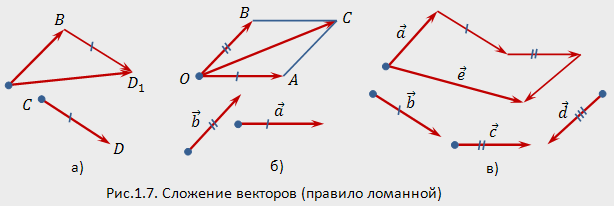
Вычитание векторов

Вектор называется противоположным вектору, если их сумма равна нулевому вектору:. Противоположный векторимеет длину, коллинеарен и противоположно направлен вектору(рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

Разностью векторов иназывается сумма векторас вектором, противоположным вектору:

Для нахождения разности векторов иприложим к произвольной точкевекторыи, а также вектор, противоположный вектору(рис.1.9,а). Искомую разность находим по правилу параллелограмма:

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке векторыи. Векторпри этом равен искомой разности

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов иназывается такой вектор, который в сумме с векторомдает вектор(рис.1.9,в), т.е. разность— это решение линейного векторного уравнения.

Пример 1.2. Для векторов, изображённых на рис. 1.6 (в конце), найти следующие суммы и разности:

Решение. Учитывая равенство , получаем по правилу треугольника.

Поскольку и, то.

По правилу параллелограмма . Так каки, находим

Умножение вектора на число

Произведением ненулевого вектора на действительное числоназывается вектор, удовлетворяющий условиям:

1) длина вектора равна, т.е.;

2) векторы иколлинеарные;

3) векторы иодинаково направлены, если, и противоположно направлены, если.

Произведение нулевого вектора на любое число считается (по определению) нулевым вектором:; произведение любого вектора на число нуль также считается нулевым вектором:. Из определения произведения следует, что

а) при умножении на единицу вектор не изменяется:;

б) при умножении вектора на получается противоположный вектор:;

в) деление вектора на отличное от нуля число сводится к его умножению на число, обратное.

г) при делении ненулевого вектора на его длину, т.е. при умножениина числополучаем единичный вектор, одинаково направленный с вектором.

Действительно, длина вектора равна единице:.

Вектор коллинеарен и одинаково направлен с вектором, так как;

д) при умножении единичного вектора на число получаем коллинеарный ему вектор, длина которого равна.

На рис.1.10 изображены векторы, получающиеся в результате умножения данного вектора наи, а также противоположный вектор.

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов ,,и любых действительных чиселсправедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

3. Скалярное произведение, свойства, вычисление в ДПСК

Скаля́рное произведе́ние (в зарубежной литературе - scalar product, dot product, inner product ) — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекциювектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:,,

Определение

Скалярным произведением в векторном пространстве надполем комплексных (или вещественных) чисел называется функция для элементов, принимающая значения в(или), определенная для каждой пары элементов и удовлетворяющая следующим условиям:

1. для любых трех элементов ипространства и любых чиселиз(или) справедливо равенство(линейность скалярного произведения по первому аргументу);

2. для любых исправедливо равенство, где черта означает комплексное сопряжение (эрмитова симметричность);

3. для любого имеем, причемтолько при(положительная определенность скалярного произведения).

Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.

Заметим, что из п.2 определения следует, что . Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значенияскалярного произведения.

Элементарное определение

A • B = |A| |B| cos(θ)

Элементарное определение скалярного произведения используется, когда определения длины вектора и угла между векторами введены независимым образом до введения понятия скалярного произведения (как правило, так и поступают при изложении элементарной геометрии). В этом случае скалярное произведение определяется через длины сомножителей и угол между ними:

Современная аксиоматика обычно строится начиная со скалярного произведения, и тогда длина вектора и угол определяются уже через скалярное произведение (см. ниже).

Связанные определения

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:

• Длина вектора, под которой обычно понимается его евклидова норма: (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

• Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):     В случае, если пространство являетсяпсевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):     

• Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.

• Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.

  • При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.

• Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называетсяпсевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

Свойства

• теорема косинусов легко выводится с использованием скалярного произведения:

• Угол между векторами:

• Оценка угла между векторами:

в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

• Проекция вектора 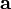на направление, определяемое единичным вектором :

,

• условие ортогональности^[2] (перпендикулярности) векторов и :

• Площадь параллелограмма, натянутого на два вектора и , равна

[Править]Неравенство Коши — Буняковского

Для любых элементов и линейного пространства со скалярным произведением выполняется неравенство [1]

С в о й с т в а   скалярного произведения

1.                =0, если

2.                , множители можно менять местами.

3.                

4.                

В ы ч и с л е н и е скалярного произведения в ДПСК.  Пусть векторы заданы координатами 

,

.

Учитывая свойства скалярного произведения, получаем

.

 

 

С учетом того, что

,

 получается

.                                                                  (7)

В частности

,

откуда

.                                                                        (8)

Как следует из выражения (4), скалярное произведение равно сумме произведений соответствующих координат. С помощью выражений (5) и (6) получаем

.                                                    (9)

П р и м е р. Найдите скалярное произведение векторов и косинус угла между ними.

Р е ш е н и е. Подставляем координаты векторов в формулу (4) и получаем значение скалярного произведения

С помощью формулы (9) находим косинус угла между векторами

.

4. Векторное произведение, свойства, вычисление в ДПСК

Векторное произведение векторов

 

О п р е д е л е н и е. Векторным произведением иназывается вектор, удовлетворяющий следующим условиям

1.                .

2.                .

3.                Векторы образуют правую тройку векторов.

Векторное произведение символически обозначается

.

Свойства векторного произведения

1.                ,

2.                ,

3.                

4.                Векторное произведение по абсолютной величине равно площади параллелограмма, построенного на этих векторах как на составляющих   

Вычисление векторного произведения в ДПСК.  Пусть векторы заданы координатами 

,

.

Учитывая свойства векторного произведения, получаем

.

 

С учетом того, что

,

 получаем

                                               (10)

или

.                                                                       (11)

 

Векторное произведение в ДПСК согласно формуле (11) представляет собой символический определитель третьего порядка. Элементы первой строки – единичные векторы, элементы второй строки – координаты первого вектора, элементы третьей строки – координаты второго вектора.

5. Смешанное произведение, свойства, вычисление в ДПСК

Смешанное произведение 

О п р е д е л е н и е. Смешанным произведением трех векторов называется число, которое получается, если векторыиперемножить векторно и затем полученный вектор перемножить с векторомскалярно.

Геометрический смысл смешанного произведения

,   ,,,

.                                                        (12)

Если образуют правую тройку векторов, то смешанное произведение, если левую, то. Выражение (1) определяет объем параллелепипеда через векторы, на которых он построен как на составляющих. Значит,. Поэтому смешанное произведение указывают без указания знаков

.                                                                  (13)

Вычисление смешанного произведения в декартовых системах.  Векторное произведение

.

умножим на вектор скалярно

.                                (14)

Раскроем определитель по элементам третьей строки

.                                         (15)

Сравнивая правые части равенств (14) и (15), получаем

.                                                                  (16)

П р и м е р.  Найдите объём и высоту параллелепипеда, построенного на векторах

, если A(1;2;3),  B(2;1;4),   D(4;1;5), 

Р е ш е н и е. Введём обозначения . Подставляем координаты векторовв формулу (16)

.

Как известно, , откуда

.                                                                         (17)

Находим . Для этого вычисляем векторное произведение

,

находим модуль полученного вектора . Подставляем  значенияив формулу (17) и  получаем значение высоты

.

6. Плоскость, различные виды уравнения плоскости:

а) уравнение плоскости проходящей через заданную точку перпендикулярно заданному вектору;

б) общее уравнение плоскости;

в) уравнение плоскости в отрезках.

Уравнение плоскости – определение.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и задана плоскость.

Плоскость, как и любая другая геометрическая фигура, состоит из точек. В прямоугольной системе координат Oxyz каждой точке соответствует упорядоченная тройка чисел – координаты точки. Между координатами каждой точки плоскости можно установить зависимость с помощью уравнения, которое называют уравнением плоскости.

Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x, y и z, которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.

Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.

Осталось выяснить, какой вид имеет уравнение плоскости. Ответ на этот вопрос содержится в следующем пункте этой статьи. Забегая вперед, отметим, что уравнение плоскости может быть записано по-разному. Существование различных видов уравнения плоскости обусловлено спецификой решаемых задач.

К началу страницы

Общее уравнение плоскости.

Приведем формулировку теоремы, которая дает нам вид уравнения плоскости.

Теорема.

Всякое уравнение вида , гдеA, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида .

Уравнение называетсяобщим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.

Следует заметить, что уравнение вида , где- некоторое действительное число, отличное от нуля, будет определять ту же самую плоскость, так как равенстваиэквивалентны. К примеру, общие уравнения плоскостиизадают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.

Немного поясним смысл озвученной теоремы. В прямоугольной системе координат Oxyzкаждой плоскости соответствует ее уравнение общего вида , а каждому уравнениюсоответствует плоскость в заданной прямоугольной системе координат трехмерного пространства. Другими словами, плоскость и ее общее уравнение неразделимы.

Если все коэффициенты А, В, С и D в общем уравнении плоскости отличны от нуля, то оно называетсяполным. В противном случае, общее уравнение плоскости называется неполным.

Неполными уравнениями задаются плоскости, параллельные координатным осям, проходящие через координатные оси, параллельные координатным плоскостям, перпендикулярные координатным плоскостям, совпадающие с координатными плоскостями, а также плоскости, проходящие через начало координат.

Например, плоскость параллельна оси абсцисс и перпендикулярна координатной плоскостиOyz, уравнение z = 0 определяет координатную плоскость Oxy, а общее уравнение плоскости вида соответствует плоскости, проходящей через начало координат.

Отметим также, что коэффициенты A, B и C в общем уравнении плоскости представляют собойкоординаты нормального вектора плоскости.

Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.

Рекомендуем ознакомиться с материалом статьи общее уравнение плоскости, где информация по теме изложена детальнее, подробно разобраны решения характерных примеров и задач.

К началу страницы

Уравнение плоскости в отрезках.

Уравнение плоскости вида , гдеa, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках.

Такое название не случайно. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках . Для этого отмечаем точку, удаленную на5 единиц от начала координат в отрицательном направлении оси абсцисс, на 4 единицы в отрицательном направлении оси ординат и на 4 единицы в положительном направлении оси аппликат. Осталось соединить эти точки прямыми линиями. Плоскость полученного треугольника и есть плоскость, соответствующая уравнению плоскости в отрезках вида .

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках, там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.