Высшая математика (2 семестр) / otchet_k_l_r_po_matem_7_2 (1)

Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МЭИ» в г. Смоленске

Отчет по лабораторной работе № 7

Тема: Линейная алгебра

Студент	Зайцев Д.И.
Группа	ЭО-12
Преподаватель	Борисов А. В.

Смоленск 2012

Контрольные задания

Задание №1. Даны 2 вектора: , . Найти и угол  между этими векторами.

> with(linalg):

a:=([1,2,2,3]); b:=([3,1,5,1]);

> dotprod(a,b);

> phi=combine(angle(a,b));

Ответ: ,

Задание №2. Даны 3 вектора: , и . Найти: и .

> with(linalg):

> a:=([2,-3,1]); b:=([-3,1,2]); c:=([1,2,3]);

> m:=crossprod(a,b);

> n:=crossprod(b,c);

> crossprod(m,c);

> crossprod(a,n);

Ответ: ,

Задание №3. Даны системы векторов: 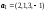, , 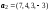, . Предварительно выяснив, является ли система базисом, применить процедуру ортогонализации Грамма-Шмидта и построить ортогональный базис этого подпространства.

> with(linalg):

> a1:=vector([2,1,3,-1]); a2:=vector([7,4,3,-3]); a3:=vector([1,1,-6,0]); a4:=vector([5,3,0,4]);

> g:=basis([a1,a2,a3,a4]);

> GramSchmidt(g);

Ответ: ,

Задание №4. Даны матрицы и . Найти: AB, BA, detA, detB.

> with(linalg): A:=matrix([[5,7,-3,-4],[7,6,-4,-5],[6,4,-3,-2],[8,5,-6,-1]]);

> B:=matrix([[1,2,3,4],[2,3,4,5],[1,3,5,7],[2,4,6,8]]);

> C:=evalm(A&*B);

> C:=evalm(B&*A);

> Det(A)=det(A);

> Det(B)=det(B);

Задание №5. Дана матрица: . Найти: detA, А^-1, M₃₂, A'.

> with(linalg):A:=matrix([[1,2,3,4],[2,3,1,2],[1,1,1,-1],[1,0,-2,-6]]);

> Det(A)=det(A);

> inverse(A);

> det(minor(A,3,2));

> transpose(A);

Задание №6. Найти ранг матрицы: . Привести матрицу С к треугольному виду.

> with(linalg): C:=matrix([[-6,4,8,-1,6],[-5,2,4,1,3],[7,2,4,1,3],[2,4,8,-7,6],[3,2,4,-5,3]]);

> r(C)=rank(C);

> g:=gausselim(C);

Задание №7. Дана матрица . Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной  в P_А () подставить А).

> with(linalg): A:=matrix([[5,4,3,2,1],[4,8,6,4,2],[3,6,9,6,3],[2,4,6,8,4],[1,2,3,4,5]]);

> eigenvalues(A);

> P(lambda):=charpoly(A,lambda);

> P(lambda):=charpoly(A,lambda);

> P(A)=evalm(A^5-35*A^4+336*A^3-1296*A^2+2160*A-1296);

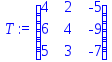
Задание №8. Дана матрица . Найти , det(), собственные векторы и собственные числа матрицы , ядро матрицы Т.

> with(linalg): T:=matrix([[4,2,-5],[6,4,-9],[5,3,-7]]);

> exponential(T);

> det(exponential(T));

> eigenvalues(exponential(T));

> eigenvectors(exponential(T));

> kernel(T);

Задание №9. Дана матрица . Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены.

> with(linalg):U:=matrix([[3,-4,0,2],[4,-5,-2,4],[0,0,3,-2],[0,0,2,-1]]);

> jordan(U);

> eigenvalues(U);

> eigenvectors(U);

> P(lambda):=charpoly(U,lambda);

> d(lambda):=minpoly(U,lambda);

Задание №10. Решить матричное уравнение: АХ=В, где , .

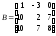> with(linalg):

> A:=matrix([[1,2,-3],[3,2,-4],[2,-1,0]]):

> B:=matrix([[1,-3,0],[10,2,7],[10,7,8]]):

> X:=linsolve(A,B);

Ответ:

Ответ:1), ;2) , ;3) , :;4) ;;,;5) ;;;;6) ;7);8) ;;;;;9) ;;;;;10) .