Обмен данными между MatLab и Excel
Запустите Excel, проверьте, что проделаны все необходимые настройки так, как описано в предыдущем разделе (MatLab должен быть закрыт). Задайте ячейкам с А1 по С3 числовой формат и введите в ячейки с A1 по C3 матрицу, для отделения десятичных знаков используйте точку в соответствии с требованиями Excel:
Выделите на листе данные ячейки и нажмите кнопку putmatrix, появляется окно Excel с предупреждением о том, что MatLab не запущен. Нажмите OK, дождитесь открытия MatLab. Появляется диалоговое окно Excel со строкой ввода, предназначенной для определения имени переменной рабочей среды MatLab, в которую следует экспортировать данные из выделенных ячеек Excel. Введите к примеру, М и закройте окно при помощи кнопки OK. Перейдите к командному окну MatLab и убедитесь, что в рабочей среде создалась переменная М, содержащая массив три на три:
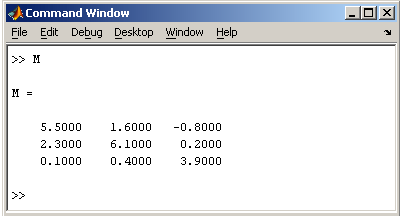
Проделайте некоторые операции в MatLab с матрицей М, например, обратите ее:
IM=inv(M)
Вызов inv для обращения матрицы, как и любой другой команды MatLab можно осуществить прямо из Excel. Нажатие на кнопку evalstring, расположенную на панели Excel Link, приводит к появлению диалогового окна, в строке ввода которого следует набрать команду MatLab: IMM=inv(M). Если теперь вернуться в MatLAB и набрать IMM <Enter>, то получим результат обращения матрицы М, совпадающий с матрицей IM. Результат аналогичен полученному при выполнении команды в среде MatLab.
Вернитесь в Excel, сделайте текущей ячейку A5 и нажмите кнопку getmatrix. Появляется диалоговое окно со строкой ввода, в которой требуется ввести имя переменной, импортируемой в Excel. В данном случае такой переменной является IM. Нажмите OK, в ячейки с A5 по A7 введены элементы обратной матрицы.
Итак, для экспорта матрицы в MatLab следует выделить подходящие ячейки листа Excel, а для импорта достаточно указать одну ячейку, которая будет являться верхним левым элементом импортируемого массива. Остальные элементы запишутся в ячейки листа согласно размерам массива, переписывая содержащиеся в них данные, поэтому следует соблюдать осторожность при импорте массивов.
Вышеописанный подход является самым простым способом обмена информацией между приложениями — исходные данные содержатся в Excel, затем экспортируются в MatLab, обрабатываются там некоторым образом и результат импортируется в Excel.
Справочные данные
Набирая в любой ячейке следующие формулы, можно получать следующие результаты:
=MLAutoStart(«no») - MatLab не будет загружаться автоматически вместе Excel;
=MLClose() – закрывает Excel Link и MATLAB;
=MLOpen()– инициирует Excel Link и MATLAB.
=MLPutMatrix("var_name"; diap) – копирует в матрицу var_name данные из диапазона diap (пример: =MLPutMatrix("s"; A1:C5));
=MLAppendMatrix("var_name"; diap) – добавляет к существующей матрице var_name диапазона diap; функция сама определяет по размерности как добавить данные (справа или снизу);
=MLGetMatrix("var_name"; "diap") – копирует матрицу в Excel, на верхний левый угол указывает диапазон diap;
Задание 2. Данные о клиентах банка представлены в файле ДаныеКлиентов.xls. Требуется передать эти данные из Excel в MatLAB и там создать программу, которая выполняет следующую обработку.
Задание для студентов с четными номерами компьютеров:
- найти номера самого молодого и самого старого клиента;
- найти номер клиента, у которого размер кредита больше среднемесячного дохода в наибольшее число раз;
- построить поле точек, отражающее зависимость размера взятого кредита от веса клиента и его среднемесячного дохода.
Номера найденных клиентов вывести в Excel, поле точек построить в MatLAB.
Задание для студентов с нечетными номерами компьютеров:
- найти номера клиентов, предоставивших неверные сведения о стаже работы или возрасте. Для этого надо сравнить стаж работы и возраст. Предполагается, что работать человек может начинать с 18 лет;
- найти, во сколько раз суммарный размер кредитов, взятых мужчинами, больше чем суммарный размер кредитов, взятый женщинами;
Номера найденных клиентов и во сколько раз отличаются суммы кредитов вывести в Excel.
Внимание! В программе не следует использовать функцию clear, так как в противном случае переданная из Ecxel информация будет стерта!
Задание 3. Получение данных из Интернет и их анализ. Подключиться к Интернет. ЗапуститьExcel2007 и создать новый документ. Перейти на вкладку «Данные» - «Из Веба» - в строке адреса ввести адрес «http://cbr.ru/currency_base/dynamics.aspx» - выбрать валюту «Доллар США» и диапазон за последние 6 месяцев – отметить пункт «таблица» - нажать «получить» - в левом верхнем углу таблицы щелкнуть желтую стрелочку, что приведет к выделению таблицы – внизу нажать кнопку «Импорт» и указать куда поместить данные. Сохраните документExcel.
В Excel2003 начинать процедуру запроса надо так: создать новый документ - «Данные» - «Импорт внешних данных» - «Создать веб-запрос». Далее аналогично.
Полученные данные передать в MatLABи в нем построить график изменения курса доллара, изобразить три первых уровня Фибоначчи и сделат заключение о целесообразности покупки или продажи валюты на сегодняшний день.
Задание 4. Решить задачу линейного программирования, представленную на карточке, выданной преподавателем. Построить многоугольник решений и поверхность целевой функции.
Пример построения многоугольника решений и поверхности целевой функции.
x = 0 : 80; % диапазон для построения
y1 = max(75 - x, 0); % x + y <= 75 ограничение на землю
y2 = max((4000 - 110 * x)/30, 0); % 110x + 30y <=4000 ограничение на хранение
y3 = max((15000 - 120 * x)/210, 0); % 120x + 210y <= 15000 затраты
ytop = min([y1; y2; y3]); % нас интересуют нижние области, т.к. оператор меньше равно
area(x, ytop); % прорисовываем области
hold on; % включение режима сохранения графика
[u v] = meshgrid(0 : 80, 0 : 80);
z=143*u+ 60 *v; %целевая функция
contour(u,v,z,20); % изображение линий уровня
holdoff; % отключение режима сохранения графика
figure% создаем новое графическое окно
surf(u,v,z) % построение трехмерной поверхностити
zlabel('ПРИБЫЛЬ'),xlabel('пшеница'),ylabel('рожь')
Пример. Для решения задачи ЛП применяется команда linprog, а именно, для следующей формулировки задачи ЛП:
минимизировать minХ (f* Х) при условии A*Х≤b, где Х – вектор переменных.
При необходимости найти максимум целевой функции, надо перед ней поставит знак минус и искать минимум этой модифицированной целевой функции, то есть:
Программный код решения:
f= [-143 -60]; % коэффициенты при целевой функции
A= [120 210; 110 30; 1 1;-1 0; 0 -1];
b = [15000; 4000; 75; 0; 0];
[Х,fval] =linprog(f,A,b); %решение задачи ЛП
X % результат решения
-f*Х % значение целевой функции
В полученное решение имеет вид:
x =
21.8750
53.1250
Значение целевой функции:
ans=
6.3156e+003
Задание 5. Количество обращений на станции технического обслуживания зависит от стоимости автомобиля. Анализу подверглось всего 28 авто разной цены. Статистические данные представлены в таблице. В клетках таблицы указано количество ситуаций, соответствующих данному числу обращений и стоимости авто. Например, двойка, выделенная красным цветом, означает, что 1 обращение на станцию ТО имело 2 машины, чья стоимость лежит в диапазоне от 100 000 до 600 000 руб.
|
|
Y - количество обращений на станции тех. обслуживания, в год | |||
|
X - диапазон стоимости автомобмля , руб. |
1 |
2 |
3 |
5 |
|
До 99 999 |
|
1 |
2 |
6 |
|
100 000 – 600 000 |
2 |
2 |
5 |
2 |
|
Свыше 600 000 |
5 |
2 |
1 |
|
Построить на графике точки, координаты которых соответствуют статистическим данным из таблицы и линию регрессии YнаX(использовать линейную регрессию). Сколько, предположительно, будет обращений на станцию для авто, стоимость которого составляет 475 000 руб.
Пример. В зависимости от размера вклада в разных банках предлагают различный процент доходности по депозитам физических лиц. Количество соответствующих вкладов указано внутри клеток таблицы 1:
Таблица1 – Распределение вкладов
|
х-размер вклада,
|
Середина интервала для х |
y- доходность вклада | ||
|
10% |
15% |
20% | ||
|
100–1000 тыс. руб. |
550 тыс. руб. |
5 |
1 |
|
|
1001-2000 тыс. руб. |
1500 тыс. руб. |
|
3 |
2 |
Текст программы на языке MatLABдля рассматриваемого примера:
clc,clear
x=[550 550 550 550 550 550 1500 1500 1500 1500 1500]'
y=[10 10 10 10 10 15 15 15 15 20 20]'
n=length(x)
yr=zeros(n,1); % вектор для хранения значений линии регрессии
b = glmfit(x,y, 'normal') % расчет коэффициентов модели. Возможна запись glmfit(x,y)
yr=b(2,1)*x+b(1,1) % рассчитываем вектор yлинейной модели регрессии
yfit = glmval(b,x,'identity') %расчет вектора yс использованием встроенной функции
plot(x,y,'*',x,yfit,'o',x,yr,'-o')
axis( [ 200, 1800, 0, 25] ) % масштаб по осям: axis([xmin,xmax,ymin,ymax])
grid on,xlabel('X'),ylabel('Y')
Получаем коэффициенты линейной модели b = 7.2632 0.0065
Замечание. Если первый (последний) интервалы переменных открыты, то следует считать ширину интервала равной второму (предпоследнему) интервалу.
Задание 6. Количество обращений на станции технического обслуживания зависит от стоимости автомобиля и его марки. Анализу подверглось всего 28 авто разной цены. Статистические данные представлены в таблице. В клетках таблицы указано количество ситуаций, соответствующих данному числу обращений и стоимости авто, а также марке автомобиля.
|
|
Y - количество обращений на станции тех. обслуживания, в год | |||
|
X - диапазон стоимости автомобмля , руб. |
1 |
2 |
3 |
5 |
|
До 99 999 |
|
1 ВАЗ |
2, из них 1 ВАЗ и 1 УАЗ |
6 из них 3 ВАЗ и 3 УАЗ |
|
100 000 – 600 000 |
2 ВАЗ |
2 УАЗ |
5 из них 2 ВАЗ, 2 УАЗ и 1 Ford |
2 из них 1 УАЗ и 1 Ford |
|
Свыше 600 000 |
5 Ford |
2 Ford |
1 Ford |
|
Построить на 3D-графике точки, координаты которых соответствуют статистическим данным из таблицы и точки регрессииYнаX(использовать линейную регрессию). Сколько, предположительно, будет обращений на станцию для автоFord, стоимость которого составляет 475 000 руб.
Пример. Рассмотрим предыдущий пример, добавивк переменной х1 – «размер вклада» еще одну переменную х2 – «возраст вкладчика». Пусть таблицаисходных имеет вид:
Таблица 2 – Распределение вкладов с учетом возраста
|
х-размер вклада, тыс. руб. |
Середина интервала для х |
y- доходность вклада, % | ||
|
10 |
15 |
20 | ||
|
100 - 1000 |
550 |
5 из них 2 вклада от лиц возрастом в диапазоне 20-30лет и три в диапазоне 30-40лет |
1 возраст вкладчика в диапазоне 20-30лет |
|
|
1001 -2000 |
1500 |
|
3 из них 1 вклад от лица возрастом в диапазоне 30-40лет и два в диапазоне свыше 40лет |
2 из них 1 вклад от лица возрастом в диапазоне 20-30лет и один в диапазоне свыше 40лет |
Текст программы на языке MatLABдля рассматриваемого примера:
%Программа расчитывает коэфф-ты регрессионной модели y=b1+b2x1+b3x2
%где х1- размер вклада, х2 - возраст вкладчика
clc,clear
x1=[550 550 550 550 550 550 1500 1500 1500 1500 1500]'
x2=[25 25 35 35 35 25 35 45 45 25 45]' %берем середины диапазонов возрастов
y=[10 10 10 10 10 15 15 15 15 20 20]'
n=length(x1)
yr=zeros(n,1); % вектор для хранения значений линии регрессии
X=[x1 x2] % сформировали объединенный вектор
yr=zeros(n,1); % вектор для линии регрессии
distr='normal'; % предполагаемое распределение y
b = glmfit(X,y,distr) % расчет коэффициентов модели.
yr=b(3,1)*X(:,2)+b(2,1)*X(:,1)+b(1,1) % расчет вектора y
yfit = glmval(b,X,'identity') % расчет вектора yс использованием встроенной функции
plot3(X(:,1),X(:,2),y,'*') % точки исходных данных
pause
holdon% включили режим сохр. графиков, чтобы три 3Dграфика были в одном окне
plot3(X(:,1),X(:,2),yr,'ro') % точки yr
plot3(x1,x2,yfit,'g+') % точки yfit
xlabel('X1'),ylabel('X2'),zlabel('Y')