Основы криптологии

Мейн - Рыков Александр Алексеевич

Саб - Яшин Илья Александрович

Математические основы криптологии

Б. Шнайер – прикладная криптография

Харин, Берник и т.д. – основы криптологии

Х.К.А. ван Тилборг – основы криптологии

1. Множества и отображения

Множество – определенная совокупность объектов.

Объекты, из которых состоит множество, называются его элементами.

Множество обозначается большой прописной буквой алфавита, а его элементы – строчными буквами алфавита.

Множества с конечным числом различных элементов могут быть описаны путем явного перечисления всех элементов. Обычно эти элементы заключаются в фигурные скобки.

S={a₁,a₁,...,a_k}

Множество S, состоящее из конечного числа элементов, называется конечным множеством, а само это число называется порядком множества S - #S.

Для некоторых особо важных множеств приняты стандартные обозначения, которых следует придерживаться:

N – множество натуральных чисел;

Z – множество целых чисел;

P – множество простых чисел;

Q – множество рациональных чисел;

R – множество вещественных чисел.

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

1. Перечисление элементов;

2. Характеристическим предикатом – S={x|P(x)};

3. Порождающей процедурой – {x|x:=f}.

Характеристический предикат – некоторое условие, выраженное в форме логического утверждения или процедуры. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит.

Перечислением можно задать только конечное множество. Бесконечное множество задается характеристическим предикатом или порождающей функцией.

При заданном множестве S включение a S указывает на то, что а – элемент множества. В противном случае а S.

Говорят, что S – подмножество Т или S c Т(S содержится в Т), когда имеет место импликация:

X 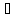S, Ax=>x 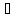T

Два множества совпадают(или равны), если у них одни и те же элементы. Символически:

S=T  ScT, TcS

Пустое множество – зачеркнутый круг – множество, не содержащее ни одного жлемента. По определению – вхзодит в число подмножеств любого множества.

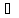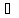Пересечение множеств: S T={x|xS, xT}

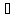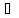Объединение множеств: S u T={x|xS или xT}

Пусть X и Y – произвольные множества.

Пару (x,y) x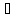X,y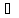Y взятых в данном порядке, называют упорядоченной парой, считая при этом, что (x1,y1)=(x2,y2) тогда и только тогда, когда x1=x2, y1=y2.

Декартовым произведением двух множеств Х и Y называется множество всех упорядоченным пар (х,у)

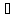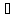X*Y={(x,y)|xX,yY}

Пусть, R – множество всех вещественных чисел.

Тогда декартов квадрат R^2=R*R есть просто множество всех декартовых координат на плоскости относительно заданных координатных осей.

Аналогично можно ввести декартово произведение трех четырех и т.д. множеств.

Отображения

Понятие отображения или функции является одним из центральных в математике.

При заданных Х и Y отображение f с областью определения Х и областью значений Y сопоставляет каждому элементу х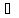Х элемент f(x)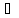Y

Символическои отображение записывается в виде f:X->Y.

Образом при отображении f называется множество всех элементов вида f(x):

Im f = {f(x)|x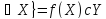

Множество f^-1(y) = {x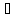X|f(x)=y} называется прообьразом элемента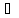 yY.

Im – прообраз.

Отображение f:X->Y называется сюрьективным, когда Im f=Y.

Отображение f:X->Y называется сюрьективным(или сюрьекцией, отображением на У), если каждый элемент множества Y является образом хотя бы одного элемента множества Х, то есть:

//картинко

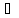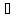уY ExX y=f(x)

Отображение f:X->Y называется инъекцией(или вложением в множество Y), если разные элементы множества Х переводятся в разные элементы множества У.

Формально, это значит, что если два образа совпадают, то совпадают и прообразы. F(x)=f(y)=>x=y.

Инъективность является необходимым условием биективности(достаточно вместе с сюръективностью).

Функция f:X->Y называется биецией(f:X<->Y) если она:

Переводит разные элементы множества Х в разные элементы множества Y(инъективность).

2 - ?

В двух множествах элементы совпадают по индексам.

Множества, для которых существует биекция, называются равномощными.

Равенство f=g двух отображений означает по определению, что их соответствующие области совпадают.

Единичным или тождественным отображением e_x:X->X называется отображение, переводящее каждый элемент x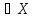 в себя.

Отображение f^-1 является обратным к f, если f(x)=y  f^-1(y)=x

Бинарные отношения

Для любых двух множеств Х и Y всякое подмножество ОсХ*Y называется бинарным отношением между Х и Y.

Бинарное отношение ~ на X называется отношением эквивалентности, если для всех х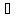X выполнены условия:

1. x~x(рефлективность)

2. x~x1=>x1~x(симмметричность)

3. x~x1, x1~x2=>x2~x (транзитивность)

Подмножество Н={x’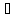X|x’~x} HcX всех элементов, эквивалентных данному х, называется классом эквивалентности, содержащим х.

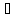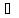Так как x~x (условие 1), то x’H. Любой элемент x’H называется представителем класса Н.

Справедлива следующая теорема:

Теорема 1: множество классов эквивалентности по отношению ~ является разбиением множества Х в том смысле, что Х является объединением непересекающихся подмножеств.

//-----------------------------

//-1 лекция

//-----------------------------