Общая физика. Оптика / Шпоргалки / 10-11 н

10. Электроемкость. Конденсаторы

Электроемкостью уединенного проводника называется физическая величина, равная отношению заряда проводника к его потенциалу в поле этого заряда:

. (3.5)

Электроемкость проводника показывает, какой заряд необходимо сообщить проводнику для того, чтобы его потенциал принял заданное значение. Чем больше заряд проводника, тем больше его потенциал в поле этого заряда. Поэтому электроемкость не зависит ни от величины заряда проводника, ни от значения его потенциала, а зависит только от размера и формы проводника, а также от диэлектрических свойств среды, в которой он находится. Единица измерения электроемкости проводника в СИ называется фарад (обозначается 1 Ф): .

Рассмотрим определение емкости проводящего шара радиусом R, находящегося в вакууме. Для этого сообщим шару произвольный заряд Q. Заряд равномерно распределится по поверхности шара с поверхностной плотностью , которая будет одинакова в каждой точке поверхности шара. Этот заряд создаст электростатическое поле, напряженность которого определяется следующим образом (см. пример 1, п. 1.7):

Вид функции – гипербола (), а коэффициент пропорциональности зависит только от заряда шара. Потенциал шара можно будет найти так:

.

В соответствии с (3.5) емкость шара

. (3.6)

Электроемкостью конденсатора называется физическая величина, равная отношению заряда конденсатора к разности потенциалов, создаваемой полем этого заряда между его обкладками:

. (3.7)

Так же, как и емкость проводника, электроемкость конденсатора не зависит ни от величины заряда конденсатора, ни от разности потенциалов между его обкладками, а зависит только от размера и формы конденсатора, а также от диэлектрических свойств среды между обкладками конденсатора. Следует отметить, что электроемкость конденсатора не зависит от наличия вблизи него других проводящих или диэлектрических тел.

В качестве примера выведем формулу емкости плоского конденсатора, изображенного на рис. 3.9, а. Определим напряженность электростатического поля, создаваемого одной заряженной пластиной площадью S. Силовые линии такого поля изображены на рис. 3.10. Если рассмотреть точки пространства, расположенные настолько близко к пластине, что расстояние от них до пластины существенно меньше, чем до ее границ (из этих точек пластина будет представляться как бесконечно большая плоскость), то искривлением силовых линий у границ пластины можно пренебречь (рис. 3.11). Таким образом, бесконечно большая заряженная плоскость создает однородное поле. Исходя из симметричности системы, модуль напряженности поля во всех точках, равноудаленных от пластины, должен быть одинаковым, а направление вектора зависит только от положения исследуемой точки пространства (слева или справа от пластины).

Определим напряженность поля в некоторой точке с координатой x, отсчитываемой вдоль оси , направленной перпендикулярно пластине. Для этого в качестве гауссовой поверхности выберем поверхность цилиндра, ось которого перпендикулярна плоскости, а основание имеет площадь (рис. 3.12). Модуль напряженности поля одинаков во всех точках оснований цилиндра, исходя из симметрии системы. Угол между и внешней нормалью к поверхности во всех точках боковой поверхности цилиндра равен , а во всех точках левого и правого оснований гауссова цилиндра равен 0.

Определим поток напряженности поля через выбранную поверхность.

,

где – площадь левого основания гауссова цилиндра; – площадь правого основания гауссова цилиндра; – площадь боковой поверхности гауссова цилиндра. Получаем

; ;.

Таким образом,

. (3.8)

Определим алгебраическую сумму зарядов, охваченных поверхностью гауссова цилиндра. В данном случае электрический заряд, попавший внутрь него – это заряд “вырезанной” цилиндром части пластины. Его можно найти, умножив площадь основания цилиндра на поверхностную плотность заряда пластины:

. (3.9)

Приравняем (3.8) и (3.9) с учетом коэффициента :

. (3.10)

Полученное соотношение определяет модуль напряженности однородного поля бесконечно большой заряженной пластины.

Если две разноименно заряженные пластины расположить на малом расстоянии друг от друга так, чтобы выполнялось условие однородности поля каждой из них (рис. 3.13), то напряженность поля можно будет определить по принципу суперпозиции с учетом (3.10):

В этом случае разность потенциалов между обкладками получившегося конденсатора можно определить так:

.

Емкость плоского конденсатора, по определению (3.7), составит

.

Следует учесть, что если пространство между обкладками любого конденсатора заполнить диэлектриком с относительной диэлектрической проницаемостью , то при том же значении заряда обкладок напряженность поля между обкладками уменьшится в  раз. Поэтому в  раз уменьшится разность потенциалов между ними, а, следовательно, в  раз увеличится емкость конденсатора:

.

Тогда

. (3.11)

Выведем формулу емкости сферического конденсатора. Рассмотрим систему сферических обкладок, изображенную на рис. 3.9, в. Поместим на внутреннюю обкладку заряд Q, а на внешнюю заряд . Напряженность электростатического поля, созданного такой системой зарядов можно описать следующей формулой:

Определим разность потенциалов между обкладками, пользуясь дифференциальной связью напряженности и потенциала (1.13):

.

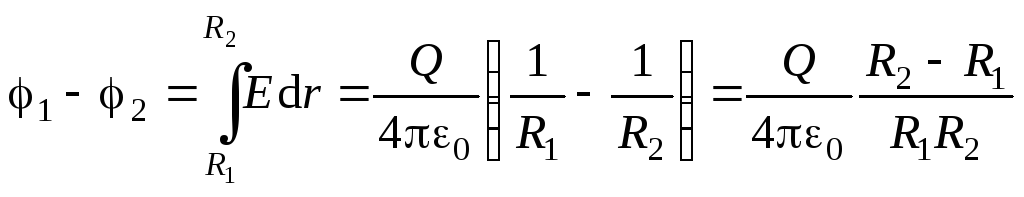Емкость сферического конденсатора, по определению (3.7), составит

.

Если конденсатор заполнен диэлектриком с относительной диэлектрической проницаемостью , то

. (3.12)

Подчеркнем еще раз, что емкость конденсатора зависит от размера, формы конденсатора и относительной диэлектрической проницаемости диэлектрика между его обкладками.

11. Энергия электрического поля.

Объемная плотность энергии

Рассмотрим процесс зарядки уединенного проводника. Чтобы его заряд достиг величины Q, будем сообщать проводнику заряд порциями dq, перенося их из бесконечно удаленной точки 1 на поверхность проводника в точку 2 (рис. 3.14). Для передачи проводнику новой порции заряда внешние силы должны совершить работу против сил электрического поля: . Поскольку проводник уединенный (точка 1 бесконечно далека от проводника), то . Потенциал точки 2 равен потенциалу проводника . Поэтому . Если проводнику передан заряд q, то его потенциал . Полная работа внешних сил по зарядке проводника до значения заряда Q будет равна

.

Согласно закону сохранения энергии, работа внешних сил по зарядке проводника увеличивает энергию создаваемого электростатического поля, т.е. проводник запасает определенную энергию:

. (3.13)

Рассмотрим процесс зарядки конденсатора от источника ЭДС. Источник в процессе зарядки переносит заряды с одной пластины на другую, причем сторонние силы источника совершают работу по увеличению энергии конденсатора:

,

где Q – заряд конденсатора после зарядки. Тогда энергия электрического поля, созданного конденсатором, определится как

. (3.14)

Выражение (3.14) позволяет записать величину энергии электростатического поля двумя способами:

и .

Сопоставление двух соотношений позволяет задать вопрос: что является носителем электрической энергии? Заряды (первая формула) или поле (вторая формула)? Оба записанных равенства прекрасно согласуются с результатами экспериментов, т.е. расчет энергии поля можно одинаково правильно вести по обеим формулам. Однако такое наблюдается только в электростатике, т.е. когда осуществляется расчет энергии поля неподвижных зарядов. При рассмотрении теории электромагнитного поля в дальнейшем (гл. 8) мы увидим, что электрическое поле может создаваться не только неподвижными зарядами. Электростатическое поле – это частный случай электромагнитного поля, существующего в пространстве в виде электромагнитной волны. Его энергия распределена в пространстве с определенной плотностью. Введем понятие объемной плотности энергии поля следующим образом.

Преобразуем последнее равенство (3.14) для случая плоского конденсатора, воспользовавшись связью разности потенциалов и напряженности однородного поля:

,

где – объем конденсатора, т.е. объем части пространства, в котором создано электрическое поле.

Объемной плотностью энергии поля называется отношение энергии поля, заключенного в малом объеме пространства к этому объему:

. (3.15)

Следовательно, энергию однородного электрического поля можно рассчитать так: .

Сделанный вывод можно распространить на случай неоднородного поля таким образом:

, (3.16)

где – такой элементарный объем пространства, в пределах которого поле можно считать однородным.

Для примера рассчитаем энергию электрического поля, созданного уединенным металлическим шаром радиусом R, заряженным зарядом Q, и находящимся в среде с относительной диэлектрической проницаемостью . Повторив рассуждения примера из п.2.5, получим модуль напряженности поля в виде функции :

Тогда выражение для объемной плотности энергии поля примет вид:

Поскольку напряженность поля зависит только от радиальной координаты, то она будет практически постоянна в пределах тонкого сферического слоя с внутренним радиусом r и толщиной (рис. 3.15). Объем этого слоя . Тогда энергия поля определится так:

.

Аналогичный результат мы бы получили, если бы вычисляли энергию заряженного шара по формуле (3.13), воспользовавшись (3.6):

.

Однако следует помнить, что такой способ неприменим, если необходимо найти энергию электрического поля, заключенную не во всем объеме поля, а лишь в его части. Также метод расчета по формуле (3.13) нельзя использовать при определении энергии поля системы, для которой неприменимо понятие “емкость”.