32. Затухающие колебания в последовательном колебательном контуре

В предыдущем параграфе мы рассмотрели процесс свободных (незатухающих) гармонических колебаний в контуре при отсутствии активного сопротивления. Проанализируем теперь колебательный процесс, происходящий в контуре при наличии сопротивления (рис. 9.4). При разрядке конденсатора в контуре возникнут колебания тока и заряда. Причина перезарядки конденсатора та же – появление ЭДС самоиндукции. Однако теперь при наличии тока в цепи будет происходить необратимое выделение количества теплоты на активном сопротивлении, что приведет к уменьшению максимального заряда конденсатора по истечении периода колебаний. Выведем уравнение колебаний в этом случае.

Примем направление тока зарядки конденсатора за положительное. Поскольку заряжается конденсатор за счет работы самоиндукции, то полярность ЭДС самоиндукции в процессе зарядки конденсатора будет такой, как указано на рис. 9.4 (положительное направление тока в цепи от “+” к “–” источника). Так как конденсатор при этом заряжается, то полярность заряда обкладок тоже будет такой, как на рисунке (ток, т.е. движение положительных зарядов, направлен в сторон положительно заряжающейся обкладки). Запишем для участка цепи 2–L–1 обобщенный закон Ома:,

где ,. После подстановки и преобразований получаем:(9.9)

Если обозначить,, то уравнение (9.9) приводится к видудифференциального уравнения затухающих колебаний .

Как было показано в п.5.5 первой части курса, решением такого уравнения является функция вида

, (9.10)

где  – частота затухающих колебаний. Если подставить это решение в (9.9), то можно определить, что (9.11)

Поскольку амплитуда колебаний уменьшается с течением времени, то, строго говоря, затухающие колебания нельзя называть гармоническими. Тем не менее для них тоже вводится понятие периода (условного периода) колебаний:

.

Рассмотрим характеристики затухающих колебаний. Первая из них, непосредственно входящая в закон изменения колеблющейся величины, это коэффициент затухания . Если выразить отношение амплитуд колебаний в моменты времени и, то можно получить

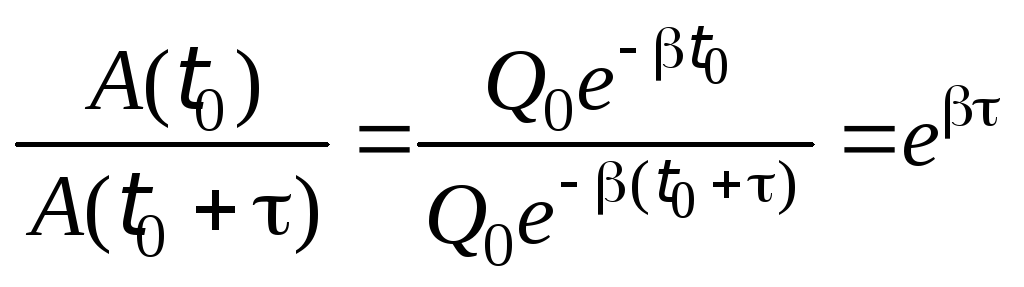. (9.12)

Если за время  амплитуда колебаний уменьшилась в е раз, то , поэтому. Таким образом, коэффициент затухания, обратно пропорционален времени, за которое амплитуда колебаний уменьшается в е раз.

Также для количественной характеристики быстроты убывания амплитуды затухающих колебаний вводится понятие логарифмического декремента :(9.13)

Если за время NT система совершит N колебаний, и их амплитуда уменьшится в е раз, то . Таким образом,логариф-мический декремент – безразмерная величина, обратная числу колебаний N, в течение которых амплитуда колебаний уменьшается в e раз.

Также затухающие колебания характеризуются величиной добротности контура. Ввести понятие добротности можно несколькими способами. Сейчас сделаем это так:. Чтобы выяснить смысл добротности, рассмотрим энергию электрического поля контура:

.

Первоначальный запас энергии в контуре – это максимальное значение , т.е.

.

Тогда скорость убывания энергии контура определится как

.Следовательно, за один период энергия контура уменьшится на величину

.

Отношение убыли энергии контура за период к первоначальному ее запасу составляет(9.14)

Таким образом, добротность колебательного контура пропорциональна отношению энергии, запасенной в контуре, к ее убыли за один период.

Проанализируем решение уравнения затухающих колебаний. Из (9.11) видно, что что при колебания в системе не возникают. В этом случае наблюдаетсяапериодический процесс (рис. 9.5), в результате которого вся запасенная в контуре энергия расходуется на выделение тепла в резисторе. Каким из двух способов, показанных на рис. 9.5, система вернется в положение равновесия, зависит от начальных условий.

Если же колебания возникли, то нетрудно увидеть, что их период будет больше периода незатухающих колебаний:

.

Если колебания заряда конденсатора осуществляются по закону (9.10), то колебания напряжения на обкладках конденсатора подчиняются зависимости

,

т.е. происходят синхронно с колебаниями заряда.

Закон колебаний силы тока в контуре найдем так: (9.15)

. Т.к. из (9.11) следует, что , то умножим (9.15) на(равенство от этого не нарушится):

.Если обозначить ,, то.

Полученное соотношение показывает, что колебания тока опережают колебания заряда по фазе на . Причем, т.к., а, то.

Ранее мы обнаружили, что при незатухающих колебаниях разность фаз колебаний тока и заряда составляла . Теперь мы видим, что при наличии затухания в контуре сдвиг фаз увеличивается.

Если затухание в контуре невелико, т.е. , то. В этом случае логарифмический декремент будет равен

.

Добротность контура

, (9.16) т.е. она равна отношению волнового сопротивления контура к его активному сопротивлению. Из (9.11) следует, что колебания в контуре возникают при , т.е. при. Поэтому сопротивление контура должно удовлетворять неравенству:. Сравнивая это выражение с (9.16), получим, что в таком случае добротность контура.