25. Токи при размыкании и замыкании цепей, содержащих индуктивность

Найдем законы изменения силы тока в цепи при ее замыкании или размыкании, т.е. при неустановившемся режиме в цепи. Допустим, что источник с ЭДС E замыкается в цепь, содержащую резистор сопротивлением R и катушку индуктивностью L (рис. 6.13). Поскольку сила тока в цепи будет возрастать, то в катушке возникнет явление самоиндукции, в результате чего в процессе изменения тока в цепи будут существовать сразу две ЭДС – исходного источника и ЭДС самоиндукции. Запишем выражение закона Ома в этом случае:

.

Подставим (6.10) в эту формулу и приведем ее к виду

.

Полученное дифференциальное уравнение решим, разделив переменные:

, .

Проинтегрировав последнее выражение, получим

,

где постоянная интегрирования С должна быть найдена из начальных условий процесса. В окончательном виде закон изменения силы тока в цепи будет выглядеть так:

. (6.13)

Рассмотрим применение этого уравнения для решения задачи в двух случаях.

Пример 1. Замыкание цепи. В этом случае начальные условия будут выглядеть так: ;. Подставим их в (6.13):

,

откуда . Тогда закон (6.13) принимает вид:

. (6.14)

Из этого выражения видно, что значение силы тока в цепи установится равным при. Это означает, что теоретически самоиндукция постоянно будет существовать при нарастании тока в цепи, а, согласно правилу Ленца, сущность самоиндукции – противодействие нарастанию силы тока. График, иллюстрирующий соотношение (6.14) при различных индуктивностях цепи (), представлен на рис. 6.14.

П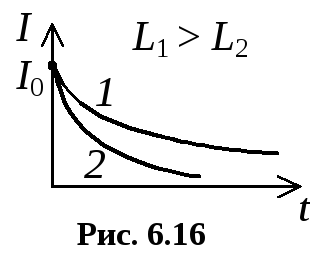ример 1. Размыкание цепи. Пусть в цепи на рис. 6.15 источник тока отключается от катушки, которая замыкается на резистор. Начальные условия для решения уравнения в этом случае будут выглядеть следующим образом: ;;. Подставим их в (6.13):

,

откуда . Закон (6.13) принимает вид:

. (6.15)

Теоретически это означает, что сила тока в цепи постоянно будет отлична от нуля, хотя и будет стремиться к этому значению с течением времени (рис. 6.16).

Анализ графиков приводит нас к следующему выводу: при размыкании и замыкании цепей, содержащих индуктивность, процесс установления силы тока в цепи продолжается тем дольше, чем больше величина индуктивности.