Численные методы (Шапошникова Д.А.) / Занятия / Занятия 8-9 ИЭТ Аппроксимация

Методы вычислений. ИЭТ. 4-й семестр. Занятие 8. Стр. 5

ЗАНЯТИЕ 8

Приближение функций

интерполяция, многочлены Чебышева

Вопросы к занятию

1. Аппроксимация — что это такое? Сформулировать постановку задачи аппроксимации функции.

2. Постановка задачи интерполяции.

3. Обобщенный многочлен — что это?

4. Интерполяционный многочлен.

5. Интерполяционный многочлен Лагранжа.

6. Пример Рунге.

7. Постановка задачи о многочленах наилучшего равномерного приближения.

8. Многочлены Чебышева. Определение. Свойства.

9. Интерполяционный многочлен, построенный на «чебышевских» узлах.

Справочные сведения

Задача интерполяции: по заданной таблице чисел найти такую функцию , что , и для . Точки называют узлами интерполяции, а функцию — интерполирующей функцией; если — многочлен, то ее называют интерполяционным многочленом.

Классическое решение задачи интерполяции — построение обобщенного интерполяционного многочлена , где — заданные базисные функции, а —коэффициенты обобщенного многочлена. При , то получаем интерполяционный многочлен Лагранжа: .

Задача о наилучшем равномерном приближении. Минимизация оценки погрешности интерполяции. Найти такие узлы интерполяции, чтобы погрешность интерполяции была минимальной. Минимум погрешности интерполяции на отрезке достигается в нулях многочлена Чебышева.

Многочлены Чебышева. , при , .

Многочлен Чебышева — алгебраический многочлен n-й степени.

, , , , , …

1. Легко видеть, что многочлены Чебышева четных степеней — четные функции, нечетных степеней — нечетные, что коэффициент при при равен .

2. Доказано, что для имеет место формула , т.е. .

Многочлен Чебышева.

3. Корни многочлена Чебышева n-й степени легко вычислить: .

4. Корни многочленов Чебышева разных степеней не совпадают.

5. Если узлы интерполяции — корни полинома Чебышева (n+1)-й степени, то погрешность интерполяции соответствующего интерполяционного многочлена n-й степени минимальна.

6. Среди всех алгебраических многочленов n-й степени с единичным коэффициентом при старшей степени многочлен менее всего отклоняется от нуля: ; многочлены Чебышева часто называют многочленами наименее уклоняющиеся от нуля.

Например, погрешность интерполяции функции Рунге многочленом Лагранжа с чебышевскими узлами стремится к нулю с ростом степени интерполяционного многочлена.

Задача 1. Построение интерполяционного полинома Лагранжа. Запишем многочлены Лагранжа первой и второй степени для функции для случаев а) ; б) .

Заметим, что рассматриваемый пример — искусственный. Задача интерполяции редко возникает для функций, заданных аналитически, и то, только тогда, когда вычисление функции требует очень большого числа арифметических операций. Однако свойства интерполяционного многочлена хорошо видны, когда он записывается для хорошо известной функции.

Прежде чем приступать к решению задачи, запишем выражение для интерполяционного многочлена в более наглядной форме , т.е. , .

Запишем интерполяционные многочлены первой степени для узлов интерполяции и ,

, т.е. практически совпадает с многочленом Тейлора первой степени в окрестности нуля;

;

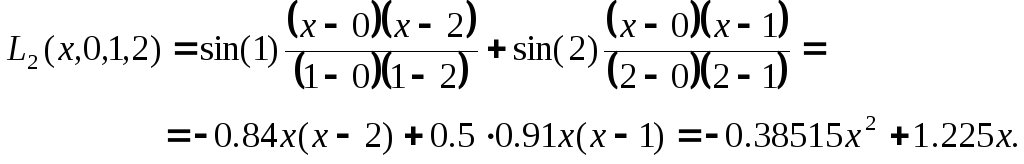
Задача 2. Исследование свойств интерполяционного полинома Лагранжа. Обсуждение домашнего задания. Построим интерполяционный многочлен Лагранжа для функции Рунге по равномерной сетке на отрезке . Для этого определим значение N > 4, построим равномерную сетку из N+1 узла, опишем выражение для полинома Лагранжа как функцию переменной x и степени многочлена N, построим на одном графике график функции Рунге и многочлена Лагранжа степени N. Найдем по графику значение равномерной нормы . Изменяя значения N и наблюдая соответствующие графики можно попытаться описать свойства аппроксимации функции Рунге полиномами Лагранжа. Например, что произойдет, если вместо отрезка рассмотреть интерполяцию на промежутке ?

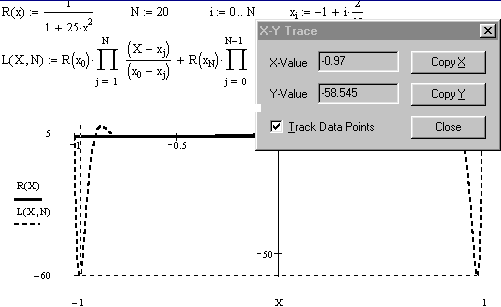
См. файл Интерполяция для Рунге равномерная сетка, записанный в папке \Методы вычислений 2006\Рабочие документы Mathcad МВ 2006.

Задача 3. Исследование свойств многочлена наилучшего равномерного приближения. Обсуждение домашнего задания.Построим для функции Рунге интерполяционный полином Лагранжа, построенный по «чебышевским» узлам интерполяции. Нагляднее всего свойства узлов интерполяции, которые являются корнями многочленов Чебышева можно продемонстрировать, вычислив по этим узлам интерполяционные многочлены Лагранжа. Для того чтобы выполнить соответствующие вычисления проще всего воспользоваться решением предыдущей задачи. Нужно добавить к ней вычисление нулей многочленов Чебышева и вычисление нового интерполяционного многочлена Лагранжа.

См. файл Интерполяция для Рунге Чебышевская сетка

Домашнее задание

Задание 13.8 Исследовать свойства аппроксимации функции Рунге интерполяционными многочленами Лагранжа, построенными по равноотстоящим узлам и по узлам, расположенным в нулях многочленов Чебышева, на отрезке . Обосновать и объяснить вычисления. Сформулировать выводы .Оформить отчет. См. файлы Интерполяция для Рунге равномерная сетка и Интерполяция для Рунге Чебышевская сетка.

Задание 14.8 Построить графики многочленов Чебышева до 10-го порядка. Вычислить и изобразить нули этих многочленов. Изобразить уклонения многочленов Чебышева от нуля. Убедиться в справедливости описанных в теории свойств многочленов Чебышева. Обосновать и объяснить вычисления. Сформулировать выводы. Оформить отчет. В Mathcad многочлен Чебышева n-й степени вычисляет функция Tcheb(n,x).