Численные методы (Шапошникова Д.А.) / Занятия / Занятие 5 ИЭТ Решение нелинейных систем

Методы вычислений. ИЭТ. 4-й семестр. Занятие 4. Стр. 4

ЗАНЯТИЕ 4

ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Вопросы к занятию

1. Постановка задачи о приближенном решении нелинейной системы .

2. Матрица Якоби. Определение.

3. Метод простых итераций решения нелинейной системы .

4. .Метод Ньютона решения нелинейной системы .

Справочные сведения

Методы решения систем нелинейных уравнений. Рассмотрим систему нелинейных уравнений c m неизвестными (записаны явно и в векторной форме):

или , где , .

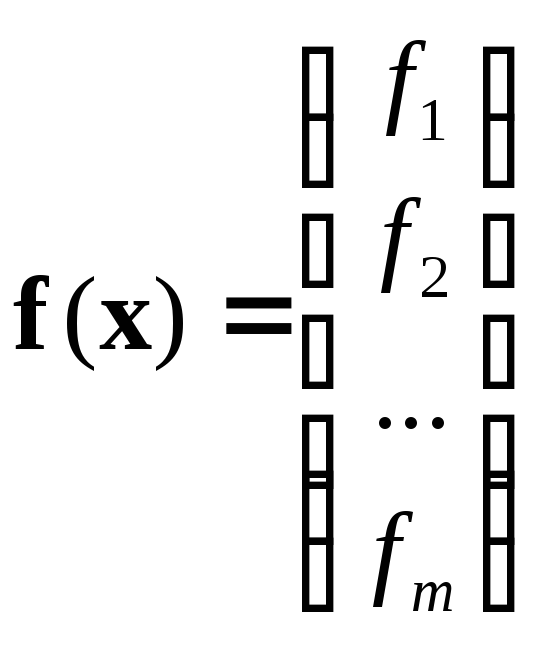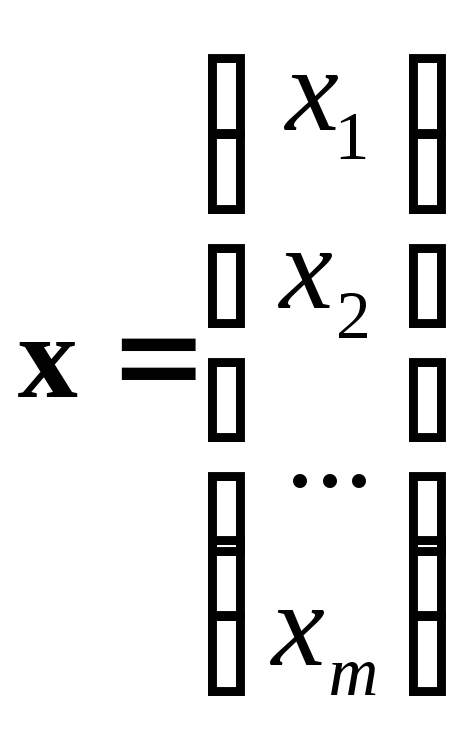Задача решения такой системы существенно сложнее задачи отыскания решения нелинейного уравнения. Прежде всего, обычно сложно установить имеет ли система решение и сколько у нее решений.

Подавляющее большинство методов решения нелинейной системы являются итерационными, они состоят в построении последовательности , сходящейся к точному решению системы , Например, при и , если .

Матрицей Якоби рассмотренной системы называют матрицу, обозначаемую или , которая определена равенством

.

Наиболее популярными методами решения нелинейной системы являются метод простых итераций и метод Ньютона.

Метод простых итераций состоит в замене исходной системы эквивалентной ей системой и построении последовательности , сходящейся при к точному решению исходной системы.

Нетрудно показать, что , где — точка принадлежащая общей окрестности точек и . Т.е. сходимость метода зависит от свойств матрицы Якоби вектор-функции . Обычно рассматривают матрицу. Поэтому достаточным условием сходимости метода является условие , например, .

На практике вычисления заканчивают, когда , где — заданная погрешность вычислений. Тогда полагают . Следует, однако, помнить, что при медленной сходимости итерационный процесс может завершиться задолго до достижения корня. С другими критериями окончания итерационного процесса можно ознакомиться отдельно. Здесь они не рассматриваются, поскольку метод простых итераций имеет смысл использовать тогда, когда итерационная последовательность сходится быстро и удовлетворительная погрешность достигается за 2-3 итерации. Порядок вычислений такой же, как и при решении уравнений.

Метод Ньютона. Пусть в окрестности решения системы (матрица Якоби обратима) и выбрано некоторое нулевое приближение . Последовательные приближения решения в методе Ньютона вычисляются по формуле , n = 0, 1, …, где — матрица, обратная к матрице Якоби. Достаточно часто пользуются упрощенным методом Ньютона, в котором — матрица Якоби и обратная к ней матрица вычисляется один раз, в точке начального приближения . Если , то в достаточно малой окрестности решения итерационный процесс Ньютона сходится, причем с квадратичной скоростью, т.е. если , то , где — точное решение системы. Вычисления заканчиваются, когда . Порядок вычислений такой же, как и при решении уравнений.

Задача 1. Решение нелинейных систем методом простых итераций. Найти с погрешностью, не превышающей , методом простых итераций решение нелинейной системы (перед началом вычислений преобразуем систему к виду, удобному для итераций)

Решение задачи 1. Зададим нулевое приближение и обозначим: , , , .

Проверим достаточное условие сходимости; итерации сходятся там, где выполнено неравенство :

, .

Достаточное условие сходимости выполнено: .

Вычислим первое приближение:

,

Видно, что требуемая точность достигнута уже на первом шаге. Таким образом, — приближенное решение, вычисленное с погрешностью, не превышающей 0.1.

Задача 2. Решение нелинейных систем методом Ньютона. Найти с погрешностью, не превышающей , методом Ньютона решение нелинейной системы

Решение задачи 2. Зададим нулевое приближение и обозначим: , , , , .

Проверим достаточное условие сходимости:

, . Достаточное условие сходимости выполнено, поскольку матрица Якоби обратима в некоторой окрестности нулевого приближения.

Вычислим первое приближение: , ,

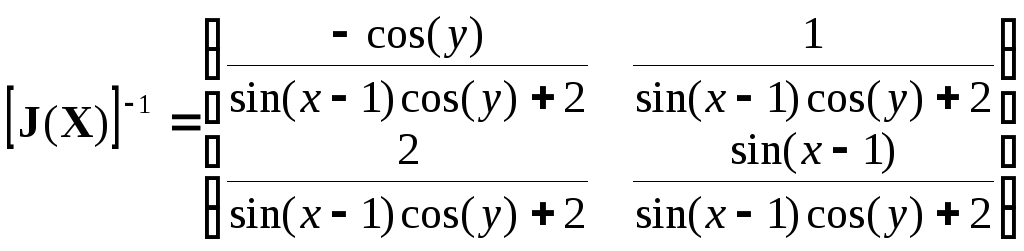Видно, что требуемая точность достигнута уже на первом шаге. Таким образом, — приближенное решение, вычисленное с погрешностью, не превышающей 0.1.

Домашнее задание

Задание 6.4 Найти методом простых итераций с погрешностью, не превышающей , решение системы . Представить отчет, содержащий результаты вычисления с подробными пояснениями и обоснованием вычислений. См. файл Нелинейные системы Простые итерации

Задание 7.4 Найти методом Ньютона с погрешностью, не превышающей , решение системы . Представить отчет, содержащий результаты вычисления с подробными пояснениями и обоснованием вычислений. См. файл Нелинейные системы МетодНьютон