Методы вычислений. ИЭТ. 4-й семестр. Лекция 3-4. Стр. 11

МЕТОДЫ ВЫЧИСЛЕНИЙ

ИЭТ, 4-й семестр, 2²

Лекция 3-4

Методы решения нелинейных уравнений

Методы решения нелинейных уравнений: постановка задач, обусловленность задач, локализация корней, характеристика итерационных методов. Методы бисекций, простых итераций, Ньютона. Методы решения систем нелинейных уравнений (метод простых итераций, метод Ньютона).

Задача численного решения нелинейных уравнений, особенно с учетом простоты рассматриваемых в курсе классов функций, может показаться несколько архаичной, учитывая возможности современных компьютеров и современного математического обеспечения. На самом деле это не так. Дело в том, что численное решение нелинейного уравнения f(x) = 0 — одна из немногих задач, которые могут быть достаточно полно исследованы в рамках нашего курса. Задача имеет простую геометрическую интерпретацию, благодаря которой становятся понятными многие сложные проблемы, возникающие при решении широкого круга вычислительных задач.

Вспомним классику. Рассмотрим уравнение f(x) = 0. Корнем (решением) уравнения называется значение , для которого справедливо .

Будем в дальнейшем полагать, что в окрестности искомого решения функция достаточно гладкая — непрерывно дифференцируема нужное число раз.

ОПР.Корень называется простым, если , но .

ОПР.Корень называется кратным, а число k — кратностью корня, если , , но .

X

- простые корни, - кратные.

Задача отыскания простых корней проще, чаще встречается, большинство численных методов предназначено для отыскания простых корней.

Из классического анализа известно:

Теорема 3.1.Если f(x) непрерывна на [a,b], и принимает на его концах значения разных знаков (f(a) f(b)<0), то на [a,b] есть хотя бы один корень уравнения f(x) = 0.

Если отрезок [a,b] содержит единственный корень уравнения, то он называется отрезком локализации.

Не существует универсальных методов определения отрезка локализации. На практике используются графики, таблицы значений функции с достаточно малым шагом, анализ поведения производной, физические соображения (анализ модели) и т.п. В рамках нашего курса будут рассмотрены задачи, в которых функция задана аналитически и существует простой корень, который можно локализовать графически.

На практике чаще всего представляют интерес не все корни уравнения, а некоторые из них (наименьший, наибольший, принадлежащий некоторому промежутку и т.п.). Найти корень аналитически (точно) — записать формулу для вычисления, в большинстве практических задач не удается, да и не очень нужно, т.к. само уравнение в большинстве практических задач не является "точной" моделью процесса, входящие в функцию параметры определяются экспериментально. Следует заметить, что зачастую сама функция не может быть представлена аналитически, а ее значения получаются как результат работы некоего алгоритма (программы).

Постановка задачи. Найти с погрешностью, не превышающей , приближенное значение корня уравнения , т.е. такое значение , для которого справедливо неравенство , где .

Обычно задача отыскания корня уравнения решается в два этапа.

1-й этап — локализация корня (построение отрезка локализации или построение начального приближения коря). Если — отрезок локализации, то его середину можно считать приближенным значением корня, вычисленным с погрешностью, равной половине длины отрезка локализации. Т.е. если — отрезок локализации, то — приближенное значение корня, , — погрешность корня и — оценка погрешности вычисленного приближенного значения корня.

2-й этап — итерационное уточнение корней на отрезке локализации. Полагаем начальное (нулевое) приближение корня равным середине или одному из концов отрезка локализации:, или .

Затем строим последовательность приближенных значений корня (последовательные итерации), сходящуюся к точному значению корня. Т.е. при , . При этом , поскольку и f(x) непрерывна на отрезке локализации. Как только , то полагаем , т.е. — приближенное значение корня, вычисленное с погрешностью .

Итерационные методы отыскания корней уравнения отличаются друг от друга способами построения итерационной последовательности . Если для вычисления очередной итерации используются только значения и , то итерационный метод называется одношаговым. В противном случае — многошаговым. Поскольку значение неизвестно, в каждом итерационном методе используется свой критерий окончания итерационного процесса.

Будут рассмотрены: метод бисекций, метод простых итераций, метод Ньютона и некоторые модификации метода Ньютона.

Обусловленность задачи вычисления корня нелинейного уравнения. Итак, рассматривается задача вычисления приближенного значения корня уравнения , локализованного в достаточно малой окрестности точного значения корня . Функцию полагаем достаточно гладкой на промежутке локализации. Следовательно, исходные данные задачи — значения в рассмотренной окрестности. Будем полагать, что для приближенных (с учетом погрешностей округления) значений функции справедливо неравенство , — граница абсолютной погрешности вычисления функции.

Для непрерывной существует такая малая окрестность корня , в которой справедливо неравенство .

В этой окрестности значения и неразличимы. Это означает, что невозможно установить в какой точке окрестности значение обращается в нуль. Именно поэтому интервал называется интервалом неопределенности корня . Наша задача состоит в оценке ширины этого интервала — в оценке величины .

Пусть — простой корень уравнения и : , .

По теореме Лагранжа о конечных приращениях .

А поскольку , то имеем , (неравенства приближенные).

Следовательно, , т.е. .

Понятно, что величина — абсолютное число обусловленности задачи вычисления простого корня нелинейного уравнения .

Если — корень уравнения , а — корень уравнения , то и выполнено неравенство , т.е. длина интервала неопределенности и .

Ясно видно, что с уменьшением растет число обусловленности, растет , увеличивается интервал неопределенности.

Этот последнее рассуждение становится очевидным, если рассмотреть на графике поведение в окрестности корня быстро и медленно меняющихся функций.

Обусловленность задачи вычисления кратного корня уравнения. Разложив в окрестности кратного корня кратности k по формуле Тейлора до членов порядка k, имеем

,

тогда

и

.

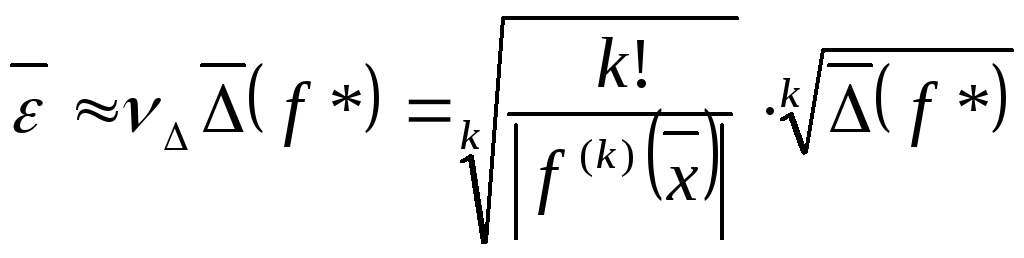Чрезвычайно важно понимать, что , где — машинное эпсилон, погрешность представления в компьютере числа x. Важно понимать, что — наибольшая достижимая точность вычисления корня и бессмысленно уточнять корень после того, как очередное приближение попало в интервал неопределенности. На практике оценить величину достаточно сложно. Для определения этого момента предназначено правило Гарвика:

последовательные итерации выполняются до тех пор, пока они далеки от интервала неопределенности, т.е. пока остается меньше 1, как только становится больше единицы следует прекратить вычисления, исследовать причину увеличения и если устранить ее не удается, положить приближенное значение корня равным ;полученное таким способом решение — наилучшее из возможных.

Метод бисекций

Пусть требуется найти корень уравнения , непрерывная функция.

Предположим, что найден отрезок локализации [a, b] такой, что . Тогда, согласно теореме Больцано – Коши, внутри [a, b] существует точка , в которой значение функции равно нулю, . Требуется найти приближенное значение x* корня уравнения с погрешностью, не превышающей .

Итерационный метод бисекций состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков: , , , n = 0, 1, ….

Каждый последующий отрезок получается делением пополам предыдущего отрезка. Для того чтобы найти корень с погрешностью , деление пополам продолжаем до тех пор, пока длина отрезка не станет меньше .

Опишем один шаг итераций. Пусть на (n -1)-м шаге найден отрезок , такой, что и .

Делим отрезок его пополам точкой и вычисляем . Если или ,то вычисления заканчиваются и — искомое приближенное значение корня. Если же , то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:

если , то ,

если , то .

Описанный процесс построения вложенных отрезков позволяет найти корень уравнения как предел последовательности середин вложенных отрезков , .

Поскольку , метод сходится со скоростью геометрической прогрессии со знаменателем , для достижения заданной погрешности , , следует выполнить шагов (половинных делений).

Понятно, что деления пополам имеет смысл проводить до тех пор, пока значения и "различимы", т.е. пока , т.е. нельзя требовать погрешности, превышающей половину длины интервала неопределенности.

Метод бисекций обладает высокой надежностью, поскольку гарантирует достижение требуемой точности вычислений (она не должна превышать половины длины интервала неопределенности). Метод допускает простую геометрическую интерпретацию.

Метод простых итераций

Функция непрерывна на отрезке локализации [a, b], ; требуется найти приближенное значение x* единственного на [a, b] корня уравнения с погрешностью, не превышающей .

Преобразуем уравнение к виду удобному для итераций.

Метод простых итераций состоит в построении итерационной последовательности , , n = 0, 1, …, , поскольку для непрерывной функции справедливо .

Справедливо следующее утверждение.

Теорема 3.2. Если функция определена и дифференцируема на [a, b], все ее значения принадлежат [a, b], и существует такое число q, что на [a, b], то при любом начальном приближении из [a, b] последовательность , n = 0, 1, …, сходится к единственному на [a, b] корню уравнения , .

При этом и если на [a, b], то , а если на [a, b], то .

Доказательство теоремы

,

,

,

,

.

Величину q в практических задачах оценить не просто. Можно положить

.

Опишем один шаг итераций.

Пусть на (n -1)-м шаге найдено значение . Вычисляем . Если , то полагаем и выполняем очередную итерацию. Если же , то вычисления заканчиваем, полагая . При этом, если , то погрешность приближенного корня не превышает , а если , то погрешность приближенного корня не превышает .

Следовательно, если , то требуемая точность достигнута. Отсюда — условие окончания итерационного процесса:

Итерации заканчиваются, когда и .