Численные методы (Шапошникова Д.А.) / Лекции / Лекция_2_ИЭТ 2011

Методы вычислений. ИЭТ. 4-й семестр. Лекция 2. Стр. 12

МЕТОДЫ ВЫЧИСЛЕНИЙ

ИЭТ, 4-й семестр, 2²

Лекция 2

Введение в элементарную теорию погрешностей: источники и классификация погрешностей численного решения задачи, приближенные числа, абсолютная и условная погрешности, погрешности арифметических операций, погрешность функции.

Приближенные числа. Абсолютная и относительная погрешности

Пусть a — точное значение некоторой величины (как правило, оно неизвестно), a* — приближенное значение величины a.

Ошибка, погрешность, приближенного числа a* — a - a*.

Абсолютная погрешность a* — .

Относительная погрешность a* — .

Их вычислить, как правило, невозможно (a неизвестно), реально полагают .

Теоретическая задача анализа погрешности состоит в оценке границ, погрешностей и : и .

Запись приближенных чисел

Обычно приближенные числа записываются в виде конечной десятичной дроби:

Мы будем использовать «нормализованную» или, как последнее время принято говорить, «научную» форму записи чисел:

Пример. a* = 3.14 = 310⁰+110^-1+410^-2 или a* = 0.31410¹ = 0.31410,

n = 0, .

Значащими цифрами числа a* называются все цифры его записи, начиная с первой ненулевой.

Пример. У числа a* = 0.0103 три значащие цифры (выделены) а у числа b*=0.0103000 — шесть значащих цифр.

Значащую цифру числа a* называют верной, если абсолютная погрешность числа a* не превышает единицы разряда, соответствующего этой цифре.

Пример. Если , то у числа a* = 0.0103000 четыре верных значащих цифры (выделены), а у числа b* = 0.0103 — все значащие цифры верные.

Пример. a = 1.00000, a* = 0.99999, тогда и все значащие цифры числа a* = 0.99999 верные.

Пример. a* = 3.14, .

Количество верных значащих цифр числа тесно связано с его относительной погрешностью:

• если число a* содержит N верных значащих цифр, то ;

• для того, чтобы число a* содержало N верных значащих цифр, достаточно, чтобы ;

• если число a* имеет ровно N верных значащих цифр, то , т.е. — величина порядка .

Эти утверждения позволяют нам в дальнейшем указывать точность числа по числу верных значащих цифр, а потерю точности объяснять как потерю верных знаков.

Границы погрешностей принято записывать с 1-2 значащими цифрами. Большая точность бессмысленна и, следовательно, безграмотна.

Приближенные числа принято записывать в виде . Если число приводится без указания величины погрешности, то принято считать, что все цифры в его записи верные.

Важно понимать, что записи или означают, что на самом деле о величине a известно только то, что ее значение находится в интервале , который естественно называть интервалом неопределенности. Числа , указывают с одинаковым числом цифр после десятичной точки. Используя границу относительной погрешности число принято записывать в виде .

Если число a* приводится без указания величины погрешности, то принято считать, что все цифры в его записи верные и, следовательно, его погрешность не превосходит единицы разряда последней цифры (единицы «младшего» разряда).

Пример. Если число содержит 3 верные значащие цифры, то его относительная погрешность не превышает 10^—3+1 =10^—2 = 1%. Для того, чтобы число содержало 3 верных значащих цифры, его нужно вычислять с относительной погрешностью, не превышающей 10^-3.

Пример. Известно, что число . Часто используется его приближенное значение . Тогда , . Можно считать иначе:

, и .

Округление приближенных чисел

Округление — замена приближенного числа другим числом с меньшим количеством значащих цифр. Округление усечением и округление по дополнению.

Усечение состоит в отбрасывании всех цифр, расположенных справа от n-ой значащей цифры.

Округление по дополнению содержит три правила:

1. Если первая из отбрасываемых цифр больше чем 5, то последняя из сохраняемых увеличивается на 1.Увеличение на единицу совершается и тогда, когда первая отбрасываемая цифра равна 5, а за ней есть одна или несколько значащих цифр. Округляем до трех значащих цифр и

2. Если первая из отбрасываемых цифр меньше 5, то усиление не делается. Округляем до единиц

3. Если отбрасываемая цифра 5, а за ней нет значащих цифр, то последняя цифра остается неизменной, если она четная и увеличивается на 1 , если она нечетная. Округляем до третьего десятичного знака и .

Установить какое округление применяется в используемом математическом обеспечении можно из документации или экспериментально (лучший пример — десятичная запись числа 2/3). Mathcad использует округление по дополнению.

Особенности машинной арифметики

При записи чисел в памяти компьютера может быть использовано только конечное, одно и то же для всех чисел одного класса (целые, действительные, комплексные) число знаков. Отсюда следует, что десятичные числа¹, введенные в память компьютера, содержат ошибку представления.

На большинстве современных компьютеров принята следующая форма записи действительных чисел с плавающей точкой:

,

— двоичные числа, равные 0 или 1, , число — мантисса числа x, целое p — порядок, t — разрядность, . Запись десятичного числа в памяти компьютера, для мантиссы t позиций, для порядка — l, плюс две позиции для знака числа и для знака порядка:

…

…

Отсюда следует:

• в памяти компьютера представимо только конечное число действительных чисел; для всех остальных — округленное значение, т.е. такие числа после ввода в память компьютера содержат ошибку — ошибку представления, она называется ; машинным эпсилон, относительной точностью компьютера, машинной точностью, обозначают , ; границу относительной ошибки представления можно вычислить:

если , то ;

• диапазон представления действительных чисел ограничен; , , — машинный нуль, числа меньшие по модулю чем компьютер не различает и полагает нулем; получение числа x для которого называют исчезновением порядка; не следует путать и , ;. — машинная бесконечность, , получение числа x для которого называют переполнением; для IBM PC t = 23, , , ; для инженеров важно понимать, что мантисса имеет разрядность, эквивалентную 7-14 десятичных разрядов;

• на машинной числовой оси действительные числа расположены неравномерно

поскольку расстояние между двумя ближайшими числами равно 2^p-t и, следовательно, увеличивается с ростом p;

• при выполнении арифметических операций с действительными числами , , , .

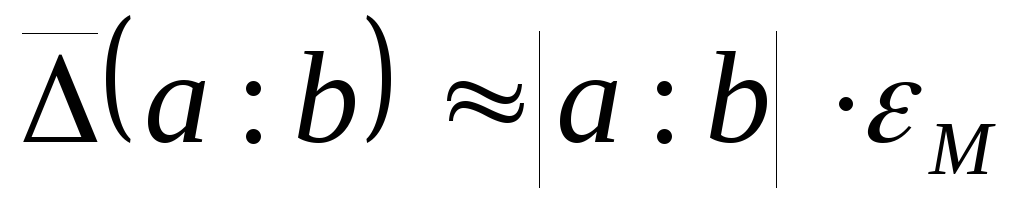Погрешности арифметических операций

Следует обратить внимание на то, что в приведенных выше неравенствах даны оценки границ погрешностей.

Справедливы следующие оценки:

, a>0, b>0,

, ,

,

, .

Докажем некоторые оценки (остальные оценки получаются аналогично).

,

. Из последней оценки видно, что при больших значениях , т.е. при вычитании близких чисел возможна «катастрофическая потеря точности».

Заметим, что если , то вместо оценок , .

можно полагать , .

Наибольшая потеря точности происходит при вычитании близких чисел одного знака, потеря точности не происходит при сложении чисел одного знака.

Погрешность вычисления функции одного переменного

Пусть — дифференцируемая в области G (на некотором интервале, содержащем x и x*) функция, x* — приближенное значение аргумента, — приближенное значение функции, — соответствующие погрешности. Оценку погрешности можно получить из формулы конечных приращений Лагранжа: т.е. обычно полагают

Отсюда нетрудно получить оценку границы относительной погрешности вычисления функции: .

Для функции, заданной неявно : и

,.

Погрешность вычисления функции нескольких переменных

Пусть — дифференцируемая в области G функция, 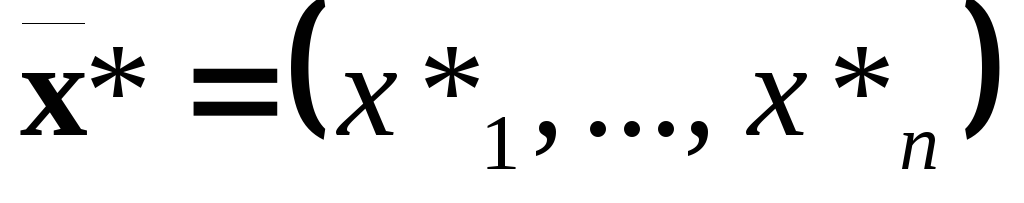— приближенное значение аргумента, — приближенное значение функции, — соответствующие погрешности. Оценку погрешности можно получить из формулы конечных приращений Лагранжа:

т.е. обычно полагают .

Отсюда нетрудно получить оценку границы относительной погрешности вычисления функции: .

Для функции, заданной неявно :

,.

Если заданная погрешность результата приближенных вычислений , то обычно рекомендуют выполнять промежуточные вычисления с двумя-тремя дополнительными знаками, т.е. с погрешностью порядка .

Аналогично поступаем в случаях, когда исходные данные задачи содержат погрешности порядка

1 целые числа обсуждаются отдельно, это обсуждение вне рамок нашего курса