
Численные методы (Шапошникова Д.А.) / Лекции / Лекция_8_ИЭТ 2011 Интерполяция сплайнами
.docМетоды
вычислений. ИЭТ. 4-й семестр. Лекция 8.
Стр.
МЕТОДЫ ВЫЧИСЛЕНИЙ
ИЭТ, 4-й семестр, 22
Лекция 8
Интерполяция сплайнами
Интерполяция сплайнами, метод наименьших квадратов.
На
практике часто возникает задача
интерполяции с наперед заданными узлами
интерполяции и, следовательно, улучшить
свойства интерполяции построением
многочлена наилучшего равномерного
приближения невозможно. Тогда, вместо
построения глобального интерполяционного
полинома на всем промежутке, используют
интерполяцию "кусочными многочленами".
Простейший пример такой интерполяции
известен всем. Обычно, изображая на
графике экспериментальные точки
![]() ,
их, не задумываясь, соединяют отрезками
прямых. Это ни что иное как кусочная
интерполяция многочленами первой
степени.
,
их, не задумываясь, соединяют отрезками
прямых. Это ни что иное как кусочная
интерполяция многочленами первой
степени.
В
общем случае отрезок
![]() точками
точками
![]() разбивают на части и на каждом отрезке
разбивают на части и на каждом отрезке
![]() строят некоторый интерполяционный
многочлен. Такой многочлен-многозвенник
дает интерполяцию на всем отрезке и
называют сплайном.
Свойства сплайна будут зависеть от
степени многочлена на каждом отрезке
(обычно они одинаковы для всех отрезков)
и от условий на концах отрезков. Гладкие
сплайны обладают многими замечательными
свойствами, которые обеспечили им
широкое применение в прикладных
вычислениях. Например, кубический сплайн
функции Рунге на сетке с шестью узлами
дает настолько малую погрешность, что
она не видна на графике.
строят некоторый интерполяционный
многочлен. Такой многочлен-многозвенник
дает интерполяцию на всем отрезке и
называют сплайном.
Свойства сплайна будут зависеть от
степени многочлена на каждом отрезке
(обычно они одинаковы для всех отрезков)
и от условий на концах отрезков. Гладкие
сплайны обладают многими замечательными
свойствами, которые обеспечили им
широкое применение в прикладных
вычислениях. Например, кубический сплайн
функции Рунге на сетке с шестью узлами
дает настолько малую погрешность, что
она не видна на графике.
Опр.
Пусть отрезок
![]() разбит точками
разбит точками
![]() на N
частичных отрезков
на N
частичных отрезков
![]() .
Сплайном
степени
m
называется
функция
.
Сплайном
степени
m
называется
функция
![]() ,
обладающая следующими свойствами:
,
обладающая следующими свойствами:
-
функция
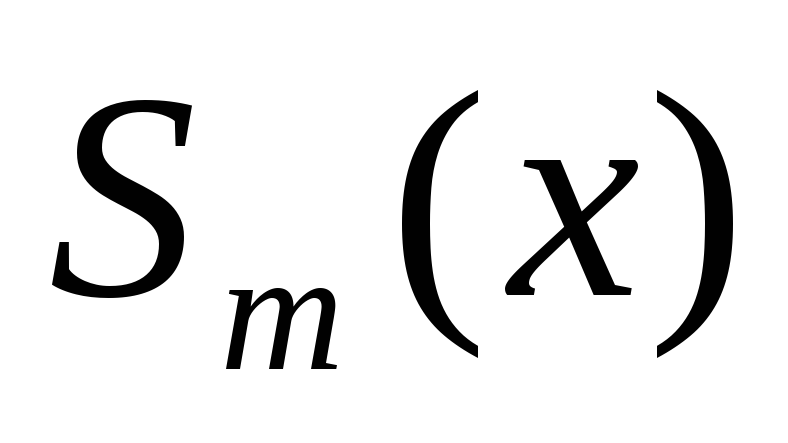 непрерывна на отрезке
непрерывна на отрезке
 вместе со всеми своими производными
вместе со всеми своими производными
 до некоторого порядка р.
до некоторого порядка р. -
на каждом частичном отрезке
 функция
функция
 совпадает некоторым алгебраическим
многочленом степени m.
Разность m-p
между степенью сплайна и наивысшим
порядком непрерывной отрезке
совпадает некоторым алгебраическим
многочленом степени m.
Разность m-p
между степенью сплайна и наивысшим
порядком непрерывной отрезке
 производной называется дефектом
сплайна.
производной называется дефектом
сплайна.
Наиболее широкое применение получили кубические сплайны— дважды непрерывно дифференцируемые сплайны, с дефектом равным 1, построенные с использованием кусочной интерполяции многочленами третьей степени.
Такие
сплайны на каждом из частичных отрезков
![]() совпадают с кубическим многочленом:
совпадают с кубическим многочленом:
![]()
Пусть
некоторая дважды непрерывно дифференцируемая
функция
![]() задана
на отрезке
задана
на отрезке
![]() своими значениями в узлах сетки
своими значениями в узлах сетки
![]() .
.
Интерполяционным
кубическим сплайном
![]() ,
с дефектом равным 1,
называется
сплайн, удовлетворяющий условиям:
,
с дефектом равным 1,
называется
сплайн, удовлетворяющий условиям:
-
 ,
для
,
для
 .
Количество условий
.
Количество условий

-
 -наклон
сплайна в точке
-наклон
сплайна в точке
 ,
,
 .
Количество условий
.
Количество условий
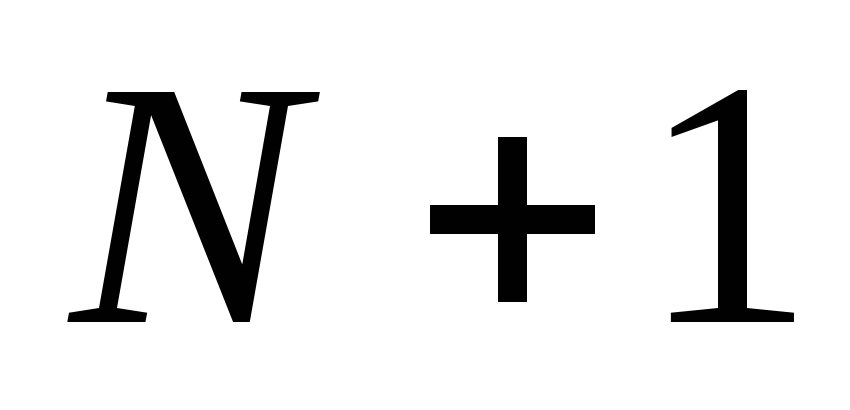
-
 ,
,
 .
Количество условий
.
Количество условий

-
 ,
,
 .
Количество условий
.
Количество условий

-
Одному из граничных условий
 .
Количество условий 2.
.
Количество условий 2.
Воспользуемся
последними из них, так называемыми
"естественными условиями", опишем
задачу, вычисления сплайна. На каждом
из отрезков
![]() будем записывать сплайн в виде
будем записывать сплайн в виде
![]() .
Тогда
.
Тогда
![]() а,
а,
![]()
Для
вычисления его
![]() коэффициентов
требуется записать
коэффициентов
требуется записать
![]() уравнения. Производные сплайна вычисляем
аналитически — для производных функции
уравнения. Производные сплайна вычисляем
аналитически — для производных функции
![]() во внутренних узлах используем формулы
центральных разностных производных
во внутренних узлах используем формулы
центральных разностных производных
![]() ,
в точке a
— правую разностную производную
,
в точке a
— правую разностную производную
![]() ,
а точке b
— левую —
,
а точке b
— левую —
![]() .
Имеем
.
Имеем
![]() равенство значений функции и сплайна
в узлах сетки,
равенство значений функции и сплайна
в узлах сетки,
![]() уравнений непрерывности сплайна и его
первых и вторых производных во внутренних
узлах сетки и еще 2 уравнения из
естественных граничных условий, т.е.
имеем систему
уравнений непрерывности сплайна и его
первых и вторых производных во внутренних
узлах сетки и еще 2 уравнения из
естественных граничных условий, т.е.
имеем систему
![]() уравнений относительно
уравнений относительно
![]() неизвестных коэффициентов. Относительно
этой системы известно, что система имеет
невырожденную трех диагональную матрицу.
Единственное решение системы находят
специальным методом решения систем с
трехдиагональными матрицами — методом
прогонки.
неизвестных коэффициентов. Относительно
этой системы известно, что система имеет
невырожденную трех диагональную матрицу.
Единственное решение системы находят
специальным методом решения систем с
трехдиагональными матрицами — методом
прогонки.
Теорема
1. Пусть
функция
![]() имеет отрезке
имеет отрезке
![]() непрерывную производную четвертого
порядка и
непрерывную производную четвертого
порядка и
![]() .
Тогда для интерполяционного кубического
сплайна
.
Тогда для интерполяционного кубического
сплайна![]() , удовлетворяющего граничным условиям
типов I.,
II.,
III.,
IV,
справедлива следующая оценка погрешности:
, удовлетворяющего граничным условиям
типов I.,
II.,
III.,
IV,
справедлива следующая оценка погрешности:
![]() .
.
Приведем
пример построения квадратичного
(параболического) сплайна для функции![]() ,
заданной таблицей своих значений, с
дополнительным условием S’(1)=2
,
заданной таблицей своих значений, с
дополнительным условием S’(1)=2
|
x |
1 |
2 |
3 |
6 |
|
y |
2 |
5 |
10 |
6 |





Вычислив однажды коэффициенты сплайна, можно в дальнейших вычислениях заменять значения функции значениями сплайна, поскольку программы, реализующие вычисления сплайна имеют метку для повторного обращения. Т.е. при последующих обращениях производится вычисление приближенного значения функции (значения сплайна) по вычисленным при первом обращении коэффициентам сплайна, и вычисления организованы так, что погрешности округления минимальны.
Аппроксимация данных методом наименьших квадратов
Пусть функция
![]() задана таблицей приближенных значений
задана таблицей приближенных значений
 ,
полученных с ошибками
,
полученных с ошибками
![]() .
В этом случае требование
.
В этом случае требование
![]() для аппроксимирующей функции
для аппроксимирующей функции
![]() может привести к неоправданным
дополнительным погрешностям. Выберем
другой подход. Будем использовать для
аппроксимации функции
может привести к неоправданным
дополнительным погрешностям. Выберем
другой подход. Будем использовать для
аппроксимации функции
![]() линейную модель
линейную модель
![]() ,
где
,
где
![]() — заданные базисные функции, а
— заданные базисные функции, а
![]() — параметры модели, коэффициенты
обобщенного многочлена.
— параметры модели, коэффициенты
обобщенного многочлена.
Отказываясь от
требования выполнения в точках
![]() точных равенств, следует все же стремится
к тому, чтобы в этих точках выполнялись
соответствующие приближенные равенства
точных равенств, следует все же стремится
к тому, чтобы в этих точках выполнялись
соответствующие приближенные равенства
![]() .
.
Наиболее часто
используется линейная модель с базисными
функциями
![]() .
.
Система приближенных равенств:
 относительно
коэффициентов многочлена
относительно
коэффициентов многочлена![]()
Одним из критериев
выбора параметров
![]() линейной модели является критерий
наименьших квадратов: параметры выбирают
так, чтобы среднеквадратичное отклонение
линейной модели является критерий
наименьших квадратов: параметры выбирают
так, чтобы среднеквадратичное отклонение
![]() было минимальным. Ясно, что минимум
среднеквадратичного отклонения
достигается в той же точке, что и минимум
функции
было минимальным. Ясно, что минимум
среднеквадратичного отклонения
достигается в той же точке, что и минимум
функции

![]()
В силу необходимого
условия экстремума функции нескольких
переменных параметры линейной модели
удовлетворяют условию
![]() .
Посчитаем частную производную функции
.
Посчитаем частную производную функции
![]() по
по
![]() :
:
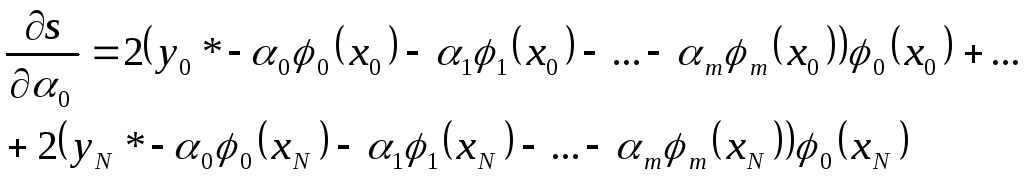
После несложных
вычислений получаем нормальную
систему метода наименьших квадратов
 ,
,
![]() .
.
Доказано, что для
линейно независимых базисных функций
система имеет единственное решение.
Очевидно, что в случае
![]() и
и
![]() ,
,
![]() совпадает с интерполяционным многочленом.
Однако метод наименьших квадратов
обычно применяют при
совпадает с интерполяционным многочленом.
Однако метод наименьших квадратов
обычно применяют при
![]() .
.
В случае приближения
алгебраическими многочленами
![]() нормальная система принимает следующий
вид:
нормальная система принимает следующий
вид:
 ,
,
![]()
Запишем систему в развернутом виде в двух наиболее простых случаях m=1,m=2.
-
m=1, приближение осуществляется многочленом 1-ой степени P1(x)=a0+a1x, нормальная система имеет вид:

-
m=2, используется многочлен 2-ой степени P1(x)=a0+a1x+a2x2, нормальная система имеет вид:
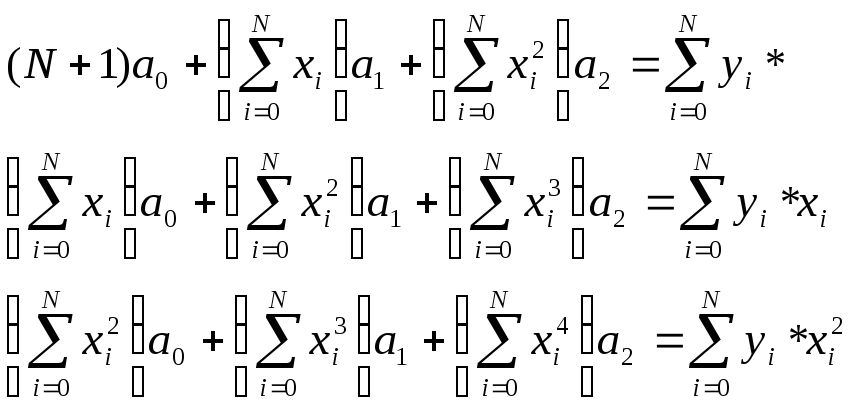
Рассмотрим пример. Пусть функция
![]() задана таблицей своих значений
задана таблицей своих значений
|
x |
-1 |
0 |
1 |
2 |
|
y |
1 |
3 |
2 |
5 |
Используя метод
наименьших квадратов, аппроксимируем
ее многочленами первой и второй степени
и найдем соответствующие среднеквадратичные
уклонения
![]() .
.
Вычислим коэффициенты и правые части нормальных систем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Для многочлена первой степени нормальная система имеет вид
![]() , решив ее, получим
значения
, решив ее, получим
значения
![]()
Рисунок многочлена P1(x)=2.2+1.1x наилучшего среднеквадратичного приближения:
 Средне квадратичное уклонение вычислим
по формуле:
Средне квадратичное уклонение вычислим
по формуле:

Для многочлена второй степени нормальная система имеет вид
 , решив ее, получим
значения
, решив ее, получим
значения
![]()
Рисунок многочлена P1(x)=1.95+0.85x+0.25 x2 наилучшего среднеквадратичного приближения:
 Средне квадратичное уклонение вычислим
по формуле:
Средне квадратичное уклонение вычислим
по формуле:

Нормальную систему метода наименьших квадратов можно получить из других соображений.
Рассмотрим
несовместную линейную систему
![]() ,
,
![]() ,
,
![]() .
Если причина несовместности системы
заключена в том, что элементы матрицы
системы и/или правые части содержат
ошибки, то задача об отыскании ее
приближенного решения имеет смысл.
Несовместность системы означает, что
вектор
.
Если причина несовместности системы
заключена в том, что элементы матрицы
системы и/или правые части содержат
ошибки, то задача об отыскании ее
приближенного решения имеет смысл.
Несовместность системы означает, что
вектор
![]() не принадлежит линейному пространству
столбцов матрицы А.
Назовем нормальным
обобщенным решением
несовместной системы
не принадлежит линейному пространству
столбцов матрицы А.
Назовем нормальным
обобщенным решением
несовместной системы
![]() такой вектор
такой вектор
![]() ,
для которого коэффициенты невязка
,
для которого коэффициенты невязка
![]() минимальна. Из линейной алгебры (или из
геометрических соображений (см. рис.))
понятно, что невязка минимальна тогда
и только тогда, когда вектор
невязки
минимальна. Из линейной алгебры (или из
геометрических соображений (см. рис.))
понятно, что невязка минимальна тогда
и только тогда, когда вектор
невязки
![]() ортогонален пространству столбцов
матрицы А:
ортогонален пространству столбцов
матрицы А:
![]() или, что то же самое,
или, что то же самое,
![]() для всех
для всех
![]() .
Известно, что единственный вектор,
ортогональный всем векторам пространства
.
Известно, что единственный вектор,
ортогональный всем векторам пространства
![]() — нулевой вектор, т.е.
— нулевой вектор, т.е.
![]() ,
откуда
,
откуда
![]() .
.
Эта последняя система и есть нормальная система метода наименьших квадратов.
Пример.
Вернемся к задаче аппроксимации функции.
Для простоты записи ограничимся случаем
линейной аппроксимации линейными
функциями:![]() ,
,
![]() .
.
Если потребовать
точного выполнения равенств
![]() ,
то получим систему N
линейных
уравнений относительно двух неизвестных
,
то получим систему N
линейных
уравнений относительно двух неизвестных
![]() ,
,
![]() ,
с матрицей
,
с матрицей
 , правой частью
, правой частью
![]() и вектором неизвестных
и вектором неизвестных
![]() .
Нормальная система метода наименьших
квадратов в этом случае —
.
Нормальная система метода наименьших
квадратов в этом случае —
 .
Если все узлы
.
Если все узлы
![]() различны, матрица
различны, матрица
![]() обратима и искомое решение определяется
равенством
обратима и искомое решение определяется
равенством
 .
Заметим, что нормальная система метода
наименьших квадратов часто оказывается
плохо обусловленной.
.
Заметим, что нормальная система метода
наименьших квадратов часто оказывается
плохо обусловленной.

