Численные методы (Шапошникова Д.А.) / Лекции / Лекция_13-14_ИЭТ 2011

Методы вычислений. ИЭТ. 4-й семестр. Лекция 13. Стр. 5

МЕТОДЫ ВЫЧИСЛЕНИЙ

ИЭТ, 4-й семестр, 2²

Лекция 13

Методы одномерной оптимизации. Обусловленность задачи одномерной минимизации.

Прямой и пассивный поиск. Метод дихотомии, метод золотого сечения, метод Ньютона

Минимизация функции одной переменной имеет самостоятельный интерес и является важным элементом различных процедур минимизации функции нескольких переменных. От правильной организации одномерного поиска зачастую зависит успех всей задачи многомерной минимизации. Именно поэтому рассмотрим методы одномерной минимизации подробнее, нежели методы многомерной минимизации.

Основные понятия и обозначения. Простановка задачи. Пусть — функция одной переменной, определенная на множестве . Точка называется точкой глобального минимума функции , если для всех . В этом случае — минимальное значение функции. Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что неравенство справедливо для всех . Если дифференцируема на , то необходимым условием локального минимума является условие и точка, в которой выполнено это условие, называется стационарной точкой. Если же дважды непрерывно дифференцируема на , то неравенство — достаточное условие того, что стационарная точка является точкой минимума.

Подобно тому, как при решении нелинейных уравнений реально рассматривалось отыскание одного изолированного корня, так и при одномерной минимизации будем рассматривать только алгоритмы отыскания локального минимума. Следовательно, как и при решении уравнений возникает необходимость локализации минимума. Здесь, как и при локализации корней уравнения, отсутствуют регулярные методы отыскания отрезка локализации. Поможет "здравый смысл" и априорная информация о целевой функции (так в задачах оптимизации называют функцию ). Будем в дальнейшем предполагать, что минимум локализован на отрезке .

Методы отыскания минимума называют методами поиска. Если метод состоит в сравнении значений функции в точках , то его называют методом прямого поиска, а точки называют пробными точками.

Различают пассивный и последовательный поиск. Методом пассивного поиска, называется метод, в котором все пробные точки вычислены заранее и точка минимума отыскивается среди них. Метод называется методом последовательного поиска, если для вычисления очередной пробной точки используется информация о значениях функции в вычисленных ранее пробных точках. Будем предполагать обычно (если не оговорено иное), что количество N пробных точек на отрезке локализации фиксировано.

Функция называется унимодальной на отрезке , если на этом отрезке содержится единственная точка минимума. Заметим, что унимодальная функция не должна быть гладкой, она может даже не быть непрерывной. Из определения унимодальности следует, что если , то . Аналогично, если , то . Для сужения отрезка локализации полезны следующие свойства унимодальной функции. Пусть унимодальна на отрезке и . Тогда:

если , то ;

если , то ;

если и , то .

Для унимодальной функции задача отыскания минимума имеет единственное решение. Для непрерывной унимодальной функции она корректна.

Обусловленность задачи минимизации. Пусть — точка локального минимума функции , вычисленной с погрешностью . Ясно, что существует такая окрестность (назовем ее интервал неопределенности), для которой, по значениям нельзя достоверно определить точку минимума функции.

Пусть дважды непрерывно дифференцируема в окрестности точки минимума , и . Тогда вблизи справедливо .

Найдем наименьшее расстояние , для которого заведомо выполнено :

и справедливо, если . Т.е. .

Отсюда следует, что задачу минимизации нельзя считать хорошо обусловленной.

Если задача "хорошо масштабирована", т.е. , , то в терминах относительных погрешностей . Это означает, что если , то , т.е. приближенное значение точки минимума можно найти только с половиной верных значащих цифр значения функции. При вычислении точки минимума происходит потеря половины верных значащих цифр.

Заметим, что хотя задача отыскания минимума эквивалентна задаче о решении нелинейного уравнения , эта последняя задача менее чувствительна к погрешностям округления, поскольку для нее справедлива оценка .

Методы прямого поиска. Оптимальный пассивный поиск. Метод прямого пассивного поиска состоит в сравнении значений функции в пробных точках . За приближенное значение точки минимума принимают то значение , для которого значение функции является наименьшим. Тогда, очевидно, .

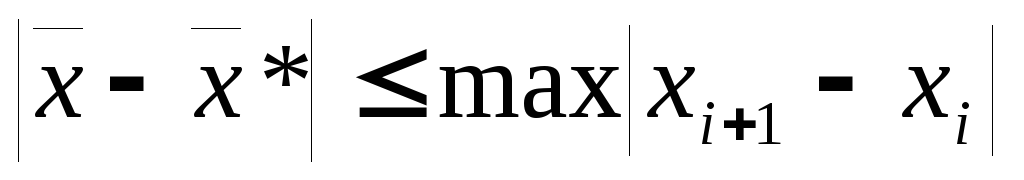Очевидно, что погрешность минимальна, если пробные точки образуют равномерную сетку на отрезке локализации. Имеет место оптимальный пассивный поиском:

, , , , .

Последовательный поиск. Метод дихотомии

(метод половинного деления пополам)

Метод половинного деления состоит в построении множества (N-1) вложенных отрезков локализации, пробные точки расположены вблизи середины очередного отрезка локализации:

, , , ;

если , то и ,

если , то и .

При этом и при стремиться к величине , т.е.

только при . Т.е. вычисления прекращаются, как только . Поскольку значения функции вычисляются приближенно, то для того чтобы знак разности совпадал со знаком разности , необходимо, чтобы , т.е. нельзя выбирать слишком малым.

Заметим, что в методе половинного деления на каждом шаге значения функции вычисляются в двух точках, и .

Последовательный поиск. Метод золотого сечения

Говорят, что внутренняя точка отрезка является точкой золотого сечения, если она делит отрезок на две неравные части так, что отношение длины большей из них к длине меньшей равно отношению длины всего отрезка к длине большей его части. Иногда именно величину этого отношения называют "золотым сечением".

Легко проверить, что точки и осуществляют золотое сечение отрезка .

Метод золотого сечения состоит в построении множества (N-1) вложенных отрезков локализации, пробные точки делят предыдущий отрезок в отношении, которое определяется золотым сечением:

, , , , ,

если , то и ,

если , то и .

Здесь точка совпадает с точкой или с точкой . Поэтому на очередном шаге достаточно вычислить значение функции только в одной точке.

При этом через (N-1) шагов и .

Рассмотрены наиболее популярные методы одномерной минимизации. Другая группа методов — модификации методов решения нелинейных уравнений, которые применяются к решению уравнения .

Дополнительные материалы к лекции 7

Последовательный поиск. Метод Фибоначчи.

Числа Фибоначчи: , , , . Последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Метод Фибоначчи, как и метод половинного деления, состоит в построении множества (N-1) вложенных отрезков локализации, пробные точки делят предыдущий отрезок в отношении, которое определяется числами Фибоначчи:

, , , , ,

если , то и ,

если же , то и .

Здесь важно, что на очередном шаге итераций точка совпадает с или с . Поэтому на очередном шаге достаточно вычислить значение функции только в одной недостающей точке.

При этом через (N-1) шаг и . Определив из этого условия значение N, выполняем последовательный поиск методом Фибоначчи. Заметим, что в методе Фибоначчи на каждом очередном шаге отрезок локализации уменьшается в : или , т.е. .

За (N-1) шаг отрезок локализации уменьшится в раз, и приближенное значение точки минимума — середина последнего отрезка локализации. Действительно,

.

Эффективность методов прямого поиска можно сравнивать по тому, на сколько уменьшается отрезок локализации на одном шаге, по количеству вычислений функции за N шагов, по величине гарантированной погрешности:

Название	Длина отрезка локализации	Гарантированная погрешность
Оптимальный пассивный поиск
Половинное деление
Фибоначчи
Золотое сечение

Можно посчитать число шагов, которое нужно выполнить для того, чтобы на отрезке локализации единичной длины найти точку минимума с заданной погрешностью:

Название
Оптимальный пассивный поиск	9	99	999	9999	99999
Половинное деление	6	12	18	26	32
Фибоначчи	5	10	15	19	24
Золотое сечение	5	10	15	20	24