
- •11.1 Методы выращивания кристаллов в электронной технике
- •11.1.1. Методы выращивания твердотельных диэлектрических монокристаллов.
- •11.1.1.1 Общие вопросы кристаллизации из расплава
- •11.1.1.2. Методы выращивания диэлектрических лазерных кристаллов из расплава
- •11.1.1.3. Метод Вернейля
- •11.1.1.4. Метод Чохральского
- •11.1.1.5. Метод горизонтально направленной кристаллизации (метод Багдасарова)
- •11.1.1.6. Meтод вертикально направленной кристаллизации
- •11.1.1.7 Применение индукционного нагрева для выращивания лазерных монокристаллов
- •11.1.1.8.Водоохлаждамые контейнеры в технологии выращивания кристаллов
- •11.1.7.2 Гарнисажный метод выращивания кристаллов
- •11.1.1.8. Новые экспрессные методы выращивания тугоплавких лазерных монокристаллов
- •11.1.2 Выращивание диэлектрических кристаллов из высокотемпературных растворов
- •11.1.2.1. Составы растворителей, используемые для выращивания лазерных кристаллов
- •11.1.2.2. Методы выращивания лазерных кристаллов из высокотемпературных растворов
- •2.10.3 Гидротермальный синтез диэлектрических сплавов
- •11.1.3.1. Общие проблемы гидротермального синтеза
- •11.1.3.2. Основы метода гидротермальной кристаллизации
- •11.1.3.3. Термодинамические и кинетические условия гидротермальной кристаллизации
- •11.1.3.4 Аппаратура и методика эксперимента
- •11.1.3.5. Гидротермальный синтез кристаллов методом температурного перепада
- •11.1.3.6. Гидротермальный синтез кристаллов методов "метастабильной фазы"
11.1 Методы выращивания кристаллов в электронной технике
11.1.1. Методы выращивания твердотельных диэлектрических монокристаллов.
11.1.1.1 Общие вопросы кристаллизации из расплава
Подавляющее большинство кристаллов, нашедших применение в квантовой электронике, выращивается из жидкого состояния, а именно; из расплава или из раствора. Причем кристаллизацией из расплава выращивается более половины технически ценных монокристаллов. Веществами, монокристаллы которых наиболее пригодны для выращивания из расплава, являются те, которые плавятся без разложения, не имеют полиморфных переходов и характеризуются низкой химической активностью по отношению к материалом контейнера, кристаллизатора и газам. Кристаллизация из расплава сопровождается рядом физико-химических процессов, среди которых можно выделить четыре основные группы:
1) процессы, влияющие на состав расплава: термическая диссоциация исходного вещества, его химическое взаимодействие с окружающей средой, испарение продуктов диссоциации и примесей, содержащихся в расплаве;
2) процессы на фронте кристаллизации, определяющие кинетику фазового перехода;
3) процессы теплопереноса, определяющие распределение температуры в кристалле и расплаве;
4) процессы массопереноса, и, в особенности, перенос примесей, обусловленный конвекцией и диффузией в расплаве.
В идеальном случае условия кристаллизации определяются при совместном решении точных уравнений, описывающих все четыре группы процессов. Однако на современном уровне развития данного научного направления точное решение уравнений практически невозможно и, как это будет показано в разделе 11.1.4, только для ряда случаев найдено оптимальное приблизительное решение.
Кристаллы из расплава обычно растут либо по механизму нормального, либо послойного роста. Часто при кристаллизации действуют оба эти механизма. Присоединение атомов к "атомно-шероховатой поверхности (по механизму нормального роста) с макроскопической точки зрения происходит в любом месте так что растущая поверхность перемешается вдоль нормали параллельно самой себе. «Атомно-гладкие» поверхности (послойный рост) растут путем последовательного отложения слоев, т.е. путем тангенциального перемещения ступеней. Движущей силой кристаллизации является стремление системы к минимуму свободной энергии. Изменение средней энергии частицы по мере ее смещения относительно границы-раздела схематично представлено на рис. 11.1.1 где Ек и Ес - средние энергии частиц, занимающих равновесные положения соответственно в кристалле и расплаве.
Р ис.
11.1.1. Средняя энергия атома в окрестности
фазовой Границы
ис.
11.1.1. Средняя энергия атома в окрестности
фазовой Границы
При переходе частицы из кристалла в расплав ее энергия изменится на величину
Ес-Ек=Т0 (Sc-Sк)=∆Н (11.1.1)
где Т0 - температура фазового перехода, S - энтропия. Кроме того она, должна преодолеть потенциальный барьер Е. Энергия активации Е определяется взаимодействием с окружением частицы, совершающей переход из расплава в кристалл.
Число j+ атомов, перешедшие из расплава в кристалл за единицу времени на одном изломе и обратноперешедших из кристаллов в расплав j- записываем согласно схеме на рис, 11.1.1 в следующем виде:
j+=ν exp[-∆S(kT) exp(-E)kT] (11.1.2)
j-=ν exp[-(E+∆H)/kT]
где ν — частота тепловых колебаний атомов в кристалле (расплаве). exp (-∆S/kT)-вероятность пребывания атома расплава у излома в наиболее выгодном состоянии, отвечающему барьеру Еc , Из равенства токов j+=j- при Т=Т0 следует:
∆S=Sc-Sк
Если среднее расстояние между изломами равно λu , то вероятность встретить излом на поверхности равна (а/λu)2. Тогда выражение для скорости перемещения фазовой границы будет иметьвид
V=(а/λu)2· а(j+-j-)=(а/λu)2·а·exp(-E/kT)·exp(-∆S/kT)·
·{1-exp(-∆H/k(1/T-1/T0)]βT∆T}, (11.1.3)
βT=(а/λu)2·а·ν ·∆S/kT·exp(-∆S/kT)·exp(-E/kT)
где β - кинетический коэффициент кристаллизации из расплава, а — параметр ячейки кристалла.
Таким образом, для механизма нормального роста .характерна линейная зависимость скорости от величины переохлаждения. Причем при выращивании по механизму нормального роста достаточны малые значения величин переохлаждения.
В случае послойного роста элементарные ступени отделены друг от друга "атомно-гладкими" участками (рис. 11.1.2), для роста которых требуется образование новых ступеней» При этом требуется большое переохлаждение, чем в случае нормального роста.
Р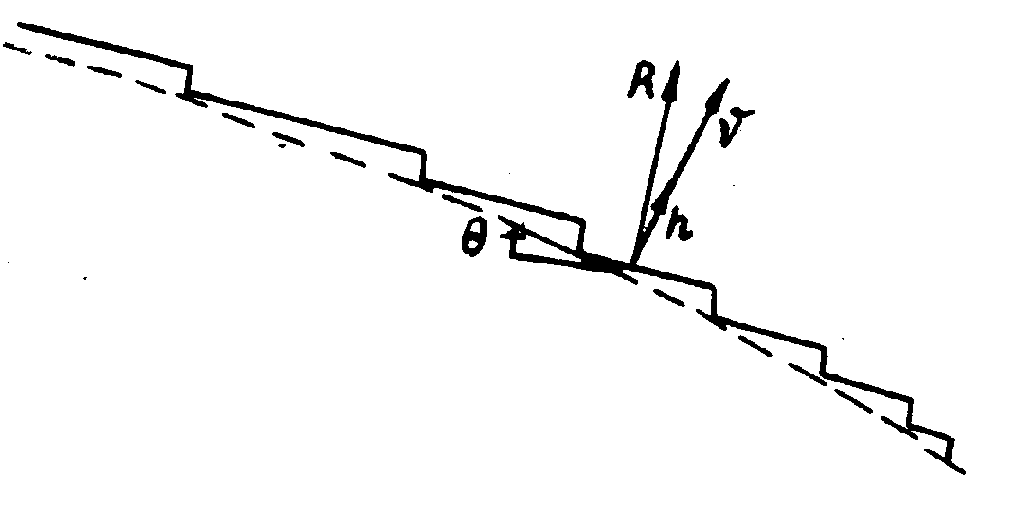 ис.
11.1.2 Ступенчатая поверхность кристалла
(угол характеризует отклонение
ориентации от сингулярной грани, R -
скорость роста поверхности вдоль нормали
к этой грани, V - скорость роста вдоль
нормали n к рассматриваемой поверхности)
ис.
11.1.2 Ступенчатая поверхность кристалла
(угол характеризует отклонение
ориентации от сингулярной грани, R -
скорость роста поверхности вдоль нормали
к этой грани, V - скорость роста вдоль
нормали n к рассматриваемой поверхности)
Если каждая ступень движется вдоль грани со скоростью V, -то вся совокупность ступеней будет характеризоваться некоторой средней скоростью
R = h/L·V =|P|·V (11.1.4)
где L - расстояние между ступенями; h - высота ступени; Р - наклон поверхности к рассматриваемой сингулярной грани (рис. 11.1.2). Таким образом, при послойном росте скорость является функцией параметра Р. Устойчивость и форма фазовой границы определяется процессами теплопереноса. Известно, что эти процессы при кристаллизации могут происходить как за счет теплопроводности, так и путем излучения и конвекции в расплаве (растворе). Учет разных механизмов переноса тепла позволяет выделить три случая:
αL >>1; αL ~ l; αL<<1
где α - коэффициент поглощения в области максимального теплового излучения, L - характеристический размер объема вдоль направления теплового потока. Первый случай соответствует непрозрачным средам, в которых перенос тепла осуществляется только за счет молекулярной теплопроводности. В этом случае распределение температуры описывается уравнением Фурье
q=-χm ∆T (11.1.5)
где q - поток тепла, χm — коэффициент теплопроводности, ∆T — разница температуры.
Второй случай соответствует полупрозрачным средам, т.е. излучение от источника нагрева, попавшее в кристалл, в нем и затухает. Перенос тепла осуществляется путем переиэлучения. В данном случае еще возможно представить поток тепла в виде выражения (11.1.5). Однако под коэффициентом теплопроводности следует понимать сумму
χ=χm + χ p (11.1.6)
χ p=16 n2 σ T3/3α (11.1.7)
где n - показатель преломления, σ - постоянная Стефана—Больцмана.
В общем случае доли молекулярной (χm) и радиационной (χp) составляющих теплопроводности, определяются положением максимума функции Планка относительно полосы пропускания кристалла. В достаточно прозрачных кристаллах при высоких температурах перенос -тепла может полностью определяться, их оптическими свойствами. Третий случай - случай прозрачного кристалла. В процессе роста такого кристалла излучение в нем практически не затухает. На процесс переноса тепла существенное влияние оказывает излучение нагревателя, стекой контейнера и т.п. В этом случае соотношение (11.1.5) не выполняется и уравнениями теплопроводности для описания явления пользоваться нельзя. Их следует заменять интегральными уравнениями переноса лучистой энергии. Коэффициент теплопереноса для прозрачных сред является некоторой эффективной величиной, зависящей от формы и состояния поверхностей, на которых происходит отражение и преломление излучения
λэф=4πлЕ3nψ (11.1.8)
где ψ - фактор, зависящий от оптических свойств к конфигурации системы.
Показано, что существует, например, критическая длина кристалла, определяемая природой материала и радиусом растущего кристалла, после превышения которой тепловой поток через границу раздела фаз становится независимым от длины кристалла. С повышением прозрачности вещества усложняется управление температурными градиентами и главное усложняется поддержание их постоянными на протяжения всего процесса выращивания. В этой связи важную роль играет конвективный перенос в расплаве, который в зависимости от метода выращивания может иметь различный характер. Конвекция в расплаве (в растворе) может быть естественной, обусловленной гравитационной и негравитационной составляющими. Первый тип конвекции может иметь тепловую и концентрационную природу в зависимости от причины, вызывающей изменение плотности жидкости. Второй тип включает в себя термокапилярную и капиллярно—концентрационную конвекции.
Вынужденная конвекция создается искусственно путем механического перемешивания расплава (раствора) с помощью мешалок, вращения и перемещения тигля, а также вращения и перемещения кристаллов, а в ряде случаев вследствие взаимодействия расплава с электромагнитными полями. Гидродинамика расплава при кристаллизации имеет сложный пространственно-временной характер, в связи с чем для ее описания требуется решение общих гидродинамических уравнений, в основе которых лежат уравнения Навье—Стокса. Для того, чтобы достичь возможно большего приближения к идеальному состоянию равномерного роста кристалла в радиально—симметричном температурном поле зоны кристаллизации в ходе всего процесса выращивания, необходимо прежде всего рассмотреть причины нарушения стационарного роста. Это непосредственно приводит к исследованию тепловых процессов, протекающих при выращивании, например, из расплава, поскольку именно они влияют на структурное совершенство выращиваемого кристалла. При изменении температурных условий в ходе процесса выращивания в зоне кристаллизации наблюдаются как долговременные, так и кратковременные эффекты, связанные с изменениями температурного поля. В качестве примера медленно изменяющихся условий роста (порядка нескольких десятков часов) могут служить опускание уровня поверхности расплава, возрастание объема, увеличение боковой поверхности кристалла и т.д. К эффектам с малой постоянной времени относятся прежде всего флуктуации температуры расплава вблизи границы раздела фаз и вызванные ими колебания локальной скорости роста. Именно эти процессы существенно влияют на качество выращенного кристалла. Знание основных параметров всех тепловых процессов, одновременно протекающих при выращивании кристаллов, позволяет сделать выводы о том, какие параметры режима роста яв-ляются решающими, как влиять на них и какие параметры необходимо стабилизировать или изменять в целях оптимизации процесса.
