
Шпора Физика (Оптика)
.pdf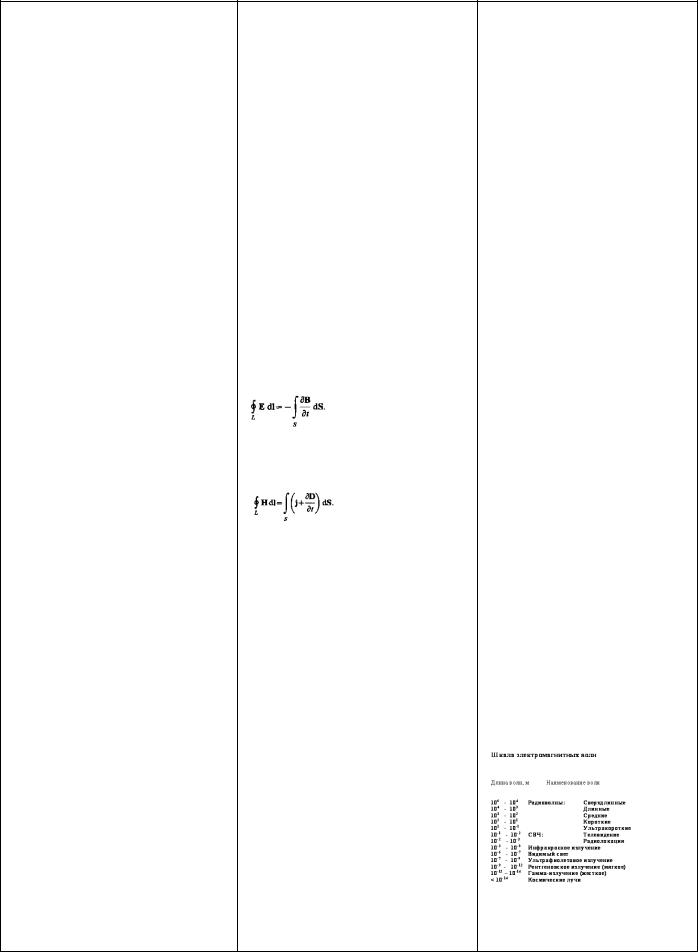
1. Процесс распространения колебаний в сплошной среде называется волновым про-
цессом (или волной). В продольных волнах
частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны. Амплитуда — модуль максимального отклонения тела от положения равновесия. Фаза - состояние волны в данной точке и в данный момент времени. Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах. Фронт волны - геометрическое место точек, имеющих в данный момент одинаковую фазу колебаний.
Монохроматические волны — не-
ограниченные в пространстве волны одной определенной и строго постоянной частоты.
Бегущими волнами называются волны,
которые переносят в пространстве энергию. Стоячие волны — это волны, образующиеся при наложении двух бегущих воли, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией. Гармоническая волна -
линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. Плоская волна — плоскости фаз перпендикулярны направлению распространения волны и параллельны друг другу Сферическая волна — волна, волновые поверхности которой имеют вид концентрических сфер. Световой луч (в геометрической оптике) — линия, вдоль которой переносится световая энергия.
2. Уравнение бегущей волны
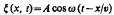 В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет
вид  А = const
А = const
— амплитуда волны, — циклическая частота, 0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t,
[ (t—x/v)+ 0] — фаза плоской волны. Для характеристики волн используется
волновое число  если распространяется в противоположном
если распространяется в противоположном
направлении то вместо "-" пишем "+"
Уравнение сферической волны
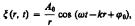 r — расстояние от центра волны до рассматриваемой точки среды
r — расстояние от центра волны до рассматриваемой точки среды
волновое уравнение 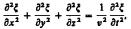 1. Электрическое поле может быть как
1. Электрическое поле может быть как
потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е = ЕQ + ЕB. Так как циркуляция вектора ЕQ равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н
:
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D: 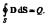 Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула
запишется в виде 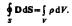 поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.
поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.
4. Теорема Гаусса для поля В : 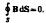 Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
3. Электромагнитные волны —
переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью. Для получения электромагнитных волн непригодны закрытые колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное — внутри катушки индуктивности.
Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представ-
ляющему собой два стрежня, разделенных искровым промежутком. Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора, то в открытом оно заполняет окружающее контур пространство, что существенно повышает интенсивность электромагнитного излучения. Колебания в такой системе поддерживаются за счет источника э.д.с., подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки. Для возбуждения электромагнитных воли вибратор Герца В подключался к индуктору. Когда напряжение на искровом промежутке достигало пробивного значения, возникала искра, закорачивающая обе половины вибратора, и в нем возникали свободные затухающие колебания. Для регистрации электромагнитных воли Герц пользовался вторым вибратором, называемым резонатором Р, имеющим такую же частоту собственных колебаний, что и излучающий вибратор, т. е. настроенным в резонанс с вибратором. Когда электромагнитные волны достигали резонатора, то в его зазоре проскакивала электрическая искра.
Недостатком вибраторов Герца и
Лебедева и массового излучателя Глаголе- вой-Аркадьевой являлось то, что свободные колебания в них быстро затухали и обладали малой мощностью. Поэтому в 20-х годах нашего столетия перешли к генерированию электромагнитных волн с помощью электронных ламп. Ламповые генераторы позволяют получать колебания заданной (практически любой) мощности и синусоидальной формы. Св-ва
электромагнитных волн.
1)они поперечные 2)переносят энергию
3)обладают импульсом 4)Оказывают давление на поверхность
Применение: медицина (рентген), быт (микроволновая печь), передача информации (телевидение, мобильный телефон, радио) и т.д.
4. Закон прямолинейного распространения |
5. Интерференция света - нелинейное сложение |
6. Когерентность - согласованное |
||
света: свет в оптически однородной среде |
интенсивностей двух или нескольких световых |
протекание во времени и пространстве |
||
распространяется прямолинейно. Закон |
волн. Это явление сопровождается |
нескольких колебательных или волновых |
||
независимости световых пучков: эффект, |
чередующимися в пространстве максимумами и |
процессов. Любой немонохроматический |
||
производимый отдельным пучком, не зависит |
минимумами интенсивности. Её распределение |
свет можно представить в виде |
||
от того, действуют ли одновременно остальные |
называется интерференционной картиной. |
совокупности сменяющих друг друга |
||
пучки или они устранены. Закон отражения: |
Условие наблюдения интерференции: |
независимых гармонических цугов (Цуг |
||
отраженный луч лежит в одной плоскости с |
когерентность интерференционных волн. |
волн — это ряд возмущений с |
||
падающим лучом и перпендикуляром, |
условие интерференционного максимума |
перерывами между ними.). Средняя |
||
проведенным к границе раздела двух сред в |
|
|
продолжительность одного цуга ког |
|
точке падения; угол i'1 отражения равен углу i1 |
условие интерференционного минимума |
называется временем когерентности. Если |
||
падения: |
волна распространяется в однородной среде, |
|||
|
|
|||
|
интенсивность |
то фаза колебаний в определенной точке |
||
Закон преломления: луч падающий, луч |
пространства сохраняется только в течение |
|||
2 |
|
|||
|
времени когерентности ког. За это время |
|||
преломленный и перпендикуляр, проведенный к |
результирующей волны (I ~ А |
) |
||
|
|
волна распространяется в вакууме на |
||
границе раздела в точке падения, лежат в одной |
|
(2— 1)=δ |
||
|
расстояние lког =с ког, называемое длиной |
|||
плоскости; отношение синуса угла падения к |
разность фаз, I1,I2 интенсивности источников |
|||
когерентности (или длиной цуга). |
||||
синусу угла преломления есть величина |
||||
Разность фаз колебаний |
|
|||
|
Когерентность колебаний, которые |
|||
постоянная для данных сред: |
|
|||
|
|
|||
|
|
совершаются в одной и той же точке |
||
|
|
|
||
|
|
|
пространства, определяемая степенью |
|
где n21 — относительный показатель |
оптическая разность хода |
|
монохроматичности волн, называется |
|
преломления второй среды относительно |
= L2 – L1 v1=c/n1, v2=c/n2 — соответственно |
временнóй когерентностью. |
||
первой. Индексы в обозначениях углов i1, i'1, i2 |
фазовая скорость первой и второй волны ; /с = |
Пространственная когерентность — |
||
указывают, в какой среде (первой или второй) |
2 /с = 2 /0, где 0 — длина волны в вакууме; |
когерентность колебаний, которые |
||
идет луч. |
Произведение геометрической длины s пути |
совершаются в один и тот же момент |
||
|
световой волны в данной среде на показатель n |
времени в разных точках плоскости, |
||
|
преломления этой среды называется оптической |
перпендикулярной направлению |
||
|
длиной пути L |
|
распространения волны. |
|
|
|
|
Для получения когерентных световых |
|
|
|
|
волн с помощью обычных (нелазерных) |
|
|
|
|
источников применяют метод разделения |
|
|
|
|
света от одного источника на две или |
|
|
|
|
нескольких систем волн (световых пучков). |
|
|
|
|
В каждой из них представлено излучение |
|
|
|
|
одних и тех же атомов источника, так что |
|
|
|
|
эти волны когерентны между собой и |
|
|
|
|
интерферируют при наложении. |
|
|
|
|
Разделение света на когерентные пучки |
|
|
|
|
можно осуществить с помощью экранов и |
|
|
|
|
щелей, зеркал и преломляющих тел. (Метод |
|
|
|
|
Юнга, Бипризма Френеля и т.д.) |
|
7. Полосы равного наклона (интерференция |
8. Дифракция света – явление, которое |
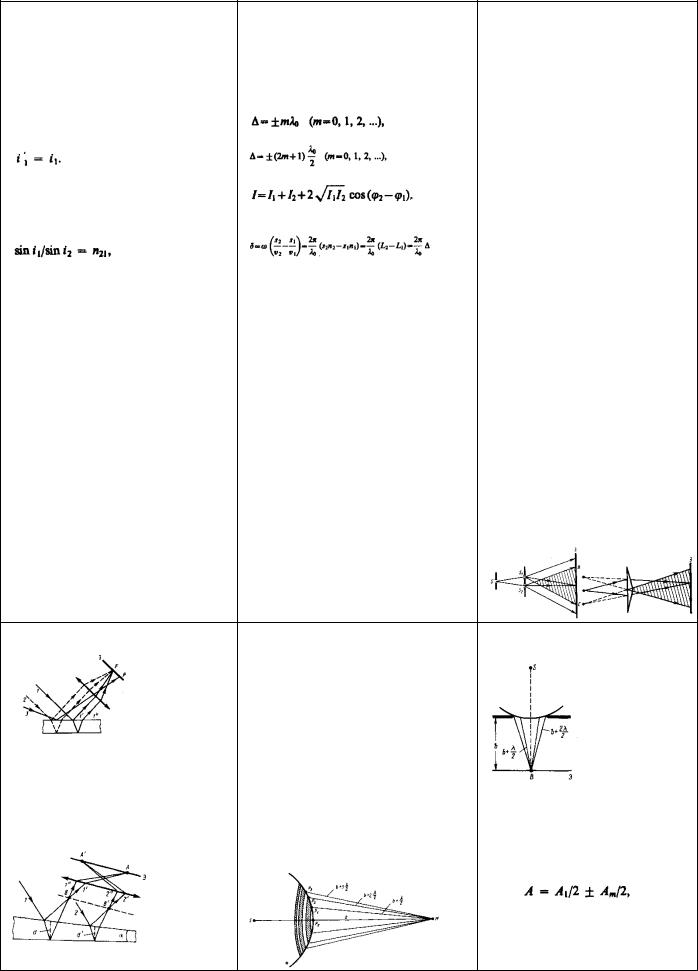
9. Дифракция на круглом отверстии. |
от плоскопараллельной пластинки). |
наблюдается при распространении света сквозь |
Сферическая волна, распространяющаяся из |
|
препятствие и состоит в том, что свет |
точечного |
|
препятствие огибает, т.е. нарушается |
источника S, |
|
прямолинейность распространения света. |
встречает на своем |
|
Условие наблюдения: размер препятствия |
пути экран с |
|
должен быть соизмерим с длиной волны. |
круглым |
|
Принцип Гюйгенса-Френеля 1. Световая волна |
отверстием. |
|
возбуждаемая каким-либо источником может |
Дифракционную |
|
быть представлена как результат суперпозиции, |
картину наблюдаем |
Интерференционные полосы, возникающие в |
когерентных вторичных волн. 2. Вторичные |
на экране Э в точке |
результате наложения лучей, падающих на |
волны являются сферическими, их огибающая – |
В, лежащей на |
плоскопараллельную пластинку под |
новое положение волнового фронта 3. Если |
линии, |
одинаковыми углами, называются полосами |
между источником и экраном помещено |
соединяющей S с центром отверстия. Экран |
равного наклона. |
препятствие, то его влияние учитывается след. |
параллелен плоскости отверстия и |
|
образом: В области непрозрачн. частей |
находится от него на расстоянии b. Разобьем |
Полосы равной толщины (интерференция от |
препятствия амплитуды вторичных источников = |
открытую часть волновой поверхности Ф на |
пластинки переменной толщины). |
0, а на открытых участках амплитуды такие же |
зоны Френеля. Вид дифракционной картины |
|
как при отсутствии препятствия. |
зависит от числа зон Френеля, открываемых |
|
Метод зон Френеля |
отверстием. Амплитуда результирующего |
|
|
колебания, возбуждаемого в точке В всеми |
|
|
зонами, |
|
|
где знак плюс соответствует нечетным m и |
|
|
минус — четным т. Когда отверстие |
|
|
открывает нечетное число зон Френеля, то |
|
|
амплитуда (интенсивность) в точке В будет |
Интерференционные полосы, возникающие в |
|
больше, чем при свободном |

результате интерференции от мест одинаковой |
Френель разбил волновую поверхность Ф на |
распространении волны; если четное, то |
||||||
толщины, называются полосами равной |
кольцевые зоны такого размера, чтобы |
|
амплитуда (интенсивность) будет равна |
|||||
толщины. |
расстояния от краев зоны до М отличались на |
нулю. Если отверстие открывает одну зону |
||||||
Кольца Ньютона. |
/2, т. е. Р1М – Р0М = Р2М – Р1М = Р3М – Р2М = |
Френеля, то в точке В амплитуда А=А1, т. е. |
||||||
Кольца Ньютона, |
... = /2 |
|
|
|
|
|
вдвое больше, чем в отсутствие |
|
являющиеся |
Подобное разбиение фронта волны на зоны |
непрозрачного экрана с отверстием. |
||||||
классическим |
можно выполнить, проведя с центром в точке М |
Интенсивность света больше соответственно |
||||||
примером полос |
|
|
|
|
|
в четыре раза. Если отверстие открывает две |
||
равной толщины, |
|
|
зоны Френеля, то их действия в точке В |
|||||
сферы радиусами b + |
|
, b + 2 , b + 3 |
, ... . |
|||||
наблюдаются при |
|
практически уничтожат друг друга из-за |
||||||
|
2 |
|
2 |
|
2 |
|||
отражении света от |
|
|
|
интерференции. Таким образом, |
||||
Так как колебания от соседних зон проходят до |
||||||||
воздушного зазора, |
дифракционная картина от круглого |
|||||||
точки М расстояния, отличающиеся на /2, то в |
||||||||
образованного |
отверстия вблизи точки В будет иметь вид |
|||||||
точку М они приходят в противоположной фазе |
||||||||
плоскопараллельной |
чередующихся темных и светлых колец с |
|||||||
и при наложении эти колебания будут взаимно |
||||||||
пластинкой и |
центрами в точке В (если т четное, то в |
|||||||
ослаблять друг друга. Поэтому амплитуда |
|
|||||||
соприкасающейся с ней плосковыпуклой |
|
центре будет темное кольцо, если m |
||||||
результирующего светового колебания в точке М |
||||||||
линзой с большим радиусом кривизны. |
нечетное — то светлое кольцо), причем |
|||||||
|
|
|
|
|
|
|||
Параллельный пучок света падает нормально на |
|
|
|
|
|
|
интенсивность в максимумах убывает с |
|
плоскую поверхность линзы и частично |
где А1, А2, ... — амплитуды колебаний, |
|
расстоянием от центра картины. |
|||||
отражается от верхней и нижней поверхностей |
|
Дифракция на диске. Сферическая волна, |
||||||
возбуждаемых 1-й, 2-й, ..., т-й зонами. |
|
|||||||
воздушного зазора между линзой и пластинкой. |
|
распространяющаяся от точечного |
||||||
|
|
|
|
|
|
|||
При наложении отраженных лучей возникают |
|
|
|
|
|
|
источника S, встречает на своем пути диск. |
|
полосы равной толщины, при нормальном |
|
|
|
|
|
|
Дифракционную картину наблюдаем на |
|
падения света имеющие вид концентрических |
|
|
|
|
|
|
экране Э в точке В, лежащей на линии, |
|
окружностей. |
|
|
|
|
|
|
соединяющей S с центром диска (рис. 260). |
|
Применения интерференции света Явление |
|
|
|
|
|
|
В данном случае закрытый диском участок |
|
интерференции применяется для улучшения |
|
|
|
|
|
|
волнового фронта надо исключить из |
|
качества оптических приборов (просветление |
|
|
высота сферич. |
рассмотрения и зоны Френеля строить |
||||
оптики) и получения высокоотражающих |
|
|
начиная с краев диска. Пусть диск закрывает |
|||||
|
|
|
|
|
|
|||
покрытий. |
сегмента |
|
|
|
|
|
m первых зон Френеля. Тогда амплитуда |
|
|
|
|
|
|
|
результирующего колебания в точке В равна |
||
|
|
|
|
|
|
|
||
|
радиус внешн. границы m-ой зоны |
|
или |
|||||
|
площадь сферич. сегмента и площадь m-ой зоны |
|||||||
|
|
|||||||
|
|
|
|
|
|
|
так как выражения, |
|
|
Площади зон равны. |
|
A= А1/2 |
|
стоящие в скобках, |
|||
|
|
|
|
|
|
|
равны нулю. |
|
|
|
|
|
|
|
|
Следовательно, в |
|
|
|
|
|
|
|
|
точке В всегда |
|
|
|
|
|
|
|
|
наблюдается |
|
|
|
|
|
|
|
|
интерференционный |
|
|
|
|
|
|
|
|
максимум (светлое |
|
|
|
|
|
|
|
|
пятно), |
|
|
|
|
|
|
|
|
соответствующий |
|
|
|
|
|
|
|
|
половине действия первой открытой зоны |
|
|
|
|
|
|
|
|
Френеля. Центральный максимум окружен |
|
|
|
|
|
|
|
|
концентрическими с ним темными и |
|
|
|
|
|
|
|
|
светлыми кольцами, а интенсивность в мак- |
|
|
|
|
|
|
|
|
симумах убывает с расстоянием от центра |
|
|
|
|
|
|
|
|
картины. |
|
10. Дифракция Фраунгофер на |
11. Основные характеристики спектральных |
12. Поляризация света; естественный, |
||||||
прямоугольном отверстии |
приборов: дисперсия (линейная и угловая), |
частично поляризованный и |
||||||
надо поставить |
разрешающая способность оптических |
|
поляризованный свет; состояния |
|||||
линзу за щелью |
приборов, критерий Рэлея. |
|
|
|
поляризации. |
|||
в фок. пл-ти |
|
|
|
|
|
|
|
|
линзы |
Спектральными называются оптические |
|
Свет со всевозможными равновероятными |
|||||
помещаем |
приборы, в которых осуществляется разложение |
ориентациями вектора Е (и, следовательно, |
||||||
экран; φ – угол |
электромагнитного излучения оптического |
Н) называется естественным. |
||||||
дифракции. |
диапазона на монохроматические составляющие. |
Свет, в котором направления колебаний |
||||||
Условие max |
Линейная дисперсия |
|
|
|
|
|
светового вектора каким-то образом |
|
число зон |
|
|
|
|
|
|
упорядочены, называется поляризованным. |
|
Френеля |
Одной из самых важных характеристик |
|
Частично поляризованный свет - сумма |
|||||
нечетное |
спектрального прибора является линейная |
естественного и поляризованного света. |
||||||
|
дисперсия, которая показывает, как быстро |
Плоско (линейно) поляризованный свет - |
||||||
|
изменяется расстояние между спектральными |
свет, в котором вектор E колеблется только |
||||||
|
линиями в фокальной плоскости в зависимости |
в одном направлении, перпендикулярно |
||||||
|
от длины волны . |
|
|
|
|
|
лучу. |
|
|
Разрешающая способность прибора |
|
|
|||||
|
характеризует возможность раздельной |
|
|
|||||
. |
регистрации соседних спектральных интервалов. |
|
||||||
Условие min число зон Френеля чётное |
Количественно разрешающая способность |
|
||||||
(полная темнота) |
определяется соотношением: |
|
|
|
|
|||
R=λ/δλ где величина δλ называется пределом |
|
|||||||
Распределение интенсивности При увеличении |
|
|||||||
разрешения прибора и определяется шириной |
|
|||||||
размеров щели, интенсивность центр. max |
|
|||||||
инструментального контура линии. |
Согласно |
|
||||||
увеличивается и увеличивается кол-во max |
|
|||||||
критерию Рэлея, изображения двух |
|
|
||||||
|
|
|
||||||
|
близлежащих одинаковых точечных источников |
|
||||||

Дифракция Фраунгофера на дифракционной |
или двух близлежащих спектральных линий с |
|
||
решётке |
|
равными интенсивностями и одинаковыми |
|
|
|
|
симметричными контурами разрешимы |
|
|
|
|
(разделены для восприятия), если центральный |
|
|
|
|
максимум дифракционной картины от одного |
|
|
|
|
источника (линии) совпадает с первым |
|
|
|
|
минимумом дифракционной картины от другого. |
|
|
|
|
При выполнении критерия Рэлея интенсивность |
|
|
|
|
«провала» между максимумами составляет 80% |
|
|
|
|
интенсивности в максимуме, что является |
|
|
|
|
достаточным для разрешения линий 1 и 2. Если |
|
|
|
|
критерий Рэлея нарушен, то наблюдается одна |
|
|
Усл. гл-х min bsin =k (k=1,2…) Усл. гл-х |
линия. |
|
||
max dsin =m (m=0,1,2…) |
|
|
|
|
Число штрихов ДР = N Усл. побочных min |
|
|
||
где m' может принимать все целочисленные |
|
|
||
значения, кроме 0, N, 2N, .... |
|
|
|
|
Чем больше N тем больше побочных min набл. |
|
|
||
между соседними главными max и max-мы |
|
|
||
более острые, т.е. имеют большую |
|
|
||
интенсивность |
|
|
|
|
13. Естественный свет можно преобразовать в |
14. Если угол падения света на границу раздела |
15. Двойное лучепреломление. |
||
плоскополяризованный, используя так |
двух диэлектриков (например, на поверхность |
Поляризационные устройства. |
||
называемые поляризаторы, пропускающие |
стеклянной пластинки) отличен от нуля, |
Интерференция поляризованного света. |
||
колебания только определенного направления |
отраженный и преломленный лучи оказывают |
|
||
(например, пропускающие колебания, |
частично |
Все прозрачные кристаллы (кроме |
||
параллельные главной плоскости поляризатора, |
поляризованными. |
кристаллов кубической системы, которые |
||
и полностью задерживающие колебания, |
Причем, при |
оптически изотропны) обладают |
||
перпендикулярные этой плоскости). |
отражении от |
способностью двойного лучепреломления, т. |
||
Закон Малюса — зависимость интенсивности |
проводящей |
е. раздваивания каждого падающего на них |
||
линейно-поляризованного света после его |
поверхности |
светового пучка. когда первичный пучок |
||
прохождения через поляризатор от |
(например, от |
падает на кристалл нормально, |
||
угла φ между |
|
поверхности |
преломленный пучок разделяется на два, |
|
плоскостями поляризации падающего света и |
металла) получается |
причем один из них является продолжением |
||
поляризатора. |
I — |
эллиптически- |
первичного, а второй отклоняется (рис. 278). |
|
поляризованный свет. В отраженном луче |
Второй из этих лучей получил название |
|||
интенсивность света, прошедшего через |
||||
преобладают колебания, перпендикулярные к |
необыкновенного (e), а первый — |
|||
анлизатор, I0 – интенсивность света |
||||
плоскости падения (на рис. 6.2 эти колебания |
обыкновенного (о). |
|||
прошедшего через поляризатор, α-угол между |
||||
обозначены точками), в преломленном луче |
|
|||
главными осями анализатора и поляризатора |
|
|||
колебания, параллельные плоскости падения (на |
|
|||
Степень поляризации |
|
|
||
|
рисунке они изображены двусторон-ними |
|
||
Если пропустить частично поляризованный свет |
|
|||
стрелками). Степень поляриза-ции зависит от |
|
|||
через поляризатор, то при вращении прибора |
|
|||
угла падения. |
|
|||
вокруг направления луча интенсивность |
|
|||
Д. Брюстер (1781—1868) установил закон, |
|
|||
прошедшего света будет изменяться в пределах |
ПОЛЯРИЗАЦИОННЫЕ ПРИБОРЫ |
|||
согласно которому при угле падения iB (угол |
||||
от Imax до Imin, причем переход от одного из этих |
оптич. приборы для обнаружения, анализа, |
|||
Брюстера), определяемого соотношением |
||||
значений к другому будет совершаться при |
получения и преобразования |
|||
|
||||
повороте на угол, равный π/2 (за один полный |
|
поляризованного оптического излучения |
||
поворот два раза будет достигаться |
(n21 — показатель преломления второй среды |
(света), а также для разл. исследований и |
||
максимальное и два раза минимальное значение |
относительно первой), отраженный луч |
измерений, основанных на явлении |
||
интенсивности). Выражение |
|
является плоскополяризованным (содержит |
поляризации света |
|
|
|
только колебания, перпендикулярные плоскости |
. Для получения полностью или частично |
|
|
|
падения). Преломленный же луч при угле падения |
поляризованного света используется одно из |
|
|
|
iB поляризуется максимально, но не полностью. |
трёх физ. явлений: |
|
называется степенью поляризации. Для |
Если свет падает на границу раздела под углом |
1) поляризация при отражении света или |
||
плоскополяризованного света Imin=0 и Р=1; для |
Брюстера, то отраженный и преломленный лучи |
преломлении света на границе раздела двух |
||
естественного света Imax=Imin и P=0 |
взаимно перпендикулярны (tgiB = siniB/cosiB, |
прозрачных сред; 2) линейный дихроизм; |
||
|
|
n21=siniB/sini2 (i2 — угол преломления), откуда |
3) двойное лучепреломление. |
|
|
|
cosiB=sini2). Следовательно, iB + i2 = /2, но i’B = |
ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ |
|
|
|
iB (закон отражения), поэтому i’B + i2 = /2. |
ЛУЧЕЙ |
|
|
|
|
света, явление, возникающее при сложении |
|
|
|
|
когерентных поляризованных световых |
|
|
|
|
колебаний |
|
|
|
|
Наибольший контраст интерференционной |
|
|
|
|
картины наблюдается при сложении |
|
|
|
|
колебаний одного вида поляризации |
|
|
|
|
(линейных, круговых, эллиптических) с |
|
|
|
|
совпадающими азимутами. Ортогональные |
|
|
|
|
колебания не интерферируют. Так, при |
|
|
|
|
сложении двух линейно поляризованных |
|
|
|
|
взаимно перпендикулярных колебаний в |
|
|
|
|
общем случае возникает эллиптически |
|
|
|
|
поляризованное колебание, интенсивность |
|
|
|
|
к-рого равна сумме интенсивностей |
|
|
|
|
исходных колебаний. |
|
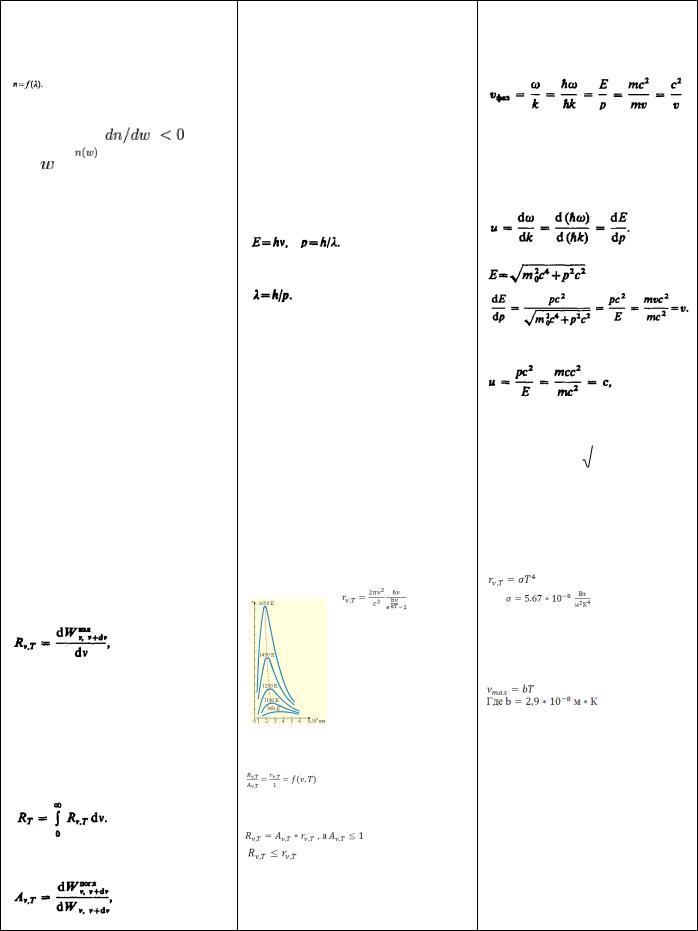
16. Дисперсией света называется зависимость |
17. Корпускулярно-волновой дуализм — |
18. Гипотеза де Бройля. Свойства волн де |
||
показателя преломления n вещества от частоты |
принцип, согласно которому любой объект |
Бройля. |
||
(длины волны ) света или зависимость |
может проявлять как волновые, так |
Рассмотрим свободно движущуюся со |
||
фазовой скорости v световых волн (см. § 154) от |
и корпускулярные свойства |
скоростью v частицу массой т. Вычислим |
||
его частоты . Дисперсия света представляется |
Такие явления, как интерференция и дифракция |
для нее фазовую и групповую скорости волн |
||
в виде зависимости |
|
света, убедительно свидетельствуют о волновой |
да Бройля. Фазовая скорость |
|
|
|
природе света. В то же время закономерности |
|
|
Аномальная дисперсия — вид дисперсии |
равновесного теплового излучения, фотоэффекта |
|
||
и эффекта Комптона можно успешно |
|
|||
света, при которой показатель преломления |
|
|||
истолковать с классической точки зрения только |
|
|||
среды уменьшается с увеличением частоты |
|
|||
на основе представлений о свете, как о потоке |
(E=ћ и p=ћk, где k=2 / —волновое |
|||
|
|
|||
световых колебаний. |
дискретных фотонов. Однако волновой и |
число). Так как c>v, то фазовая скорость |
||
(dn/d >0), где |
— показатель преломления |
корпускулярный способы описания света не |
волн де Бройля больше скорости света в |
|
среды, — циклическая частота волны. |
противоречат, а взаимно дополняют друг друга, |
вакууме (фазовая скорость волн может быть |
||
Наблюдается в областях спектра, |
так как свет одновременно обладает и |
как меньше, так и больше с в отличие от |
||
соответствующих полосам интенсивного |
волновыми и корпускулярными свойствами. |
групповой скорости волн (см. § 155)). |
||
поглощения света в среде. |
Количественные соотношения, связывающие |
Групповая скорость, согласно (155.1), |
||
Нормальная дисперсия - когда dn/dω>0 |
корпускулярные и волновые свойства частиц, |
|
||
(dn/d <0) n увеличивается с ростом ω(убывает |
такие же, как для фотонов: |
|
||
с ростом ). Наблюдается у прозрачных для |
|
|
||
света веществ. |
|
Давление излучения |
Для свободной частицы |
|
Классическая электронная теория дисперсии |
- давление, оказываемое эл.-магнитным |
|
||
Последовательное описание взаимодействия |
излучением на тела, взаимодействующие с ним. |
и |
||
света с веществом возможно только в |
|
|||
|
|
|||
рамках квантовой теории. Однако, во многих |
|
|
||
случаях можно ограничиться описанием в |
|
|
||
рамках волновой (электромагнитной) теории |
|
Следовательно, групповая скорость волн де |
||
излучения и классической электронной теории , |
|
|||
|
Бройля равна скорости частицы. |
|||
согласно которой каждую молекулу среды |
|
|||
|
Групповая скорость фотона |
|||
можно рассматривать как систему зарядов, |
|
|||
|
|
|||
имеющих возможность совершать |
|
|
||
гармонические колебания - как |
|
т. е. равна |
||
систему осцилляторов с различными |
|
|||
|
скорости самого фотона. |
|||
собственными частотами и коэффициентами |
|
|||
|
Волны да Бройля испытывают дисперсию. |
|||
затухания. Движение этих осцилляторов можно |
|
|||
|
Действительно, подставив в выражение |
|||
рассматривать на основе законов Ньютона. |
|
|||
|
|
|||
|
|
|
|
|
m2 c4 |
p2 c2 |
|
|
|
|
|
vфаз=E/p формулу Е= |
0 |
, |
|
|
|
|
|
|
|||
|
|
|
|
увидим, что скорость волн де Бройля |
|||
|
|
|
|
зависит от длины волны. |
|
|
|
19. Тепловое излучение. Характеристики |
20. Спектр излучения абсолютно чёрного |
21. Законы Стефана-Больцмана и |
|||||
теплового излучения |
тела. Закон Кирхгофа. |
смещения Вина. |
|
|
|
||
Тепловое излучение – электромагнитное |
На основе гипотезы о прерывистом характере |
Закон Стефана-Больцмана. Интегральная |
|||||
излучение, испускаемое нагретыми телами. |
процессов излучения и поглощения телами |
излучательная способность абсолютно |
|||||
Количественной характеристикой теплового |
электромагнитного излучения Планк получил |
черного тела пропорциональна его |
|||||
излучения служит спектральная плотность |
формулу для спектральной светимости |
температуре в четвертой степени |
|||||
энергетической светимости (излучательности) |
абсолютно черного тела. |
|
|
|
|
||
тела — мощность излучения с единицы |
|
|
|
|
|
||
площади поверхности тела в интервале частот |
|
Где |
постоянная |
||||
единичной ширины: |
|
Стефана-Больцмана. |
|
|
|
||
|
|
|
Спектральное |
Закон смещения Вина. Частота, |
|||
|
|
|
распределение r (λ, T) |
соответствующая максимуму излучательной |
|||
|
|
|
излучения черного тела при |
способности абсолютно черного тела, с |
|||
|
|
|
различных температурах |
ростом температуры смещается в область |
|||
|
изл |
|
Отношение излучательной и |
более высоких частот. |
|
|
|
где d |
W , d |
— энергия электромагнитного |
поглощательной |
|
|
|
|
|
|
|
|
|
|||
|
способностей любого тела |
|
|
|
|
||
излучения, испускаемого за единицу времени |
|
-постоянная Вина |
|||||
(мощность излучения) с единицы площади |
не зависит от природы этого |
|
|
|
|
||
тела, оно является для всех тел одной и той же |
|
|
|
|
|||
поверхности тела в интервале частот от до |
|
|
|
|
|||
+d . можно вычислить интегральную |
функцией частоты и температуры, равной |
|
|
|
|
||
излучательной способности абсолютно черного |
|
|
|
|
|||
энергетическую светимость (интегральную |
|
|
|
|
|||
тела. |
|
|
|
|
|||
излучательность) (ее называют просто |
|
|
|
|
|||
|
|
|
|
|
|||
энергетической светимостью тела), |
Закон Кирхгофа |
|
|
|
|
||
просуммировав по всем частотам: |
|
|
|
|
|||
Из закона следует что максимальной |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
излучательной способностью при данной |
|
|
|
|
|
|
|
температуре обладает обладает черное тело, т.к , |
|
|
|
|
|
Способность тел поглощать |
.Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
||
падающее на них излучение характеризуется |
. |
|
|
|
|
||
спектральной поглощательной способностью |
|
|
|
|
|
||

22. Внешний фотоэффект (вольт-амперная |
23. Эффект Комптона. |
24. Соотношения неопределённостей |
|
характеристика, законы фотоэффекта, |
Наиболее полно корпускулярные свойства света |
Гейзенберга. |
|
уравнение Эйнштейна). |
проявляются в эффекте Комптона. |
В. Гейзенберг, учитывая волновые свойства |
|
Внешним фотоэлектрическим эффектом |
Американский физик А. Комптон (1892—1962), |
микрочастиц и связанные с волновыми |
|
(фотоэффектом) называется испускание |
исследуя в 1923 г. рассеяние мо- |
свойствами ограничения в их поведении, |
|
электронов веществом под действием |
нохроматического рентгеновского излучения |
пришел в 1927 г. к выводу, что объект |
|
электромагнитного излучения. Внешний |
веществами с легкими атомами (парафин, бор), |
микромира невозможно одновременно с |
|
фотоэффект наблюдается в твердых телах |
обнаружил, что в составе рассеянного излучения |
любой наперед заданной точностью харак- |
|
(металлах, полупроводниках, диэлектриках), а |
наряду с излучением первоначальной длины |
теризовать и координатой и импульсом. |
|
также в газах на отдельных атомах и молекулах |
волны наблюдается также более длинноволновое |
Согласно соотношению неопределенностей |
|
(фотоионизация). Фотоэффект обнаружен (1887 |
излучение. Опыты показали, что разность = '– |
Гейзенберга, микрочастица (микрообъект) |
|
г.) Г. Герцем, наблюдавшим усиление процесса |
не зависит от длины волны падающего |
не может иметь одновременно и определен- |
|
разряда при облучении искрового промежутка |
излучения и природы рассеивающего вещества, а |
ную координату (х, у, z), и определенную |
|
ультрафиолетовым излучением. |
определяется только углом рассеяния : |
соответствующую проекцию импульса (рх, |
|
вольт-амперная характеристика |
|
pу, pz), причем неопределенности этих |
|
фотоэффекта — зависимость фототока I, |
где ' — длина |
величин удовлетворяют условиям |
|
образуемого потоком электронов, испускаемых |
волны рассеянного излучения, С — |
|
|
катодом под действием света, от напряжения U |
комптоновская длина волны (при рассеянии |
т. е. произведение неопределенностей |
|
между электродами. По мере увеличения U |
|||
фотона на электроне С= 2,426 пм). |
координаты и соответствующей ей проекции |
||
фототок постепенно возрастает, т. е. все |
|||
|
импульса не может быть меньше величины |
||
большее число фотоэлектронов достигает |
|
||
Эффектом Комптона называется упругое |
порядка h. |
||
анода. Максимальное значение тока Iнас — |
|||
рассеяние коротковолнового электромагнитного |
|
||
фототок насыщения — определяется таким |
|
||
излучения (рентгеновского и -излучений) на |
|
||
значением U, при котором все электроны, |
|
||
свободных (или слабосвязанных) электронах |
|
||
испускаемые катодом, достигают анода: |
|
||
вещества, сопровождающееся увеличением |
|
||
|
|
||
|
длины волны. |
|
|
где n — число электронов, испускаемых |
|
|
|
катодом в 1 с. |
|
|
|
Из вольт-амперной характеристики следует, что |
|
|
|
при U=0 фототок не исчезает. Для того чтобы |
|
|
|
фототок стал равным нулю, необходимо |
|
|
|
приложить задерживающее напряжение U0. |
|
|
|
Следовательно, |
|
|
|
три закона внешнего фотоэффекта. |
|
|
|
I. Закон Столетова: при фиксированной |
|
|
|
частоте падающего света число фотоэлект- |
|
|
|
ронов, вырываемых из катода в единицу |
|
|
|
времени, пропорционально интенсивности света |
|
|
|
(сила фототока насыщения пропорциональна |
|
|
|
энергетической освещенности Ее катода). |
|
|
|
II. Максимальная начальная скорость |
|
|
|
(максимальная начальная кинетическая энер- |
|
|
|
гия) фотоэлектронов не зависит от |
|
|
|
интенсивности падающего света, а определяется |
|
|
|
только его частотой . |
|
|
|
III. Для каждого вещества существует красная |
|
|
|
граница фотоэффекта, т. е. минимальная частота |
|
|
|
0 света (зависящая от химической природы |
|
|
|
вещества и состояния его поверхности), ниже |
|
|
|
которой фотоэффект невозможен. |
|
|
|
уравнение Эйнштейна для внешнего |
|
|
|
фотоэффекта. |
|
|
|
Энергия падающего фотона расходуется на |
|
|
|
совершение электроном работы выхода А из |
|
|
|
металла (см. § 104) и на сообщение |
|
|
|
вылетевшему фотоэлектрону кинетической |
|
|
|
энергии mv2max/2. По закону сохранения |
|
|
|
энергии, |
|
|
|
|
|
|
|
25. Зонная теория твердых тел. |
26. Атом водорода. Модели Томсона и |
27. Постулаты Бора. |
|
Если в твердом теле имеется зона, лишь |
Резерфорда. |
Первый постулат Бора (постулат |
|
частично заполненная электронами, то это тело |
Первая попытка создания на основе |
стационарных состояний): в атоме |
|
всегда будет проводником электрического тока. |
накопленных экспериментальных данных |
существуют стационарные (не |
|
Именно это свойственно металлам. |
модели атома принадлежит Дж. Дж. Томсону |
изменяющиеся со временем) состояния, в |
|
Твердое тело является проводником |
(1903). Согласно этой модели, атом представляет |
которых он не излучает энергии. |
|
электрического тока и в том случае, когда |
собой непрерывно заряженный положительным |
Стационарным состояниям атома |
|
валентная зона перекрывается свободной зоной, |
зарядом шар радиусом порядка 10–10 м, внутри |
соответствуют стационарные орбиты, по |
|
что в конечном счете приводит к не полностью |
которого около своих положений равновесия |
которым движутся электроны. Движение |
|
заполненной. Это имеет место для |
колеблются электроны; суммарный |
электронов по стационарным орбитам не |
|
щелочноземельных элементов, образующих II |
отрицательный заряд электронов равен |
сопровождается излучением |
|
группу таблицы Менделеева (Be, Mg, Ca, Zn, |
положительному заряду шара, поэтому атом в |
электромагнитных волн. |
|
...). В данном случае образуется так называемая |
целом нейтрален. Через несколько лет было |
В стационарном состоянии атома электрон, |
|
«гибридная» зона, которая заполняется |
доказано, что представление о непрерывно |
двигаясь по круговой орбите, должен иметь |
|
валентными электронами лишь частично. |
распределенном внутри атома положительном |
дискретные квантованные значения момента |
|
Следовательно, в данном случае металлические |
заряде ошибочно.На основании своих |
импульса, удовлетворяющие условию |

свойства щелочноземельных элементов |
исследований Резерфорд в 1911 г. предложил |
|
||
обусловлены перекрытием валентной и |
ядерную (планетарную) модель атома. |
|
||
свободной зон. |
Согласно этой модели, вокруг положительного |
где те — масса электрона, v — его скорость |
||
Твердые тела, у которых энергетический спектр |
ядра, имеющего заряд Zе (Z — порядковый |
|||
по n-й орбите радиуса rn, ћ = h/(2 ). |
||||
электронных состояний состоит только из |
номер элемента в системе Менделеева, е — |
|||
Втором постулат Бора (правило частот): |
||||
валентной зоны и зоны проводимости, являются |
элементарный заряд), размер 10–15—10–14 м и |
|||
диэлектриками или полупроводниками в |
массу, практически равную массе атома, в |
при переходе электрона с одной стационар- |
||
ной орбиты на другую излучается |
||||
зависимости от ширины запрещенной зоны Е. |
области с линейными размерами порядка 10–10 м |
|||
Различие между металлами и диэлектриками с |
по замкнутым орбитам движутся электроны, |
(поглощается) один фотон с энергией |
||
|
||||
точки зрения зонной теории состоит в том, что |
образуя электронную оболочку атома. Так как |
|
||
при 0 К в зоне проводимости металлов имеются |
атомы нейтральны, то заряд ядра равен |
|
равной разности энергий соответствующих |
|
электроны, а в зоне проводимости диэлектриков |
суммарному заряду электронов, т. е. вокруг ядра |
|||
стационарных состояний (Еn и Em — соот- |
||||
они отсутствуют. Различие же между |
должно вращаться Z электронов. |
|
||
|
ветственно энергии стационарных |
|||
диэлектриками и полупроводниками |
|
|
||
|
|
состояний атома до и после излучения |
||
определяется шириной запрещенных зон: для |
|
|
||
|
|
(поглощения)). При Еm<Еn происходит |
||
диэлектриков она довольно широка (например, |
|
|
||
для NaCl Е=6 эВ), для полупроводников — |
|
|
излучение фотона (переход атома из |
|
|
|
состояния с большей энергией в состояние с |
||
достаточно узка (например, для германия |
|
|
||
|
|
меньшей энергией, т. е. переход электрона с |
||
Е=0,72 эВ). При температурах, близких к 0 К, |
|
|
||
|
|
более удаленной от ядра орбиты на более |
||
полупроводники ведут себя как диэлектрики, |
|
|
||
|
|
близлежащую), при Еm>Еn — его |
||
так как переброса электронов в зону |
|
|
||
|
|
поглощение (переход атома в состояние с |
||
проводимости не происходит. С повышением |
|
|
||
|
|
большей энергией, т. е. переход электрона |
||
температуры у полупроводников растет число |
|
|
||
|
|
на более удаленную от ядра орбиту). Набор |
||
электронов, которые вследствие теплового |
|
|
||
|
|
возможных дискретных частот = (En— |
||
возбуждения переходят в зону проводимости, т. |
|
|
||
|
|
Em)/h квантовых переходов и определяет |
||
е. электрическая проводимость проводников в |
|
|
||
|
|
линейчатый спектр атома. |
||
этом случае увеличивается. |
|
|
||
|
|
|
||
28. Спектр излучения атома водорода. |
29. Квантовые числа. В квантовой механике |
30. Спонтанное и вынужденное излучение |
||
Опыты Франка и Герца. |
доказывается, что уравнению Шредингера |
фотонов. Поглощение фотонов. |
||
Изучая методом задерживающего потенциала |
удовлетворяют собственные функции |
|
Процесс испускания фотона возбужденным |
|
столкновения электронов с атомами газов |
nlm (r, , ) , определяемые тремя |
|
атомом без каких-либо внешних воз- |
|
(1913), Д. Франк и Г. Герц экспериментально |
|
действий называется спонтанным (или |
||
l |
|
|||
доказали дискретность значений энергии |
квантовыми числами: главным п, орбитальным l |
самопроизвольным) излучением. |
||
атомов. Принципиальная схема их установки |
и магнитным тl. |
|
Если на атом, находящийся в возбужденном |
|
приведена на рисунке. Вакуумная трубка, |
Главное квантовое число n, согласно (223.3), |
состоянии, действует внешнее излучение с |
||
заполненная парами ртути (давление |
определяет энергетические уровни электрона в |
частотой, удовлетворяющей условию |
||
приблизительно равно 13 Па), содержала катод |
атоме и может принимать любые целочисленные |
hv=E2–E1, то возникает вынужденный |
||
(К), две сетки (C1 и С2) и анод (А). Электроны, |
значения начиная с единицы: n=1,2,3, … |
|
(индуцированный) переход в основное |
|
эмиттируемые катодом, ускорялись разностью |
Из решения уравнения Шредингера вытекает, |
состояние с излучением фотона той же |
||
потенциалов, приложенной между катодом и |
что момент импульса (механический |
|
энергии hv=E2–E1 . При подобном переходе |
|
сеткой C1. Между сеткой С2 и анодом приложен |
орбитальный момент) электрона квантуется, т. |
происходит излучение атомом фотона, |
||
небольшой (примерно 0,5 В) задерживающий |
е. не может быть произвольным, а принимает |
дополнительно к тому фотону, под |
||
|
дискретные значения, определяемые формулой |
действием которого произошел переход. |
||
|
|
|
Возникающее в результате таких переходов |
|
потенциал. |
где l - орбитальное |
|
излучение называется вынужденным |
|
Из опыта следует (см. рис) что при увеличении |
квантовое число, которое при заданном n |
(индуцированным) излучением. |
||
ускоряющего потенциала вплоть до 4,86 В |
принимает значения l=0,1,…,(n-1) |
т. е. |
Однако наряду с вынужденным излучением |
|
анодный ток возрастает монотонно, его |
всего n значений, и определяет момент импульса |
возможен и конкурирующий процесс — |
||
значение проходит через максимум (4,86 В), |
электрона в атоме. |
|
поглощение. |
|
затем резко уменьшается и возрастает вновь. |
Из решения уравнений Шредингера следует |
|
||
Дальнейшие максимумы наблюдаются при |
также, что вектор Ll момента импульса |
|
|
|
2 4,86 и 3 4,86 В. |
электрона может иметь лишь такие ориентации в |
|
||
|
пространстве, при которых его проекция Llx на |
|
||
Таким образом, |
направление z внешнего магнитного поля |
|
||
опыты Франка и |
принимает квантованные значения, кратные ћ: |
|
||
Герца показали, что |
где тl — магнитное квантовое |
|
||
электроны при |
|
|||
число, которое при заданном l может принимать |
|
|||
столкновении с |
|
|||
|
|
|
||
атомами ртути |
значения |
т. е. |
|
|
передают атомам |
|
|||
всего 2l+1 значений. Таким образом, магнитное |
|
|||
только |
|
|||
квантовое число ml определяет проекцию |
|
|||
определенные |
|
|||
момента импульса электрона на заданное |
|
|||
порции энергии, причем 4,86 эВ — наименьшая |
|
|||
направление, причем вектор момента импульса |
|
|||
возможная порция энергии (наименьший квант |
|
|||
электрона в атоме может иметь в пространстве |
|
|||
энергии), которая может быть поглощена |
|
|||
2l+1 ориентации. |
|
|
||
атомом ртути в основном энергетическом |
|
|
||
|
|
|
||
состоянии. Следовательно, идея Бора о |
|
|
|
|
существовании в атомах стационарных |
|
|
|
|
состояний блестяще выдержала |
|
|
|
|
экспериментальную проверку. |
|
|
|
|
Спектр излучения атома водорода. |
|
|
|
|

По теории Бора, |
|
|
количественно |
|
|
объяснившей спектр |
|
|
атома водорода, |
|
|
спектральные серии |
|
|
соответствуют |
|
|
излучению, |
|
|
возникающему в |
|
|
результате перехода |
|
|
атома в данное |
|
|
состояние из |
|
|
возбужденных |
|
|
состояний, |
|
|
расположенных |
|
|
выше данного. Спектр поглощения атома |
|
|
водорода является линейчатым, но содержит |
|
|
при нормальных условиях только серию |
|
|
Лаймана. |
|
|
|
|
|
31. Блок-схема лазера. Свойства лазерного |
32. Элементы атомной и ядерной физики. |
|
излучения. |
Протон (р) имеет положительный заряд, равный |
|
Лазер обязательно имеет три основных |
заряду электрона, и массу покоя тр=1,6726 10– |
|
компонента: 1) активную среду, в которой |
27кг 1836 тe, где тe — масса электрона. |
|
создаются состояния с инверсией |
Нейтрон (n) — нейтральная частица с массой |
|
населенностей; 2) систему накачки (устройство |
покоя тп=1,6749 10–27кг 1839 тe. Протоны и |
|
для создания инверсии в активной среде); 3) |
нейтроны называются нуклонами (от лат. |
|
оптический резонатор (устройство, выделя- |
nucleus — ядро). Общее число нуклонов в |
|
ющее в пространство избирательное |
атомном ядре называется массовым числом А. |
|
направление пучка фотонов и формирующее |
Атомное ядро характеризуется зарядом Ze, где Z |
|
выходящий световой пучок). |
— зарядовое число ядра, равное числу протонов |
|
|
в ядре и совпадающее с порядковым номером |
|
|
химического элемента в Периодической системе |
|
|
элементов Менделеева. Ядро обозначается тем |
|
|
же символом, что и нейтральный атом: ZA X , |
|
|
где Х — символ химического элемента, Z |
|
|
атомный номер (число протонов в ядре), А — |
|
|
массовое число (число нуклонов в ядре). Ядра с |
|
|
одинаковыми Z, но разными А (т. е. с разными |
|
Для выделения направления лазерной |
числами нейтронов N=A–Z) называются |
|
изотопами, а ядра с одинаковыми А, но разными |
|
|
генерации используется принципиально важ- |
|
|
Z—изобарами. |
|
|
ный элемент лазера — оптический резонатор. |
|
|
|
|
|
В простейшем случае им служит пара |
|
|
обращенных друг к другу параллельных (или |
|
|
вогнутых) зеркал на общей оптической оси, |
|
|
между которыми помещается активная среда |
|
|
(кристалл или кювета с газом). |
|
|
Лазерное излучение обладает следующими |
|
|
свойствами: |
|
|
1. Временная и пространственная |
|
|
когерентность (см. § 171). Время |
|
|
когерентности составляет 10–3 с, что |
|
|
соответствует длине когерентности порядка 105 |
|
|
м (lког = с ког), т. е. на семь порядков выше, чем |
|
|
для обычных источников света. |
|
|
2. Строгая монохроматичность ( <10–11 м). |
|
|
3. Большая плотность потока энергии. Если, |
|
|
например, рубиновый стержень при накачке |
|
|
получил энергию W=20 Дж и высветился за 10–3 |
|
|
с, то поток излучения Фе=20/10–3 Дж/с=2 104 Вт. |
|
|
Фокусируя это излучение на площади 1 мм2, |
|
|
получим плотность потока энергии Фе/S = |
|
|
2 104/10–6 Вт/м2 = 2 1010 Вт/м2. |
|
|
4. Очень малое угловое расхождение в пучке. |
|
|
|
|
|
