Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Thermodynamics

.pdf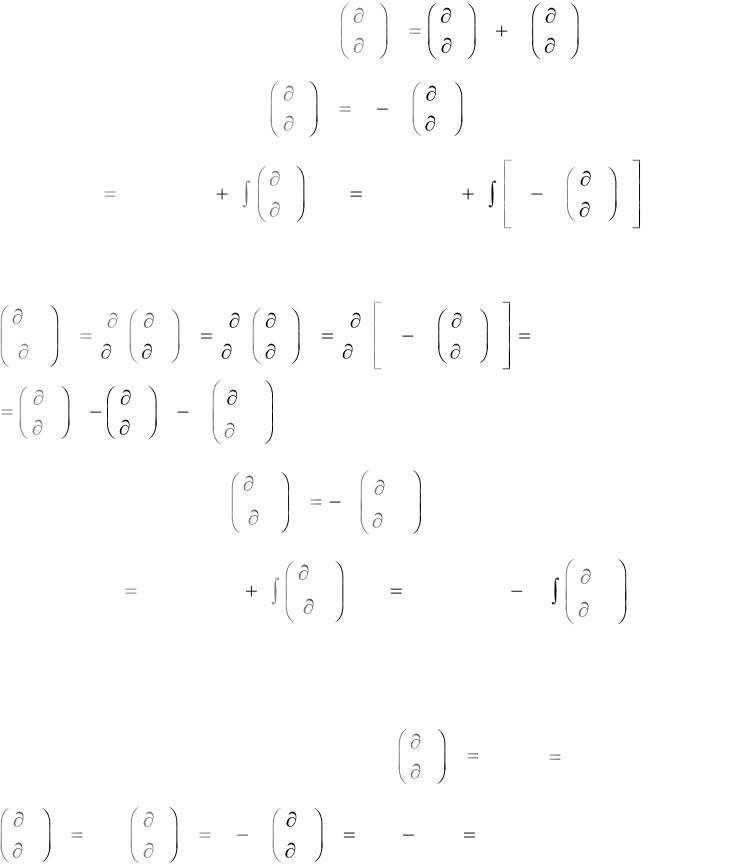

Скачиваний:

Добавлен:

31.03.2015

Размер:

4.5 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

121

2)h = f(T, p);

g = h – Ts; h = g + Ts;

;

p T

; (*)

h(T, p) h0(T, p )

dp h0(T, p )

v T

dp ;

3)cp = f(T, p);

v T

p T

p T p

T p T

T p

;

; (*)

(T, p) c

0(T, p )

dp c

0(T, p ) T

dp ;

Задача. Доказать, что h, u, cp, cv

идеального газа не зависят

от давления.

1) Т.к. h = f(T, p); → доказать, что

0 ;

;

v T

T p

p T

2) u = h - pv = h - RT = f(T);

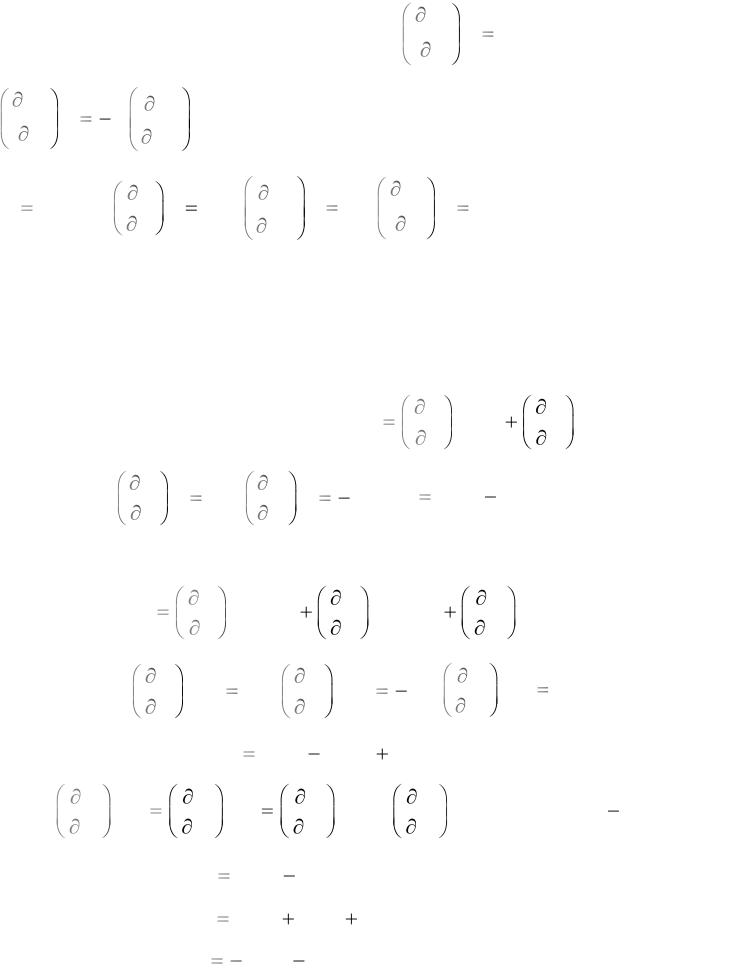
122

3) Т.к. cp = f(T, p);					→ доказать, что	cp	0 ;
3) Т.к. cp = f(T, p);					→ доказать, что	p	0 ;
						p	T
	cp	T	2v	;
	p	T	T 2	;
	p	T	T 2	p
		T		p

;

0 ;

;

T 2

4)cv = cp – R = f(T);

10.3.Термодинамические соотношения для систем

спеременной массой

m = const; U = f(S, V); dU						U	dS		U	dV ;

						S			V
						S	V		V	S
	U	T ;	U	p;	dU TdS			pdV ; (*)

	S		V
	S	V	V	S

m ≠ const; U = f(S, V, m);

dm;

V S,m

V,m

S,V

T ;

φ ;

V,m

V S,m

m S,V

dU TdS

pdV φ dm; (**)

φ = g = h Ts ;

m S,V

m S,p

m T ,V

m T,p

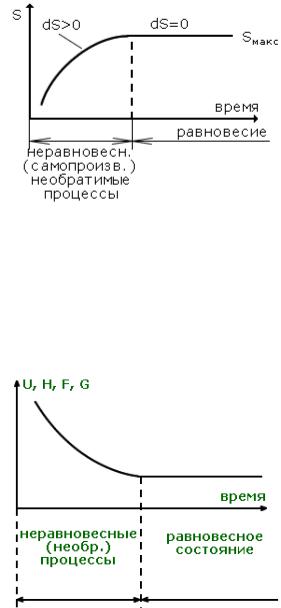
U = f (S, V, m); dU	TdS	pdV + φ dm;
H = f (S, p, m); dH	TdS	Vdp φ dm;

F = f (V, T, m); dF pdV SdT + φ dm;

123

G = f (p, T, m); dG Vdp SdT + φ dm.

124

11.Равновесие термодинамических систем

11.1. Общие условия равновесия термодинамических систем

dQ = dU + pdV; dQ = dH - Vdp; TdS ≥ dQ; 1)Для изолированной системы (U = const, V = const)

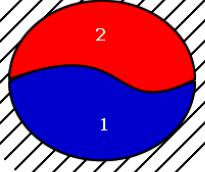
TdS ≥ dU + pdV; → dS ≥ 0;

-для неравновесных процессов

dS > 0; (направление процесса)

-в равновесном состоянии

S = Smax, dS = 0, d2S < 0.	Рис. 11.1.

2)Для системы, у которой S = const, V = const

dU ≤ TdS - pdV; → dU ≤ 0;

-для неравновесных процессов

dU < 0; (направление процесса)

-в равновесном состоянии

U = Umin, dU = 0, d2U > 0.

Рис. 11.2.

3)Для системы, у которой S = const, p = const

125

dH ≤ TdS + Vdp; → dH ≤ 0;

-	для	неравновесных	- в равновесном состоянии:
процессов:			H = Hmin, dH = 0, d2H > 0.
	dH < 0; (направление
		процесса)

	4)Для системы, у которой V = const, T = const
		dF ≤ - SdT - pdV; → dF ≤ 0;

-	для	неравновесных	- в равновесном состоянии
процессов			F = F ; dF = 0; d2F > 0.
			min
	dF < 0; (направление
		процесса)

	5)Для системы, у которой p = const, T = const
		dG ≤ - SdT - pdV; → dG ≤ 0;

-	для	неравновесных	- в равновесном состоянии
процессов			G = G , dG = 0, d2G > 0.
			min
	dG < 0; (направление
		процесса)

11.2. Условия равновесия изолированной системы

dS = 0;

V = V1 + V2 = const; dV1+ dV2 = 0; dV2 = - dV1;

U = U1 + U2 = const; dU1+ dU2 = 0; dU2 = - dU1;

Рис. 11.3.	S = S1	+ S2; dS = dS1+ dS2	= 0;

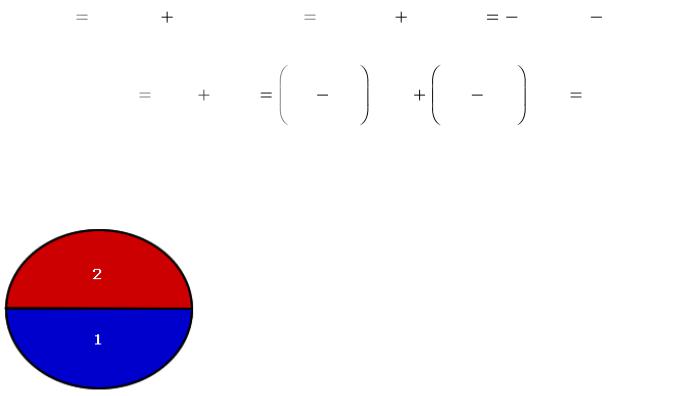
126


dS	1	dU	p1 dV ;		dS		1		dU		p2 dV		1	dU	p2	dV ;

1	1		T1	1	2	2					2	1			1
	T1					T2					T2	T2			T2
	dS dS dS				1			1		dU	p1	p2 dV 0 ;

			1	2	T1	1					T1	1
							T2					T2

T1 = T2; p1 = p2;

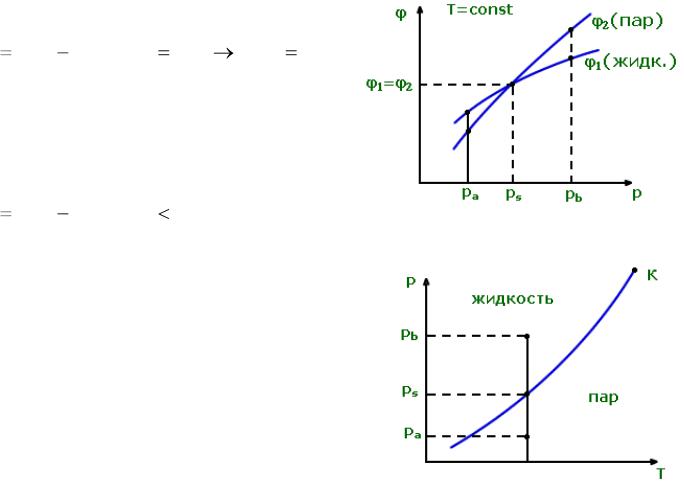
11.3. Условия фазового равновесия

p = const, T = const → dG ≤ 0;

G = G1 + G2; dG = dG1+ dG2 ≤ 0; m = m1 + m2 = const;

dm1+ dm2 = 0; dm2 = –dm1;

Рис. 11.4.

dG1 = V1dp – S1dT + φ1dm1; dG2 = V2dp – S2dT + φ2dm2;

dG = dG1 + dG2 = φ1dm1 + φ2dm2 = (φ1 – φ2)dm1 ≤ 0.

127

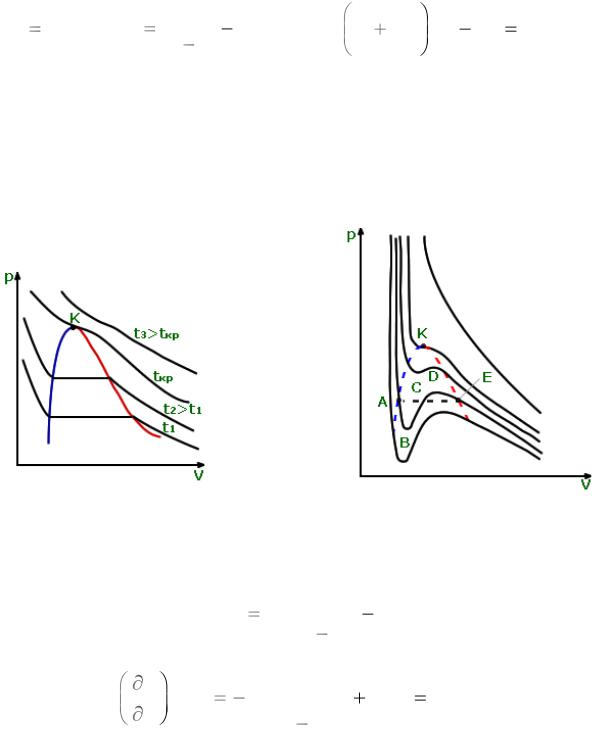
В состоянии равновесия

dG (φ1 φ 2 )dm1 0;

φ1 φ 2;

Правило 1

В неравновесных состояниях

dG (φ1	φ 2 )dm1 0 ;		Рис. 11.5.
			Рис. 11.5.
а) если	φ1 > φ2, то	dm1 < 0,	а
dm2 > 0; → испарение;
б) если	φ1 < φ2, то	dm1 > 0,	а
dm2 < 0;→ конденсация;

Правило 2

Рис. 11.6.

128

12. Термические уравнения состояния

реального газа

12.1. Уравнение Ван-дер Ваальса (1873 г.)

p	RT → p	RT		a	;	p	a	v b RT ;
		v b	v2				v2
	v
		a = const; b = const.
Смысл коэффициентов а и b.
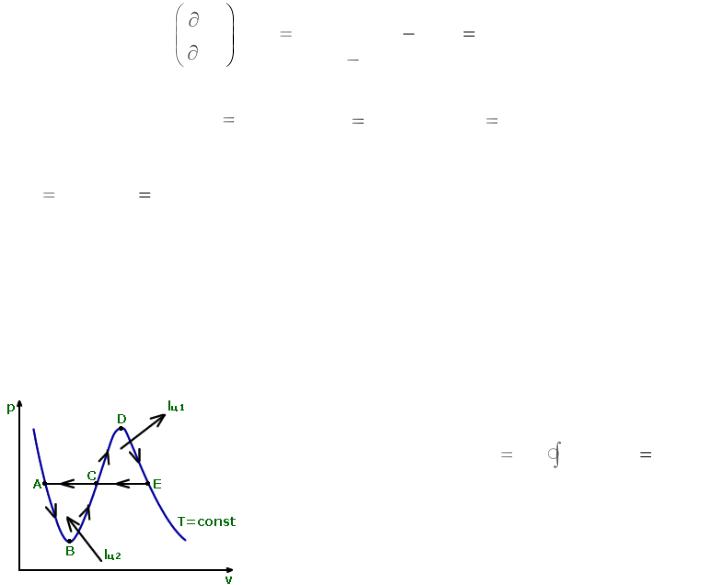
Изотермы Эндрюса						Изотермы Ван-дер-Ваальса

Рис. 12.1.						Рис. 12.2.
						Рис. 12.2.
Корни уравнения
Для критической точки:	p	RTкр			a	;


	кр	vкр	b	vкр2
		vкр	b	vкр2

p	RTкр			2a	0	;
v T ,кр	vкр b	2	v3		0	;
v T ,кр		2	v3
				кр

129

2 p

2RTкр

;

T ,кр

vкр

кр

; T

;

3b;

кр

27b2

кр

27bR

zкр

pкрvкр

0,375

. У реальных газов zкр = 0,22 – 0,33.

RTкр

Определение констант а и b

ркр, Ткр → а1 и b1;

ркр, vкр → а2 и b2;

vкр, Ткр → а3 и b3;

Правило Максвелла

Цикл ABCDEA → lц = 0.

По второму закону lц

pdv 0 ;

ABCDEA

lц = lц1 + lц2 = 0; lц1 > 0; lц2 < 0;

пл. A-B-C-A = пл. С-D-E-C;

Рис. 12.3.

Метастабильные состояния: AB – перегретая жидкость; ED – переохлажденный пар;

BD – физически нереализуемые состояния (т.к. (∂р/∂v)T > 0).

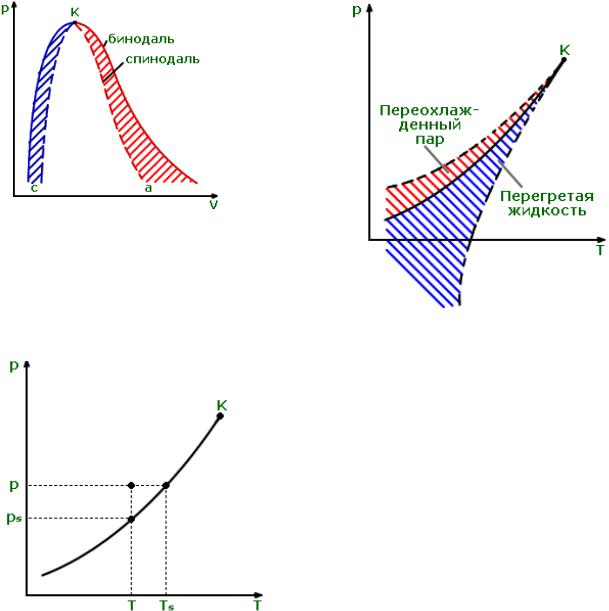
130

Рис. 12.4.

Рис. 12.5.

∆T = Ts – T; – переохлаждение. s = p / ps; – пересыщение.

Рис. 12.5а.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.2015289.28 Кб48teoria.pdf
#
01.03.202544.85 Mб0Test MEEU.doc
#
31.03.201530.5 Кб152test1.docx
#
01.03.2025140.29 Кб0testovyj_kontrol_znanij.doc
#
31.03.20151.18 Mб23Testy_RZA_s_Doc.pdf
#
31.03.20154.5 Mб51Thermodynamics.pdf
#
31.03.201526.11 Кб16Tiitel.doc
#
13.03.2016782.91 Кб7tipar_po_empp мой.docx
#
31.03.20153.18 Mб318Tipovoy_po_ISU_2014.doc
#
31.03.201586.02 Кб33Tipovoy_raschyot_po_elektrostatike_IEE.doc
#
31.03.20153.46 Mб778Tip_rasch_ver.pdf