4.8. Полумарковские процессы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tip_rasch_ver.pdf

Скачиваний:

740

Добавлен:

31.03.2015

Размер:

3.46 Mб

Скачать

☆

<<< < Предыдущая 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 4344 / 4844 45 46 47 48 > Следующая >>>

Вероятность потери поступающей продукции из-за переполнения склада равна u4 (g2 + g3 ) = 0,0725 , т.е. потери составят около7%. Вероятность полного приема на хранение равна 1 - 0,0725 = 0,9275.

Вероятность отгрузки в требуемом объеме равна

u1 + u2 + u3 + u4 + u0 (g1p1 + g2 + g3 ) = 0,9153.

Ответ. 0,9275; 0,9153.

Задача 4.38. Хранилище имеет емкостьK единиц хранения(в нечетных вариантах K = 4 , в четных вариантах K = 5 ). В течение каждого дня в хранилище поступает случайное количествоX единиц продукции. Величины X независимы и имеют одинаковое распределение

		X	0	1	2	3
При		P	g0	g1	g2	g3	поступившей	продукции
При	заполнении		хранилища		избыток		поступившей	продукции

теряется. В конце каждого дня из хранилища отпускается потребителю

случайное число m единиц продукции(или весь				запас,	если он не
превосходит m). Известно, что P(m =1)=			p1, а P(m = =2)	p2.
Для	стационарного	режима	найдите: вероятность		того,	что
поставляемая	продукция	будет полностью(без		потерь)	принята	на

хранение; вероятность того, что отпуск продукции будет производиться в полном объеме.

Величины gi, i = 0,1, 2,3,	возьмите из исходных данных задачи 4.46. В
нечетных вариантах P(m =1)=	p1 = 0,9, а P(m = 2)= p2 = 0,1. В четных

вариантах P(m =1)= p1 = 0,1, а P(m = 2)= p2 = 0,9. (См. пример 4.38.)

работы занятого прибора) = òB(x)l1=e-l1t dt

p = 0; =p 1=– p 1 – b; p= 1;= p = p

Случайный процесс конечным числом состояний называется полумарковским процессом (ПМП), если время пребывания процесса в каждом из состояний случайно и зависит только от этого состояния и от того, в какое состояние затем перейдет процесс.

Пусть Е1, Е2 ,K, Еn –– возможные состояния процесса. Чтобы задать ПМП необходимо указать:

1)матрицу вероятностей переходов || Pij ||, i, j =1, 2,3,K, n;

2)матрицу функций распределения || Fij (x) || , где Fij (x) –– функция

распределения времени пребывания процесса в состоянииЕi при условии, что следующим состоянием будет Еj;

3) начальное распределение {Pi (0)} (например, Р1 (0) =1, Рi (0) = 0 при i ¹1 –– это означает, что процесс начинается из состояния Е1).

349

Заметим, что марковский процесс с непрерывным временем и конечным числом состояний можно считать ПМП, у которого время пребывания в каждом состоянии распределено показательно. Марковскую цепь можно рассматривать в непрерывном времени как ПМП, у которого время пребывания в каждом состоянии равно 1.

Практический интерес представляют многие характеристики ПМП:

1)среднее время достижения состояния Еi из начального состояния;

2)среднее число попаданий в состояние Еi за время t;

3) стационарные вероятности того, что процесс находится в состоянии Еi.

Рассмотрим способы вычисления некоторых характеристик процесса. Если обозначить функцию распределения времени пребывания в состоянии

Еi через Fi (t) = åPij Fij (t), то

j=1

mi = òt dFi (t)

n	¥	ij
å ij	ò	ij
P=		t dF (t)
j=1	0

n	(4.8.1)
P= m ,	(4.8.1)
å ij ij

j=1

где mi –– среднее время		пребывания в состоянииЕi, а		mij	––
математическое ожидание, соответствующее распределению Fij (t).
Обозначим	через Lij ––	среднее время до первого попадания из
состояния Ei в состояние Еj. Легко видеть, что
	Lij = Pij mij + åPik (mik + Lk j )
		k ¹ j
или	Lij = åPik Lk j + åPik mik + Pij mij .
	Lij = åPik Lk j + åPik mik + Pij mij .
	k ¹ j	k ¹ j
Откуда в силу (4.8.1) получаем систему уравнений для определения Lij
	Lij	= åPik Lk j	+ mi .	(4.8.2)
		k ¹ j
Аналогично	можно	провести	рассуждения о среднем		времени

пребывания процесса в множестве состоянийM. Обозначим через m j (M )

среднее время пребывания процесса в множестве состоянийM, если это пребывание началось из состояния Е j ÎМ . Можно показать, что

mj (M ) = å Pik m j (M ) + mi .	(4.8.3)
jÎM
В заключение приведем частичную формулировку одной из важных
теорем о ПМП.
Теорема Пайка (Pyke). Стационарные вероятности	пребывания
процесса в состояниях Еj, j =1,2,K, k равны

350

процессаg(t)

P	=	mju j	,	(4.8.4)
		k
j

åmiui

i=1

где uj –– финитные вероятности вложенной марковской цепи, mi –– среднее

время пребывания	в состоянииЕi, а Рj –– стационарные вероятности
состояний.
Пример 4.39.	Пусть	устройство состоит из трех однотипных
приборов. В момент времени t = 0 начинает работу прибор №1, который
спустя случайное времяТ1		выходит из строя. В этот момент начинает
работу прибор № 2, длительность безотказной работы которого равнаТ2, и
начинается ремонт	прибора	№1, причем время ремонта равноh1. Если

Т2 ³ h1 , то в момент времени Т1 + Т2 начинает работу прибор № 1, а прибор № 2 поступает на ремонт. Если же Т2 < h1 , то начинает работать элемент №

3, а вышедшие из стоя приборы продолжают ремонтироваться в порядке очереди с той же интенсивностью, и т.д. Устройство отказывает, если все три прибора выходят из строя. Предположим, что величины Тi и hj

независимы и имеют соответственно функции распределения F (x) и G(x) . Вычислим среднюю длительность безотказной работы системы(или «наработку на отказ»).

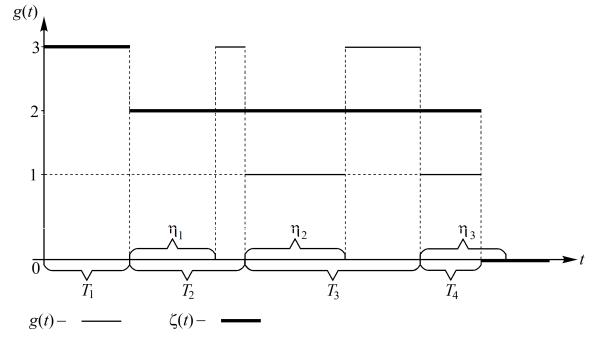
Пусть g(t) –– количество работоспособных приборов в момент времени t. Система начинает работу при трех работоспособных приборах, поэтому при t = 0 имеем g(t) = 3, а в момент, когда g(t) = 0 , устройство выходит из строя. Одна из возможных реализаций изображена на рис. 4.8.1.

351

Рис. 4.8.1

Процесс g(t)

не марковский. Вложим в этот процесс марковскую

цепь, а вместе с нею и полумарковский процессV(t) , следующим образом:

V(t) = 3 при 0 £ t < T1 , а

далее V(t)

равно

состоянию процесса g(t)

после

последнего перед t выхода из строя прибора.

Для

процесса V(t)

в моменты

переходов

из

состояния

в состояние

имеем вероятности переходов

P00 =1,

=P01

P=02

Р=03

P = P(T < h)=

[1 - G= (t )]dF (t) a, P =1 – P =1 – a, P= 0, P= 0,

P = 0, P P= a, P =1 – P 1 – a=, P 0,

P30 = 0,

P31 = 0,

P32= 1,

P33= 0.

Остается вычислить среднюю длительность пребывания системы в

множестве

состояний М ={3, 2;1}

при

условии, что

функционирование

системы начинается

из

состоянияg(0) = 3 , т.е. наработка на

отказ

равна

m3 (M ) . Последнюю величину можно найти из системы уравнений, которая

согласно (4.8.2) имеет вид:

m3 (M ) = P33m3 (M ) + P32m2 (M ) + P31m1 (M ) + m3 ,

m2 (M ) = P23m3 (M ) + P22m2 (M ) + P21m1 (M ) + m2 ,

m (M ) = P m (M ) + P m (M ) + P m (M ) + m .

С учетом значений вероятностей переходовPij

и того, что математи-

ческие ожидания m1 = m2 = m3 = m , получаем

m1 (M ) =

, m2

(M ) =

m3 (M ) = m

P =

m +

ò[1 - G(t)]dF (t)

Ответ. m3 (M ) = m +

ò[1 - G(t)]dF (t)

Задача

4.39.

Пусть

устройство

состоит

из

двух

однотипных

приборов. В момент времени t = 0

начинает работу прибор №1, который

спустя случайное времяТ1

выходит из строя. В этот момент начинает

работу прибор № 2, длительность безотказной работы которого равнаТ2, и

начинается

ремонт

прибора

№1, причем

время ремонта равноh1. Если

Т2 ³ h1 , то в момент времени Т1 + Т2

начинает работу прибор № 1, а прибор

№ 2 поступает

на

ремонт. Если же Т2 < h1 ,

т.е. оба

прибора

вышли из

строя, то устройство отказывает, а вышедшие из стоя приборы продолжают

ремонтироваться в

порядке

очереди

той

же

интенсивностью, т.д.

352

Предположим, что величины Тi		и hj		независимы и имеют соответственно
функции распределения
	ì0		при x < 0,
	ï		a2
F (x) = í			a2			при x ³ 0
	ï1	-
	ï1	-	(x + a)		2
и	î		(x + a)
и
ì0	при x <1,
ï				при 1 £ x < (a + 2) / 2,
G(x) = í4(x -1)2 / a2				при 1 £ x < (a + 2) / 2,
ï	при (a + 2) / 2 £ x.
î1	при (a + 2) / 2 £ x.

Вычислите среднюю длительность безотказной работы системы(или «наработку на отказ»). (См. пример 4.39, a –– номер варианта.)

Пример 4.40. В одноканальную систему с потерями поступает

простейший поток требований	интенсивностиl. Времена	обслуживания
независимы и каждое имеет некоторое распределение B(x) . В любой момент
времени обслуживающий прибор	может отказать. Если прибор свободен, то
время его безотказной работы в этом состоянии		имеет показательное

распределение с параметром l0. Время безотказной работы прибора, занятого
обслуживанием, тоже имеет показательное распределение, но с параметром
l1. Отказавший			прибор	тотчас	начинают	ремонтировать				и	время
восстановления			имеет	распределениеR(x) . При			отказе		прибора
обсуживаемое требование теряется, а новые требования не принимаются до
окончания ремонта. Все названные величины стохастически независимы.
Необходимо найти среднее время пребывания						системы			в	отказном
состоянии.
Решение. Будем различать состояниеE0, в котором обслуживающий
прибор исправен и свободен, состояние E1, в котором прибор обслуживает
требование, состояние E2, в котором прибор неисправен и ремонтируется.
Пусть q(t) –– состояние				системы в момент времениt.			Процесс		q(t)
является полумарковским. Назовем его характеристики.
1. Переходные вероятности:
p00 = 0;
p01 = P (того, что требование поступит в свободную систему ранее,
				¥		l
чем прибор выйдет из строя) = ò(1 - e-lt )l0e-l0t dt =						l		;
чем прибор выйдет из строя) = ò(1 - e-lt )l0e-l0t dt =								;
	l0			0		l + l0
p02 =1 – p01 =	l0		;
p02 =1 – p01 =	l + l	0	;
		0

p01 = P (того, что время обслуживания меньше времени безотказной

353

Итак, переходная матрица имеет вид:

æ0 l / (l + l0 ) l0			/ (l + l0 ) ö
ç		0	1 - b	÷
çb				÷.
ç	1	0	0	÷
è				ø

Запишем уравнения для финитных вероятностей вложенной цепи:

u = bu + u

; =u

= l

u ; u

+ (1 – b)u .

l + l

Из первого и второго уравнений следует, что u2 = u0 ç1 – b

÷. Поэтому из

l + l0 ø

условия нормировки u0

u0 + u0 ç1 – b

=1 получаем, что

l + l

0 ø

l + l0

+ l / (l + l0 ) +1 - bl / (l + l0 ) 3l +

2l0 - bl

l / (l + l0 )

1 + l / (l + l0 )

+[1 - bl / (l + l0 )] 3l + 2l0 - bl

1 - bl / (l + l0 )

l + l0 - bl

+ l / (l + l0 ) +[1 - bl / (l + l0 )] 3l + 2l0 - bl

2. Вычислим

теперь

среднее

время пребывания в каждом из

состояний. Время пребывания в состоянииE0

равно минимальному из

времени паузы и времени безотказной работы свободного прибора. Пусть

X –– время пребывания в состоянииE0, X0 –– время безотказной работы в

ненагруженном

состоянии,

а X1 –– время

до

прихода

ближайшего

требования. Тогда X имеет функцию распределения

F (x) = P( X < x) = P[min( X 0 , X1) < x] =1 – P[min( X 0 , X1) > x] =

=1 - P[ X0 > x, X1 > x=] 1=– e-l0 xe-l1x

1 - e-(l0 +l1 ) x .

Это показательный

закон

распределения

параметромl + l .

Поэтому среднее время пребывания в состоянииE0

равно m = (l

+ l )-1.

Время пребывания в состоянии E1 равно минимуму времени обслуживания и времени выхода из строя занятого прибора. Поэтому

m1 = ò[1 - B(t)] e-l1t dt.

354

Это равенство получается из следующих соображений. Если X ––

неотрицательная	случайная	величина	с	функцией	распределения
F (x) = P( X < x), то
	¥	¥
	M ( X ) = òP( X > x) dx= ò[1 - F (x)]dx,				(4.8.5)
	0	0
в этом можно убедиться, взяв по частям интеграл в правой части равенства.
Пусть T –– время пребывания системы в состоянииE1, V –– время
обслуживания, W –– время		безотказной работы прибора в занятом
состоянии. Тогда T = min{V ,W } . Так как P(V > x) =1 – B(x), а P(W > x) =
= exp(–l1 x), то
		¥
	m1 = M (T )= òP(T > x) dx =
¥	¥	0		¥
¥	¥			¥
= òP(min(V ,W ) > x) dx = òP(V > x и W > x)dx = ò[1 - B(t)] e-l1t dt.
0	0			0

Время пребывания в состоянииE3 равно времени ремонта. Поэтому

m2 = mR = òtdR(t).

Доля времени пребывания в отказном состоянии равна стационарной вероятности состояния E2. По формуле (4.8.4) эта стационарная вероятность равна

P	=		m2u2			=			m2 (l + l0 - bl)				.
P	=					=							.
2			2				(l + l0 ) / (l + l1 ) + m1l + m2 (l + l0 - bl)
							(l + l0 ) / (l + l1 ) + m1l + m2 (l + l0 - bl)
			åmiui
			i=0				m2 (l + l0 - bl)
Ответ.							m2 (l + l0 - bl)					.
Ответ.		(l + l		0	) / (l + l ) + m l + m (l + l					0	- bl)	.
				0	1			1	2	0

Задача 4.40. В одноканальную систему с потерями поступает простейший поток требований интенсивностиl . Времена обслуживания независимы и каждое имеет показательное распределение с параметром .ν В любой момент времени обслуживающий прибор может отказать. Если прибор свободен, то время его безотказной работы в этом состоянии имеет показательное распределение с параметромl0. Время безотказной работы

прибора, занятого обслуживанием, тоже имеет показательное распределение, но с параметром l1. Отказавший прибор тотчас начинают ремонтировать, и время восстановления имеет распределение

ì0 при x <1,

ï		£ x < e,
R(x) = íln x при 1
ï	£ x.
î1 при 1

355

При отказе прибора обсуживаемое требование теряется, а новые

требования	не принимаются до окончания ремонта. Все	названные
величины стохастически независимы.
Необходимо найти среднее время пребывания системы в отказном
состоянии. (См. пример 4.40, если N –– номер варианта, то		l = N / 15,
n = N / 10 ,	l0 = N / 100 , l1 = N / 50.)

356

<<< < Предыдущая 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 4344 / 4844 45 46 47 48 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.20154.5 Mб44Thermodynamics.pdf
#
31.03.201526.11 Кб14Tiitel.doc
#
13.03.2016782.91 Кб5tipar_po_empp мой.docx
#
31.03.20153.18 Mб318Tipovoy_po_ISU_2014.doc
#
31.03.201586.02 Кб33Tipovoy_raschyot_po_elektrostatike_IEE.doc
#
31.03.20153.46 Mб740Tip_rasch_ver.pdf
#
31.03.201528.16 Кб12Titul_Razdatochnyy_material.doc
#
31.03.2015144.38 Кб22TPI_Zadania_14.doc
#
31.03.201588.06 Кб23tr1_dlya_enmi_2012.doc
#
31.03.20157.49 Mб8tr2(2014-1)gox.doc
#
31.03.2015825.55 Кб52tr3.pdf