3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

3.1. Точечные оценки

3.1.1. Свойства оценок

Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого e > 0

n®¥

Р(| а%( Х1, Х 2 ,K, Х n ) - a | < e) ¾¾¾®1.

175

Если известно, что оценка а% несмещенная, то для ее состоятельности достаточно, чтобы

n®¥

D(а%( Х1, Х 2 ,K, Х n )) ¾¾¾®0.

Последнее условие удобно для проверки.

В качестве меры разброса значений оценки а% относительно а можно рассматривать величину М (а% - а)2. Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру

желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней

результаты n независимых наблюдений случайной величины, то в качестве

оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений

176

=1 ån ( X i - m)2 - ( X - m)2. n i=1

n

несмещенной оценки введем поправку в виде множителя и n -1

полученную оценку обозначим через s2:

Величина

n

å( X i - X )2

является несмещенной и состоятельной оценкой дисперсии.

Пример 3.1. Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.

Решение. По формулам (3.1.1) и (3.1.3) имеем

177

Ответ. М ( X ) » 5; D( X ) » 4,17.

Задача 3.1. Оцените математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений. (См. пример 3.1; в качестве исходных данных возьмите данные к задаче 3.22.)

Пример 3.2. Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:

Требуется оценить математическое ожидание и дисперсию этой случайной величины.

Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы(3.1.1) и (3.1.3) дают следующие оценки:

Задача 3.2. По сгруппированным данным результатов наблюдений случайной величины оцените математическое ожидание и дисперсию этой случайной величины. (См. пример 3.2; в качестве исходных данных возьмите данные к задаче 3.12.)

3.1.3. Метод наибольшего правдоподобия для оценки параметров распределений

В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон

178

характеристик. Поэтому практический интерес представляет следующая задача.

Пусть случайная величина Х имеет функцию распределения F (x, q), причем тип функции распределенияF известен, но неизвестно значение параметра q. По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.

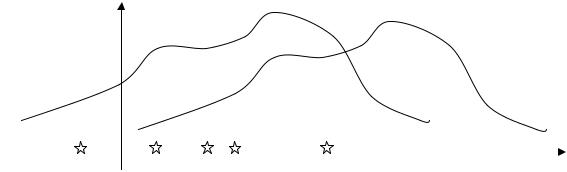
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций

Х

Рис. 3.1.1

Из рисунка видно, что при значении параметраq2 такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же q1 эти результаты наблюдений вполне возможны. Поэтому значение

качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.

Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величиныХ зависит от неизвестного значения параметра q. Обозначим через Р(х,q) для непрерывной случайной величины плотность вероятности в точкех, а для дискретной случайной величины –– вероятность того, что Х = х. Если в n независимых наблюдениях реализовались значения случайной величиныХ1, Х 2 ,K, Х n , то выражение

называют функцией правдоподобия. Величина L зависит только от параметра q при фиксированных результатах наблюдений Х1, Х 2 ,K, Х n . При каждом

значении параметра q функция L равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе

179