2.ТЕОРИЯ ВЕРОЯТНОСТЕЙ
2.1.Классическое определение вероятности
Классическое определение вероятности. Если исходы опыта
равновозможны, то вероятностью события A называется отношение числа исходов, благоприятствующих данному событию, к числу всех возможных исходов опыта, т.е.
P( A) = m , n
где m –– число исходов опыта, благоприятствующих событию, а n –– число всех возможных исходов.
Свойства вероятностей.
1. Вероятность любого события –– есть число, заключенное между нулем и единицей, т.е. 0 £ P( A) £1. Вероятность невозможного события равна 0, а вероятность достоверного события равна 1.
2. Если события A и B несовместны, то P( A + B) P=( A) + P(B).
3. Вероятность любого события A в сумме с вероятностью противо-
положного события A равна единице: P( A) + P( A) =1.
Если вероятность интересующего нас событияA по каким-либо причинам вычислить трудно, то можно попытаться вычислить вероятность противоположного события, а затем с помощью свойства3 вычислить искомую вероятность события A.
Пример 2.1. Брошены две игральные кости. Найти вероятности следующих событий:
A –– на обеих костях выпало одинаковое число очков; B –– сумма числа очков не меньше 11;
C –– число очков на первой кости больше, чем на второй; D –– сумма очков четная;
E –– сумма числа очков больше трех.
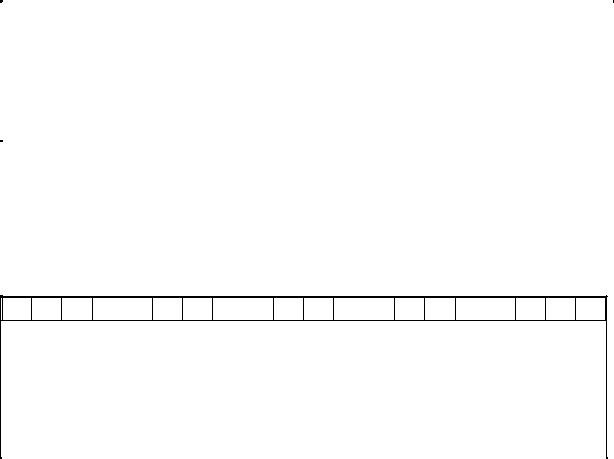
Решение. Число очков, благоприятствующих каждому из названных событий, легко подсчитать, если все возможные исходы опыта перечислить в виде табл. 2.1.1. В каждой клетке таблицы первая цифра указывает число очков на первой кости, вторая –– на второй кости.
Таблица 2.1.1
11 |
12 |
13 |
14 |
15 |
16 |
21 |
22 |
23 |
24 |
25 |
26 |
31 |
32 |
33 |
34 |
35 |
36 |
41 |
42 |
43 |
44 |
45 |
46 |
51 |
52 |
53 |
54 |
55 |
56 |
18
|
|
61 |
62 |
|
63 |
64 |
65 |
66 |
|
|
Если кости симметричны и однородны, то все перечисленные исходы |
||||||||||
опыта |
равновозможны. |
Тогда |
P( A) = 6 / 36 =1 |
/ 6 (благоприятствуют |
||||||
исходы: 11, 22, 33, 44, 55, 66), P(B) = 3 / 36 =1 / 12 |
(благоприятствуют три |
|||||||||
исхода: 56, 65, 66) Непосредственный подсчет числа благоприятствующих исходов дает P(C) =15 / 36 = 5 / 12, P(D) =18 / 36 =1 / 2, P(E) = 33 / 36 =
=11 / 12.
Ответ. P( A) =1 / 6, P(B) =1 / 12, P(C) = 5 / 12, P(D) =1 / 2, P(E) =11 / 12.
Задача 2.1.1. Брошены две игральные кости. Для вариантов 1–10 найти вероятности следующих событий:
A –– сумма числа очков не превосходит N;
B –– произведение числа очков превосходит N;
C –– произведение числа очков делится на N.
(См. пример 2.1, N равно последней цифре номера варианта плюс 2). Для вариантов 11–20 найти вероятности следующих событий:
A –– сумма числа очков не меньше N;
B –– произведение числа очков меньше N; C –– сумма числа очков делится на N.
(См. пример 2.1, N равно последней цифре номера варианта плюс 3). Для вариантов 21–30 найти вероятности следующих событий:
A –– сумма числа очков равна N;
B –– произведение числа очков больше N; C –– сумма числа очков делится на N.
(См. пример 2.1, N последняя цифра номера варианта плюс 4).
Задача 2.1.2. Из чисел 1, 2,3,K, n наугад взяли одно число, затем второе.
Какова вероятность того, что первое число меньше второго? Какова вероятность того, что оба числа больше n/2? Найдите вероятность того, что будут выбраны равные числа.
Какова вероятность того, что сумма этих чисел окажется меньше n? Какова вероятность того, что первое число окажется на2 больше
второго?
Какова вероятность того, что первое число окажется меньше3, а второе больше (n - 3) ?
Решите задачу в случае бесповторного и в случае повторного выбора. (См. пример 2.1, n –– номер варианта плюс 3).
19
Пример 2.2. а) В урне содержится N шаров, из них R красного цвета. Наугад выбрано n шаров. Какова вероятность того, что r из них окажутся красного цвета? Какова вероятность того, что среди выбранных шаров хотя бы один будет красным?
б) Из партии, содержащей 10 изделий, среди которых три бракованных, наугад извлекаются три изделия для контроля. Найти вероятности следующих событий:
A –– среди выбранных изделий ровно два бракованных; B –– выбраны только бракованные изделия;
C –– среди выбранных изделий содержится хотя бы одно бракованное.
Решение. )а Если |
шары |
тщательно |
перемешаны |
и |
выбираются |
наугад, то равновозможен выбор |
любыхn шаров. Поэтому |
применимо |
|||
классическое определение вероятности. Поскольку выбор бесповторный и |
|||||
нас интересует только состав, то |
выбрать |
любыеn шаров |
можно СNn |
||
способами. Сформировать выборку требуемого состава можно, если из R |
|||||
красных шаров выбрать любые r шаров (это можно сделать СRr |
способами) |
||||
и к ним добавить(n – r) |
любых |
не красных шаров(это можно |
сделать |
||
СNn--rR способами).
По комбинаторному принципу число благоприятствующих исходов равно СRr СNn--rR . Искомая вероятность равна
P |
= |
Сr Cn-r |
|
|
R N -R |
. |
(2.1.1) |
||
|
||||
n,r |
|
CNn |
|
|
Пусть Ai означает наличие в выборкеi красных шаров. Выбор хотя
бы одного красного шара равносилен появлению хотя бы одного из несовместных событий Ai или A2 или … или An. Поэтому вероятность выбора хотя бы одного красного шара равна
Cn -
Pn,1 + Pn,2 +K+ Pn,n 1=– Pn,0 1=– N n R .
CN
б) Выбрать любых три изделия из10 можно С103 способами. Поэтому имеем С103 =120 равновозможных исходов.
Событию A благоприятствуют те исходы, при которых из семи годных изделий выбирается одно (это можно сделать С71 = 7 способами) и
из трех бракованных–– два (это можно сделать С32 = 3 способами). По комбинаторному принципу число благоприятствующих событию A исходов
равно С1С2 |
= 7 ×3 = 21. Поэтому P( A) = 21 / 120= 7 / 40 »1 / 6, т.е. примерно |
|
7 |
3 |
|
один шанс из шести.
Событию B благоприятствует всего один исход и его вероятность
P(B) =1 / 120.
20
Вероятность события C проще вычислить, определив сначала
вероятность события С , которое состоит в том, что выбраны все годные изделия. Выбрать три годных изделия из семи можноС73 = 35 способами.
Поэтому P(С) = 35 / 120 и
P(C) =1 – P(С=) 1 – 35=/ 120 17 / 24 » 2 / 3.
Сr Cn-r
Ответ. а) R N -R
CNn
C n -
, 1 - N R ;
CNn
б) P( A) = 7 / 40 »1 / 16, P(B) =1 / 120, P(C) =17 / 24 » 2 / 3.
Задача 2.2.1. Из N изделий М имеют скрытый дефект. Наугад выбрано n изделий. Найдите вероятности следующих событий:
A –– среди выбранных m изделий имеют скрытый дефект;
B –– среди выбранных есть хотя бы одно изделие со скрытым дефектом;
C –– среди выбранных не более двух изделий со скрытым дефектом. (См. пример 2.2 и исходные данные.)
Исходные данные к задаче 2.2.1.
№ N M n m 
№ N M n m 
№ N M n m
1 |
10 |
3 |
4 |
2 |
11 |
12 |
4 |
3 |
2 |
21 |
9 |
5 |
4 |
2 |
2 |
10 |
3 |
5 |
2 |
12 |
12 |
4 |
4 |
2 |
22 |
9 |
5 |
4 |
3 |
3 |
10 |
4 |
3 |
2 |
13 |
12 |
4 |
4 |
3 |
23 |
11 |
3 |
3 |
2 |
4 |
10 |
4 |
4 |
2 |
14 |
12 |
5 |
3 |
2 |
24 |
11 |
3 |
4 |
2 |
5 |
10 |
4 |
4 |
3 |
15 |
12 |
5 |
4 |
2 |
25 |
11 |
3 |
4 |
3 |
6 |
12 |
3 |
3 |
2 |
16 |
9 |
3 |
3 |
2 |
26 |
11 |
4 |
3 |
2 |
7 |
12 |
3 |
4 |
2 |
17 |
9 |
4 |
3 |
2 |
27 |
11 |
4 |
4 |
2 |
8 |
12 |
3 |
4 |
3 |
18 |
9 |
4 |
4 |
2 |
28 |
11 |
4 |
4 |
3 |
9 |
12 |
3 |
5 |
2 |
19 |
9 |
4 |
4 |
3 |
29 |
14 |
3 |
3 |
2 |
10 |
12 |
4 |
5 |
3 |
20 |
9 |
5 |
3 |
2 |
30 |
14 |
3 |
4 |
2 |
Задача 2.2.2. В урне содержится 2n шаров, из которых два черных, а остальные белые. Наугад выбирается n шаров. Найдите вероятности следующих событий:
A –– в числе выбранных оказались оба черных шара; B –– ни один из черных шаров не выбран;
C –– среди выбранных шаров только один черный шар.
Найдите значения этих вероятностей приn ® ¥ . (См. пример 2.2, n = k + 2 , где k –– номер варианта.)
Задача 2.2.3. В урне содержитсяn1 белых и n2 черных шаров. Из урны наугад выбирают два шара. Что вероятнее –– вынуть два белых шара
21
или вынуть один белый и один черный шар? (См. пример 2.2 и исходные данные.)
Исходные данные к задаче 2.2.3.
№ |
n1 |
n2 |
№ |
n1 |
n2 |
№ |
n1 |
n2 |
|
№ |
n1 |
n2 |
|
№ |
n1 |
n2 |
№ |
n1 |
n2 |
1 |
4 |
2 |
6 |
6 |
3 |
11 |
7 |
3 |
|
16 |
8 |
3 |
|
21 |
9 |
4 |
26 |
10 |
3 |
2 |
4 |
3 |
7 |
6 |
4 |
12 |
7 |
4 |
|
17 |
8 |
5 |
|
22 |
9 |
5 |
27 |
10 |
4 |
3 |
5 |
2 |
8 |
6 |
5 |
13 |
7 |
5 |
|
18 |
8 |
6 |
|
23 |
9 |
6 |
28 |
10 |
5 |
4 |
5 |
3 |
9 |
6 |
6 |
14 |
7 |
6 |
|
19 |
9 |
2 |
|
24 |
9 |
7 |
29 |
10 |
6 |
5 |
6 |
2 |
10 |
7 |
2 |
15 |
8 |
2 |
|
20 |
9 |
3 |
|
25 |
10 |
2 |
30 |
10 |
7 |
|
Задача 2.2.4. В урне m1 белых, |
m2 синих и m3 |
красных шаров. Наугад |
||||||||||||||||
выбирают 6 шаров. Найдите вероятности следующих событий: A –– среди выбранных только белые шары; B –– среди выбранных нет красных шаров; C –– среди выбранных поровну шаров всех цветов; D –– среди выбранных только один красный шар. (См. пример 2.2 и исходные данные.)
Исходные данные к задаче 2.2.4.
№ m1 m2 m3 
№ m1 m2 m3 
№ m1 m2 m3 
№ m1 m2 m3 
№ m1 m2 m3
1 |
8 |
3 |
4 |
7 |
7 |
3 |
5 |
13 |
9 |
4 |
3 |
19 |
8 |
5 |
3 |
25 |
9 |
5 |
2 |
2 |
8 |
4 |
3 |
8 |
7 |
5 |
3 |
14 |
9 |
3 |
3 |
20 |
8 |
2 |
6 |
26 |
9 |
5 |
4 |
3 |
8 |
2 |
5 |
9 |
7 |
4 |
4 |
15 |
9 |
3 |
5 |
21 |
8 |
6 |
2 |
27 |
9 |
4 |
5 |
4 |
6 |
5 |
2 |
10 |
8 |
2 |
3 |
16 |
9 |
5 |
3 |
22 |
9 |
3 |
4 |
28 |
9 |
3 |
6 |
5 |
7 |
2 |
6 |
11 |
9 |
4 |
2 |
17 |
8 |
4 |
4 |
23 |
9 |
2 |
5 |
29 |
9 |
6 |
3 |
6 |
7 |
6 |
2 |
12 |
9 |
3 |
4 |
18 |
8 |
3 |
5 |
24 |
9 |
4 |
3 |
30 |
9 |
2 |
7 |
Задача 2.2.5. Из N билетов с номерами от 1 до N один за другим (без возвращения) берут два билета. Найдите вероятности следующих событий:
A –– оба номера билетов четные; B –– оба номера нечетные;
C –– номер первого билета четный, а второго нечетный; D –– номер одного четный, а другого нечетный:
E –– номер второго билета четный.
(См. пример 2.2, N –– номер варианта плюс 5.)
Задача 2.2.6. В урне содержатся шары с номерами1, 2,3,K, n. Наугад без возвращения выбираютk шаров. Какова вероятность того, что будут выбраны только шары с номерами большеk? Какова вероятность того, что для каждого из первыхk шаров номер шара совпадет с его номером по порядку извлечения? (См. пример 2.2 и исходные данные.)
22
Исходные данные к задаче 2.2.6.
№ |
n |
k |
№ |
n |
k |
№ |
n |
k |
№ |
n |
k |
№ |
n |
k |
№ |
n |
k |
1 |
7 |
3 |
6 |
10 |
3 |
11 |
11 |
4 |
16 |
13 |
3 |
21 |
14 |
4 |
26 |
15 |
5 |
2 |
8 |
3 |
7 |
10 |
4 |
12 |
12 |
3 |
17 |
13 |
4 |
22 |
14 |
5 |
27 |
15 |
6 |
3 |
8 |
4 |
8 |
10 |
5 |
13 |
12 |
4 |
18 |
13 |
5 |
23 |
14 |
6 |
28 |
16 |
3 |
4 |
9 |
3 |
9 |
11 |
3 |
14 |
12 |
5 |
19 |
13 |
6 |
24 |
15 |
3 |
29 |
16 |
4 |
5 |
9 |
4 |
10 |
11 |
5 |
15 |
12 |
6 |
20 |
14 |
3 |
25 |
15 |
4 |
30 |
16 |
5 |
Пример 2.3. При раздаче тщательно перемешанных карт (в колоде 36 карт) игрок получает шесть карт. Какова вероятность того, что игрок получит два туза, два короля и две дамы любой масти?
Решение. Шесть карт данному игроку можно сдатьС366 способами, так как выбор бесповторный и нас интересует только состав выбора. Выбрать два туза, два короля и две дамы можноС42С42С42 = 63 = 216 способами.
Поэтому искомая вероятность равна P = 216 / С366 = 9 / 2618 » 0,003 .
Ответ. 9 / 2618 » 0,003.
Задача 2.3. В урне смешаныN1 шаров белого цвета, N2 шаров черного цвета, N3 –– синего и N4 –– красного. Наугад выбрано n шаров. Какова вероятность того, что среди выбранных ровно n1 белых, n2 черных, n3 синих иn4 красных шаров ( n = n1 + n2 + n3 + n4 )? (См. пример 2.3 и исходные данные.)
Исходные данные к задаче 2.3.
№ |
N1 |
N2 |
N3 |
N4 |
n1 |
n2 |
n3 |
n4 |
№ |
N1 |
N2 |
N3 |
N4 |
n1 |
n2 |
n3 |
n4 |
1 |
2 |
4 |
1 |
3 |
1 |
2 |
1 |
2 |
16 |
3 |
4 |
2 |
3 |
2 |
2 |
1 |
2 |
2 |
2 |
4 |
1 |
3 |
1 |
3 |
1 |
2 |
17 |
4 |
3 |
2 |
3 |
2 |
1 |
1 |
2 |
3 |
2 |
2 |
4 |
3 |
1 |
1 |
2 |
2 |
18 |
2 |
4 |
2 |
3 |
2 |
3 |
1 |
2 |
4 |
2 |
2 |
4 |
3 |
1 |
2 |
1 |
2 |
19 |
2 |
4 |
2 |
3 |
1 |
1 |
2 |
2 |
5 |
2 |
2 |
4 |
3 |
1 |
2 |
2 |
2 |
20 |
2 |
4 |
2 |
3 |
1 |
2 |
1 |
2 |
6 |
2 |
4 |
2 |
3 |
1 |
2 |
2 |
2 |
21 |
4 |
2 |
3 |
2 |
2 |
1 |
1 |
1 |
7 |
2 |
4 |
2 |
3 |
2 |
2 |
1 |
2 |
22 |
4 |
2 |
3 |
2 |
3 |
1 |
1 |
2 |
8 |
2 |
4 |
2 |
3 |
2 |
1 |
2 |
1 |
23 |
4 |
3 |
3 |
2 |
2 |
1 |
2 |
1 |
9 |
2 |
4 |
2 |
3 |
1 |
3 |
1 |
2 |
24 |
4 |
2 |
3 |
3 |
2 |
1 |
1 |
2 |
10 |
2 |
4 |
2 |
3 |
1 |
2 |
1 |
2 |
25 |
4 |
3 |
3 |
2 |
3 |
2 |
1 |
2 |
11 |
3 |
1 |
4 |
2 |
2 |
1 |
2 |
1 |
26 |
4 |
4 |
3 |
2 |
2 |
2 |
1 |
1 |
12 |
3 |
1 |
4 |
2 |
2 |
1 |
3 |
1 |
27 |
2 |
3 |
3 |
5 |
1 |
2 |
1 |
2 |
13 |
3 |
1 |
4 |
2 |
2 |
1 |
2 |
2 |
28 |
3 |
2 |
3 |
5 |
1 |
2 |
2 |
2 |
14 |
2 |
4 |
2 |
3 |
1 |
2 |
2 |
2 |
29 |
3 |
5 |
2 |
4 |
2 |
1 |
1 |
1 |
15 |
2 |
4 |
2 |
3 |
1 |
3 |
1 |
2 |
30 |
3 |
3 |
2 |
5 |
2 |
1 |
1 |
3 |
23
Пример 2.4. В течение недели независимо друг от друга происходят четыре события. Найдите вероятности следующих событий:
A –– все четыре события произойдут в разные дни недели; B –– все четыре события произойдут в один день;
C –– все эти события произойдут в последние три дня недели;
D –– хотя бы в один день недели произойдут два или более из этих событий.
Решение. Дни недели можно представить в виде ящиков, а события в
виде |
шариков. |
Тогда распределение событий по дням недели можно |
|||||
считать раскладкой шариков по ящикам. |
|
|
|||||
Так как каждый из четырех шариков можно поместить в любой из |
|||||||
семи ящиков, то существует 74 = 2401 равновозможный способ разложить |
|||||||
четыре |
|
шарика |
по семи ящикам. Из них событиюA благоприятствуют |
||||
7 × 6 ×5 × 4 = 840 |
способов, так как для каждого последующего шарика |
||||||
остается на один пустой ящик меньше. Поэтому P( A) = |
840 |
|
» 0,35. |
||||
|
|
||||||
|
|
|
|
2401 |
|||
Событию |
B благоприятствует всего семь |
способов. Поэтому |
|||||
P(B) = |
7 |
= 1 |
» 0,003. |
|
|
|
|
|
|
|
|
||||
|
74 |
343 |
|
|
|
|
|
Все четыре события могут произойти в последние три дня недели34 |
|||||||
способами. Поэтому P(C) = |
34 |
» 0,038. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
74 |
|
|
|
|
|
|
|
|||||
|
Событие D противоположно событию A. Поэтому P(D) =1 |
- P( A) = |
||||||||||
=1 – |
840 |
»1 - 0,35 = 0,65. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
2401 |
840 |
|
|
|
1 |
|
|
81 |
|
|
||
|
Ответ. P( A) = |
» 0,35, P(B) = |
» 0, 003, |
P(C) = |
|
» 0,038, |
||||||
|
|
|
|
|||||||||
2401 |
|
|
343 |
2401 |
|
|||||||
P(D) = 0,65. |
|
|
|
|
|
|
|
|||||
Задача 2.4. В лифт k-этажного дома селиm пассажиров. Каждый пассажир независимо от других с равной вероятностью может выйти на любом этаже, начиная со второго. Найти вероятности следующих событий:
A –– все пассажиры вышли на разных этажах; B –– все вышли выше четвертого этажа;
C –– никто не вышел на пятом этаже;
D –– хотя бы два вышли на одном этаже. (См. пример 2.4 и исходные данные.)
24
Исходные данные к задаче 2.4.
№ k m 
№ k m 
№ k m 
№ k m 
№ k m 
№ k m
1 |
8 |
3 |
6 |
9 |
4 |
11 |
10 |
5 |
16 |
7 |
5 |
21 |
12 |
5 |
26 |
16 |
4 |
2 |
8 |
4 |
7 |
9 |
5 |
12 |
10 |
6 |
17 |
6 |
5 |
22 |
14 |
3 |
27 |
16 |
5 |
3 |
8 |
5 |
8 |
9 |
6 |
13 |
6 |
4 |
18 |
12 |
3 |
23 |
14 |
4 |
28 |
16 |
6 |
4 |
8 |
6 |
9 |
10 |
3 |
14 |
7 |
4 |
19 |
12 |
4 |
24 |
14 |
5 |
29 |
11 |
4 |
5 |
9 |
3 |
10 |
10 |
4 |
15 |
7 |
3 |
20 |
12 |
5 |
25 |
14 |
6 |
30 |
11 |
5 |
Пример 2.5. 10 книг, из которых четыре имеют красный переплет, наугад ставят на полку. В предположении, что все расстановки книг на полке равновозможны, найти вероятность того, что книги с красными переплетами окажутся стоящими подряд.
Решение. 10 книг можно на полке расставить n =10! способами. Для подсчета благоприятствующих комбинаций представим сначала, что красные книги связаны в одну пачку и переставляются как единая книга. Тогда переставить эту пачку и остальные шесть книг можно7! способами.
После того, как эта перестановка совершилась и красные книги оказались
стоящими подряд, развяжем пачку |
и |
на заданных четырех |
местах |
переставим красные книги между собой. Это можно сделать 4! способами. |
|||
По комбинаторному принципу |
всего |
благоприятствующих |
способов |
m = 4!×7!. Поэтому искомая вероятность равна (4!×7! ) / 10! =1 / 30. |
|
||
Ответ. 1/30.
Задача 2.5. Из n книг k1 имеют красные переплеты, а k2 –– синие. Книги наугад ставят на полку. Полагая равновозможными все расстановки книг, найдите вероятность того, что все красные книги будут стоять подряд и все синие тоже. (См. пример 2.5 и исходные данные.)
Исходные данные к задаче 2.5.
№ |
n |
k1 |
|
k2 |
№ |
n |
k1 |
k2 |
№ |
n |
k1 |
k2 |
№ |
n |
k1 |
k2 |
№ |
n |
k1 |
k2 |
|
||||
1 |
8 |
|
3 |
|
2 |
7 |
10 |
4 |
3 |
|
13 |
8 |
4 |
2 |
19 |
|
11 |
4 |
2 |
25 |
|
11 |
4 |
5 |
|
2 |
8 |
|
2 |
|
2 |
8 |
10 |
3 |
2 |
|
14 |
10 |
5 |
3 |
20 |
|
11 |
2 |
2 |
26 |
|
11 |
5 |
3 |
|
3 |
9 |
|
3 |
|
2 |
9 |
10 |
4 |
2 |
|
15 |
9 |
2 |
5 |
21 |
|
11 |
3 |
2 |
27 |
|
12 |
3 |
3 |
|
4 |
9 |
|
3 |
|
3 |
10 |
10 |
2 |
5 |
|
16 |
10 |
6 |
2 |
22 |
|
11 |
3 |
3 |
28 |
|
12 |
3 |
4 |
|
5 |
9 |
|
4 |
|
2 |
11 |
7 |
2 |
2 |
|
17 |
10 |
4 |
4 |
23 |
|
11 |
4 |
3 |
29 |
|
12 |
5 |
2 |
|
6 |
10 |
|
3 |
|
3 |
12 |
6 |
2 |
2 |
|
18 |
6 |
3 |
2 |
24 |
|
11 |
5 |
2 |
30 |
|
12 |
3 |
5 |
|
|
Замечание. |
Пусть n одинаковых предметов необходимо распределить |
|||||||||||||||||||||||
между k |
людьми. |
Это можно |
сделать Ck -1 |
= Cn |
способами. |
К |
такому |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+k -1 |
|
n+k -1 |
|
|
|
|
|
|
|
|
|
выводу приводят следующие соображения. |
Добавим к этимn предметам |
||||||||||||||||||||||||
k – 1 |
черный |
шар, поставим предметы и |
шары в один ряд, и будем их |
||||||||||||||||||||||
переставлять |
между |
собой. Число различимых перестановок будет равно |
|||||||||||||||||||||||
25