6. Производные простейших элементарных функций

Используя определение 4 производной, а также теоремы 6 и 7, можно доказать следующее утверждение.

Теорема 8. В области определения соответствующих функций имеют место формулы:

Таблица производных

1)

2)

3)

4)

5)

6)

7)

Докажем, например, формулу используя теорему 6 о производной обратной функции. Функцияявляется обратной по отношению к функциипричемпоэтому по теореме 6 имеем

И, наконец, рассмотрим пример вычисления производной сложной функции, состоящей из многих звеньев:

Лекция 3. Логарифмическая производная. Производные и дифференциалы высших порядков. Формула Тейлора с остаточными членами в форме Лагранжа и Пеано. Формулы Маклорена-Тейлора для простейших элементарных функций. Правило Лопиталя. Применение формулы Тейлора

1. Логарифмическая производная

При дифференцировании показательно-степенной функции обычно используютлогарифмическую производную Делается это так:

Например,

2. Производные и дифференциалы высших порядков

Производная есть сама функция отпоэтому можно взять от нее производную. Полученная таким образом функция (если она существует) называется второй производной от функциии обозначаетсяИ вообще:

если известна производная (порядка), то производнаяго порядка определяется так:При этом функцияназываетсяраз дифференцируемой в точке

Аналогично определяются дифференциалы высшего порядка. Именно:

если известен дифференциал порядка то дифференциалго порядка определяется так:при этом дифференциалнезависимой переменной и все его степенисчитаются постоянными дифференцирования.

Имеем И вообще, справедливо утверждение:если функция дифференцируемараз в точкето

Нетрудно доказать следующее утверждение.

Теорема 1. В области определения выписанных ниже функций справедливы равенства:

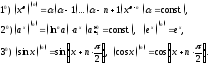
Производные 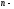порядка являются линейными операциями, т.е.

Производная порядка для произведениявычисляется довольно сложно.

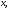Формула Лейбница. Если функции дифференцируемыраз в точкето имеет место равенство

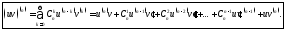
Здесь: число сочетаний изэлементов понулевая производная функциисовпадает с ней самой:Легко видеть, что формула (1) напоминает формулу бинома Ньютона; только в ней вместо произведения степеней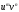стоит произведение производныхУчитывая это, легко записать, например, третью производную от произведения:

3. Формула Тейлора с остаточными членами в форме Пеано и Лагранжа

При вычислении пределов функций мы использовали таблицу 1 эквивалентных бесконечно малых. Например, при вычислении предела мы использовали формулыОднако этих формул не достаточно для вычисления предела

Нужны более точные формулы или так называемые асимптотические разложения высших порядков. Переходя к описанию таких разложений, введем следующее понятие.

Определение 5. Пусть функция 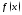определена в некоторой проколотой окрестности

точки Говорят, что функцияимеет в точке асимптотическое разложение го порядка,если существуют числа такие, что в некоторой в некоторой проколотой окрестности представляется в виде

Здесь Равенство (3) означает, что функцияаппроксимируется(приближенно равна) в некоторой малой окрестности точки многочленом. В каком случае функция имеет асимптотическое разложениепорядка? Ответ на этот вопрос содержится в следующем утверждении.

Теорема 2. Пусть функция 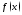имеет в точке производныедого порядка включительно. Тогда имеет в точке асимптотическое разложениепорядка вида

(формулу (4) называют формулой Тейлора с остаточным членом в форме Пеано или локальной формулой Тейлора).

Если в (4) положить то получим формулуназываемуюформулой Маклорена-Тейлора. Приведем формулы Маклорена-Тейлора для основных элементарных функций.

Теорема 3. Имеют место следующие разложения:

Доказательство этих формул базируется на подсчёте производной го порядка соответствующей функции. Докажем, например, формулу (2) .

Итак, пусть По теореме 1 имеем

Значит, в формуле

будут отсутствовать все четные степениа слагаемые с нечетными степенямиимеют видСледовательно имеет место формула 2.

Замечание 1. В формуле 2 остаточный член можно записать в видеа в формуле 3–

в виде (почему?).

Теорема 2 аппроксимирует функцию 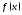лишь в достаточно малой окрестности точкиУсловия представления функциина некотором отрезке(гдеможет быть достаточно большим) по формуле Тейлора описаны в следующем утверждении.

Теорема 4. Пусть функция удовлетворяет следующим условиям:

1) существуют и непрерывны на отрезке ;

2) производная существует и конечна по-крайней мере на интервале

Тогда для всехфункция представляется в виде

где точка находится междуи

Формулу (5) называют (глобальной) формулой Тейлора с остаточным членом 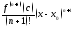в форме Лагранжа.

Если в формуле (5) положитьто получим равенствоили, обозначаябудем иметь

Эту формулу называют формулой Лагранжа.Она верна в случае,когда функция непрерывна отрезкеасуществует и конечна по-крайней мере на интервале