
- •1. Векторы. Координаты векторов и линейные операции над векторами
- •2. Скалярное, векторное и смешанное произведение векторов
- •1. Общее уравнение плоскости и уравнение в отрезках
- •2. Особые случаи расположения плоскости в пространстве
- •3. Условия параллельности и перпендикулярности плоскостей. Угол между двумя плоскостями
- •4. Решение различных задач на плоскость
- •5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •6. Прямая в пространстве
- •1. Матрицы и действия над ними. Матрицы специального вида
- •2. Определители матрицы и их свойства
- •3. Обратимость матриц. Вычисление обратной матрицы
- •4. Ранг матриц. Теорема о базисном миноре
- •1. Элементарные преобразования и приведение матриц к ступенчатому виду
- •2. Линейные системы алгебраических уравнений. Теорема Кронекера-Капеллил
- •3. Линейные пространства и базис. Структура общего решения однородной системы уравнений
- •4. Структура общего решения неоднородной системы уравнений. Алгоритм метода Гаусса построения общего решения линейной алгебраической системы уравнений
- •1. Линейные системы уравнений с квадратной матрицей. Правило Крамера
- •2. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
- •1.Изменение координат вектора и матрицы оператора при переходе к новому базису
- •2. Ядро и образ линейного оператора
- •3. Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов
- •Лекция 7. Евклидовы и метрические пространства. Неравенство Коши-Буняковского. Существование ортонормированного базиса
- •1. Евклидовы и метрические пространства
- •2. Ортогональные матрицы и ортогональные преобразования
- •2. Квадратичные формы. Приведение квадратичной формы к каноническому виду
- •3. Кривые второго порядка на плоскости
4. Структура общего решения неоднородной системы уравнений. Алгоритм метода Гаусса построения общего решения линейной алгебраической системы уравнений
Рассмотрим
неоднородную систему (1). Сначала заметим,
что разность
 двух ее решений будет решением
соответствующей однородной системы
двух ее решений будет решением
соответствующей однородной системы Действительно, имеем верные равенства
Действительно, имеем верные равенства и
и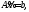 поэтому
поэтому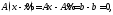 т.е. разность
т.е. разность является решением однородной системы
(2). Отсюда следует, что вектор
является решением однородной системы
(2). Отсюда следует, что вектор где
где фиксированное решение неоднородной
системы
фиксированное решение неоднородной
системы ,
а
,
а общее решение соответствующей однородной
системы
общее решение соответствующей однородной
системы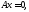 будет решением неоднородной системы
(1) при любых значениях постоянных
будет решением неоднородной системы
(1) при любых значениях постоянных Если
теперь
Если
теперь любое другое решение неоднородной
системы
любое другое решение неоднородной
системы ,
то его можно представить в виде
,
то его можно представить в виде Действительно, разность
Действительно, разность является решением однородной системы
является решением однородной системы а,
значит, по теореме 1 существуют постоянные
а,
значит, по теореме 1 существуют постоянные такие, что имеет место равенство
такие, что имеет место равенство
 ч.т.д.
Мы получили следующий результат.
ч.т.д.
Мы получили следующий результат.
Теорема
2. Общее
решение неоднородной системы
 имеет вид
имеет вид


где частное решение неоднородной системы
частное решение неоднородной системы ,
,
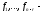 фундаментальная
система решений соответствующей
однородной системы
фундаментальная
система решений соответствующей
однородной системы
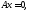 а
а
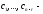 произвольные постоянные.
произвольные постоянные.
Теперь опишем алгоритм построения общего решения неоднородной системы (1).
Алгоритм метода Гаусса
1.
По системе (1) строим расширенную матрицу

2.
С помощью элементарных преобразований
строк приводим матрицу
 к ступенчатому виду
к ступенчатому виду
3.
По матрице
 восстанавливаем систему уравнений;
при этом уравнения, соответствующие
нулевым строкам матрицы
восстанавливаем систему уравнений;
при этом уравнения, соответствующие
нулевым строкам матрицы
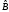 не выписываем.
не выписываем.
4. Неизвестные,
коэффициентами которых являются опорные
элементы матрицы
 объявляем
базисными (закрепленными), оставляем
их в левых частях уравнений, а остальные
неизвестные объявляем свободными и
переносим их в правые части уравнений.
объявляем
базисными (закрепленными), оставляем
их в левых частях уравнений, а остальные
неизвестные объявляем свободными и
переносим их в правые части уравнений.
5. Придавая свободным неизвестным значения произвольных постоянных, решаем полученную систему уравнений обратным ходом и находим базисные неизвестные и , наконец, записываем общее решение исходной системы уравнений в виде (4).
Пример 1. Найти общее решение системы уравнений


Решение.
Составляем
расширенную матрицу
 и приводим её к ступенчатому виду
и приводим её к ступенчатому виду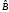 (опорные
элементы выделены в квадратиках):
(опорные
элементы выделены в квадратиках):

По
матрице
 восстанавливаем систему уравнений
(нулевую строку не учитываем):
восстанавливаем систему уравнений
(нулевую строку не учитываем):

Базисными
неизвестными являются
 и
и ;
оставляем их слева. Полагая значения
свободных неизвестных произвольными:
;
оставляем их слева. Полагая значения
свободных неизвестных произвольными: перенесём
их направо. Будем иметь
перенесём
их направо. Будем иметь

Теперь можно записать общее решение исходной системы (5):

Отсюда и из теоремы 2 следует, что

Найдены
частное решение
 системы (5) и ф.с.р. соответствующей
однородной системы.
системы (5) и ф.с.р. соответствующей
однородной системы.
Лекция 5. Правило Крамера. Линейное подпространство. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
В предыдущей лекции были рассмотрены общие системы линейных уравнений. В них число уравнений могло не совпадать с числом неизвестных. Соответствующая матрица системы была в общем случае прямоугольной. В случае систем с квадратной матрицей можно указать еще два способа решения (кроме изложенного выше метода Гаусса).
1. Линейные системы уравнений с квадратной матрицей. Правило Крамера
Итак,
рассмотрим систему
 линейных уравнений
линейных уравнений

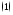
с
 неизвестными
неизвестными Матрица
Матрица этой системы квадратная, поэтому можно
вычислить ее определитель
этой системы квадратная, поэтому можно
вычислить ее определитель (называемыйглавным
определителем
системы (1)). Ниже будут участвовать и
другие определители, относящиеся к
системе (1). Введем их. Если в определителе
(называемыйглавным
определителем
системы (1)). Ниже будут участвовать и
другие определители, относящиеся к
системе (1). Введем их. Если в определителе
 выбросить
выбросить й
столбец и заменить его на столбец
й
столбец и заменить его на столбец свободных членов, то получим определитель
свободных членов, то получим определитель

называемый
 м
вспомогательным определителем
м
вспомогательным определителем
 Если определитель
Если определитель то для матрицы
то для матрицы существует обратная матрица
существует обратная матрица и эта матрица единственна. С помощью
неё можно решить систему (1). Действительно,
умножая обе части последнего равенства
(1) на
и эта матрица единственна. С помощью
неё можно решить систему (1). Действительно,
умножая обе части последнего равенства
(1) на будем
иметь
будем
иметь Мы доказали следующее утверждение.
Мы доказали следующее утверждение.
Теорема
1. Если
 то
система (1) имеет единственное решение
то
система (1) имеет единственное решение
Пример 1. Решить систему уравнений

Решение.Так как определитель то
данная система имеет единственное
решение
то
данная система имеет единственное
решение

Другой способ решения системы (1) основан на следующем утверждении.
Теорема
Крамера. Пусть
в системе (1) хотя бы один из
ее коэффициентов
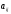 не равен нулю.
Тогда для того чтобы система (1) имела
единственноерешение,
необходимо и достаточно, чтобы её главный
определитель
не равен нулю.
Тогда для того чтобы система (1) имела
единственноерешение,
необходимо и достаточно, чтобы её главный
определитель
 был не равен нулю. В этом случае решение
системы (1) даётся формулами Крамера:
был не равен нулю. В этом случае решение
системы (1) даётся формулами Крамера:



Если
 и хотя бы один из определителей
и хотя бы один из определителей то система (1) решений не имеет. Если все
то система (1) решений не имеет. Если все ,
то система (1) либо не имеет решений
вообще, либо имеет их бесчисленное
множество.
,
то система (1) либо не имеет решений
вообще, либо имеет их бесчисленное
множество.
Доказательство проведем в случае для системы
для системы


с двумя
неизвестными
 Не умаляя общности, можно считать, что
Не умаляя общности, можно считать, что Из первого уравнения (3) находим
Из первого уравнения (3) находим
 и подставляем во второе уравнение; будем
иметь
и подставляем во второе уравнение; будем
иметь

Пусть
теперь
 тогда
тогда ,
поэтому
,
поэтому

Мы
показали, что в случае
 исходная система (3) равносильна системе
двух уравнений
исходная система (3) равносильна системе
двух уравнений поэтому если
поэтому если то система (3) имеет единственное решение
то система (3) имеет единственное решение
 Теорема доказана.
Теорема доказана.
Геометрическая
интерпретация теоремы Крамера. Уравнения
(3) есть уравнения прямых на плоскости Если
Если то коэффициенты указанных прямых не
пропорциональны, значит, эти прямые не
параллельны (см. Р.7), и поэтому пересекаются
в одной точке (в точке
то коэффициенты указанных прямых не
пропорциональны, значит, эти прямые не
параллельны (см. Р.7), и поэтому пересекаются
в одной точке (в точке ).
Если
).
Если то коэффициенты прямых (3) пропорциональны,
т.е.
то коэффициенты прямых (3) пропорциональны,
т.е. В этом случае система (3) равносильна
одному уравнению
В этом случае система (3) равносильна
одному уравнению которое
имеет бесчисленное множество решений
которое
имеет бесчисленное множество решений где
где произвольная постоянная, т.е. все точки
прямой
произвольная постоянная, т.е. все точки
прямой (см. Р.8) являются решениями системы (3).
И, наконец, если
(см. Р.8) являются решениями системы (3).
И, наконец, если и хотя бы один из определителей
и хотя бы один из определителей не равен нулю, то прямые (3) паралельны,
а, значит, система (3) не имеет решений
(см. Р.9).
не равен нулю, то прямые (3) паралельны,
а, значит, система (3) не имеет решений
(см. Р.9).
Пример 2. Решить систему уравнений

Решение. Вычисляем определители

По
теореме Крамера эта система либо имеет
бесчисленное множество решений, либо
не имеет их вообще. В нашем случае
 поэтому первое и третье уравнения
принимают вид
поэтому первое и третье уравнения
принимают вид
 Ни при каких
Ни при каких и
и эти равенства одновременно не выполняются,
значит данная система решений не имеет.
эти равенства одновременно не выполняются,
значит данная система решений не имеет.
