3. Кривые второго порядка на плоскости

Множество точек на плоскости⁶удовлетворяющих уравнению

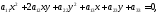
где не обращаются одновременно в нуль, называется кривой второго порядка на плоскости. Старшие члены в (2) образуют действительную квадратичную форму

с матрицей По теореме 4 ортогональным преобразованием(гдематрица из ортонормированных собственных векторовматрицы

) ее можно привести к каноническому виду , гдесобственные значения матрицыПри этом преобразовании исходное уравнение (2) приводится к виду

Так как то числоявляется определителем квадратичной формыПроведем классификацию кривых второго порядка (2) в случаеВ этом случае ( применяя метод выделения полного квадрата) уравнение (4) можно привести к видуСделав ещё одну замену переменныхполучим уравнение

если иесли

1Полезно запомнить, что в первый индекс номер строка, а номер столбца, на пересечении которых находится элемент

2Взаимно однозначное соответствие между двумя множествами, сохраняющее линейные операции между ними, называетсялинейным изоморфизмом этих множеств.

3Если оператор линейный, то пишутопуская скобки.

4В качестве обычно берут множество действительных чисел или множество комплексных чисел

5Приведение квадратичной формы к виду (1) называют ещёприведением её к главным осям

6Эту плоскость мы будем обозначать так же, как и множество геометрических векторов, буквой .

62