2. Ортогональные матрицы и ортогональные преобразования

Матрица (-й столбец) называется ортогональной, если ее столбцы образуют ортонормированную систему, т.е.

Например, матрица является ортогональной.

Теорема 3. Для того чтобы матрица была ортогональной, необходимо и достаточно, чтобы

Следствие 1. Ортогональная матрица обладает следующими свойствами:

1) 2)матрицы 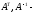ортогональные. Произведение двух ортогональных матриц есть ортогональная матрица. Матрица перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной матрицей.

Определение 6. Линейное преобразование (оператор) называется ортогональным, если в некотором ортонормированном базисе пространстваего матрица являетсяортогональной.

Теорема 3. Имеют место следующие свойства ортогональных преобразований:

1. Преобразование ортогонально тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный.

2. Ортогональное преобразование не изменяет скалярного преобразования, т.е.

3. При ортогональном преобразовании не изменяется длина (норма) вектора, а так же угол между векторами, т.е.

4. Произведение двух ортогональных преобразований есть ортогональное преобразование.

2. Квадратичные формы. Приведение квадратичной формы к каноническому виду

Квадратичной формой действительных переменных называется выражение вида

где числа (коэффициенты квадратичной формы). При этом матрицаназываетсяматрицей квадратичной формы (заметим, что она является симметрической: Используя эту матрицу, можно записать квадратичную форму кратко так:гдевектор-столбец. Определитель матрицыи её ранг называются соответственноопределителем и рангом квадратичной формы.

Посмотрим, как преобразуется квадратичная форма при линейном преобразовании. Пусть дана квадратичная форма . Сделаем в ней преобразованиебудем иметь

Если матрицаявляется невырожденной, то матрицыиназываютсяконгруэнтыми. Так же называются и соответствующие квадратичные квадратичные формы. Нетрудно показать, что определителиконгруэнтных матриц имеют одинаковые знаки, а сами конгруэнтные матрицы имеют одинаковые ранги.

Теорема 4. Любую действительную квадратичную форму ортогональным линейным преобразованием можно привести к каноническому виду

При этом собственные значения матрицыстолбцыматрицыявляются собственными векторами матрицысоответствующими этим собственным значениям, причем они образуют ортонормированный базис в пространстве

Теорема 5. Любую действительную квадратичную формуможно линейным невырожденным преобразованием привестик нормальному виду⁵

где ранг квадратичной формы. При этом число положительных и число отрицательных

квадратов в (1) не зависит от выбора преобразования (закон инерции квадратичных форм).

Следствие 2. Любая действительная симметрическая матрица ортогонально-подобна диагональной матрице, т.е.гдеортогональная матрица,При этомспектр матрицыа столбцыявляются собственными векторами матрицы

Заметим, что канонический и нормальный вид квадратичной формы определяются неоднозначно. Однако число положительных и число отрицательных квадратов во всех видах остаются неизменными (закон инерции квадратичных форм).

Пример 1. Привести к каноническому и нормальному виду квадратичную форму

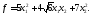
Решение. Квадратичную форму можно записать в виде

Находим собственные значения матрицы

Вычисляем собственные векторы матрицы для чего решаем системуприПолучим собственные векторы

образующие базис вОн является ортогональным базисом вно не ортонормированным. Нормируем собственные векторы, поделив их на их длины:

Теперь преобразующая матрица и ее обратная имеют вид

Следовательно, преобразование приводит исходную квадратичную форму к каноническому виду. Сделав еще одно преобразованиеприведем квадратичную форму к нормальному виду

Дадим еще один способ приведения квадратичной формы к нормальному виду, называемый методом Лагранжа.Продемонстрируем его на том же примере Назовемглавной переменнойту, которая входит в квадратичную форму в квадрате и в первой степени.

Это переменная Выделяем по ней полный квадрат:

Делаем замены переменных:Будем иметьЭто и есть нормальный вид квадратичной формы. Чтобы найти преобразованиеприводящее квадратичную формук нормальной форме, найдем обратную замену переменных:

Следовательно, матрица преобразования к нормальному виду будет такой:

Действительно, .