27 Туннельный эффект. Линейный гармонический осциллятор.
(туннелирование)
- квантовый переход системы через
область движения, запрещённую классич.
механикой. Типичный пример такого
процесса- прохождение частицы через
потенциальный барьер, когда её энергия
меньше высоты барьера. Импульс частицы
р в этом случае, определяемый из
соотношения
где
U(x)- потенц. энергия частицы ( т - масса),
был бы в области внутри барьера,
мнимой величиной.
В квантовой механике благодаря
неопределённостей соотношению между
импульсом и координатой подбарьерное
движение оказывается возможным. Волновая
ф-ция частицы в этой области экспоненциально
затухает, и в квазиклассич. случае) её
амплитуда в точке выхода из-под барьера
мала. Одна
из постановок задач о прохождении
потенц. барьера соответствует случаю,
когда на барьер падает стационарный
поток частиц и требуется найти величину
прошедшего потока. Для таких задач
вводится коэф. прозрачности барьера
(коэф. туннельного перехода) D, равный
отношению интенсивностей прошедшего
и падающего потоков. Из обратимости по
времени следует, что коэф. прозрачности
для переходов в "прямом" и обратном
направлениях одинаковы. В одномерном
случае коэф. прозрачности может быть
записан в виде
для
прямоугольного потенциального барьера:
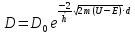
Из уравнения видно, что чем больше ширина и высота, и чем массивнее частица, тем меньше прозрачность. Явление прохождения частицы сквозь потенциальный барьер называется туннельным эффектом. Прохождение частицы сквозь барьер происходит без потерь энергии.
Гармонический асцилятор – система совершающая движение под действием квазеупругой силы.
Для
асцилятора:
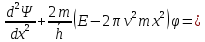решение однозначное, конечное и
непрерывное.
Уровни
на одном расстоянии, Еmin=1/2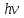
28 Основное состояние атома водорода по Шредингеру. Энергия основного cостояния. Размеры атома водорода.
Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не+, двукратно ионизованного лития Li++ и др.) сводится к задаче о движении электрона в кулоновском поле ядра.
Потенциальная
энергия взаимодействия электрона с
ядром, обладающим зарядом Ze (для атома
водорода Z = 1)
где r — расстояние
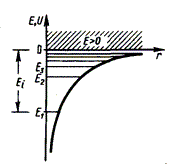
между электроном и ядром. Графически
функция U(r) изображена жирной кривой
на рис. U(r) с уменьшением r (при приближении
электрона к ядру) неограниченно убывает.
Состояние
электрона в атоме водорода описывается
волновой функцией y, удовлетворяющей
стационарному уравнению Шредингера,
учитывающему значение
где
т — масса электрона, Е — полная энергия
электрона в атоме. Так как поле, в котором
движется электрон, является
центрально-симметричным, то для решения
уравнения обычно используют сферическую
систему координат: r, q, j. Не вдаваясь в
математическое решение этой задачи,
ограничимся рассмотрением важнейших
результатов, которые из него следуют,
пояснив их физический смысл.
Энергия
молекулы водорода состоит из удвоенной
энергии атома водорода, энергии
кулоновского отталкивания между ядрами
и членов, определяющих взаимодействие
электронов между собой и с другим ядром.
В зависимости от спинового состояния
в формуле для
следует выбирать знак «+» или знак «-».
Знак «+» отвечает синглетному состоянию,
знак «-» — триплетному.
Величина Q(R)— это средняя энергия кулоновского взаимодействия между двумя электронами и электронов с «чужим ядром». Величина A(R) определяет вклад в энергию обменного взаимодействия, которая не имеет аналога в классической механике. Именно этот член определяет существенное различие между синглетными и триплетными состояниями.
Зависимость энергии основного состояния от расстояния между ядрами
Ковалентная
связь. Обменный интеграл для молеклы
водорода в определённом диапазоне
расстояний между атомами отрицательный.
Вследствие этого, для синглетных
состояний он обеспечивает дополнительное
притягивание между ядрами атомов, а
для триплетных — дополнительное
отталкивание. Дополнительное притягивание
обусловливает появление минимума
электронной энергии на расстоянии
приблизительно в 1,5 радиуса Бора (что
соответствует приблизительно 75 пм).
Этот минимум возникает только для
синглетного состояния, то есть для
антипараллельных спинов. Таким образом
устанавливается ковалентная связь
между атомами. Электроны двух атомов
водорода «спариваются».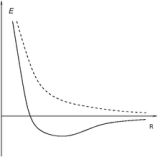
Насыщение ковалентной связи. Для параллельных спинов, то есть для триплетного состояния, дополнительный положительный вклад в энергию приводит к тому, что атому отталкиваются на любом расстоянии. Этим объясняется насыщение ковалентной связи. Молекула водорода может состоять только из двух атомов. Третий атом водорода не может образовать связь с молекулой потому, что его спин непременно будет параллельным одному из спинов электронов в составе молекулы. Параллельность спинов приводит к отталкиванию между ядрами на любом расстоянии.
Необходимо отметить, что на больших расстояниях между атомами они притягиваются в любых состояниях благодаря Ван-дер-Ваальсовому взаимодействию, которое, однако, намного слабее ковалентной связи. Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Радиус атома водорода 0.53 10-8 см
Масса атома водорода 1.67 10-27 кг