Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

примеры решения задач

.doc

Скачиваний:

Добавлен:

31.03.2015

Размер:

745.47 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

РЕШЕНИЕ ЗАДАЧ ПО ВМ-2 К ЭКЗАМЕНУ.

1. дифференц. в точке ?

Решение:

Аналогично

функция не является дифференцирумой в точке .

2. Найти сумму ряда:

Дело в том, что в книжках разобран вариант ряда номер 2). От варианта номер 1) он отличается только тем, что суммирование ведется с . Если же , то следует воспользоваться моим решением: (но не факт, что оно правильное).

1). Если ряд такой:

Решение:

Произведем замену переменной:

Найдем сумму ряда . Рассмотрим производную . Сумма убывающей геометрической прогрессии. Произведем обратные преобразования для нахождения суммы ряда , то есть возьмем интерграл.

Чтобы найти константу , найдем значение ряда в некоторой фиксированной точке

. Таким образом, сумма ряда:

при . И не существует при всех остальных x.

2). Если ряд такой: .

Решение:

Произведем замену переменной:

Чтобы найти константу , найдем значение ряда в некоторой фиксированной точке

. Таким образом, сумма ряда:

при . И не существует при всех остальных x.

3. в .

Решение:

4. . Исследовать ряд на сходимость.

Решение:

Обозначим

Используем признак Даламбера:

Так как по признаку Даламбера ряд сходится, если для всех достаточно больших выполнено неравенство и расходится, когда , то исходный ряд сходится.

5. .

Решение:

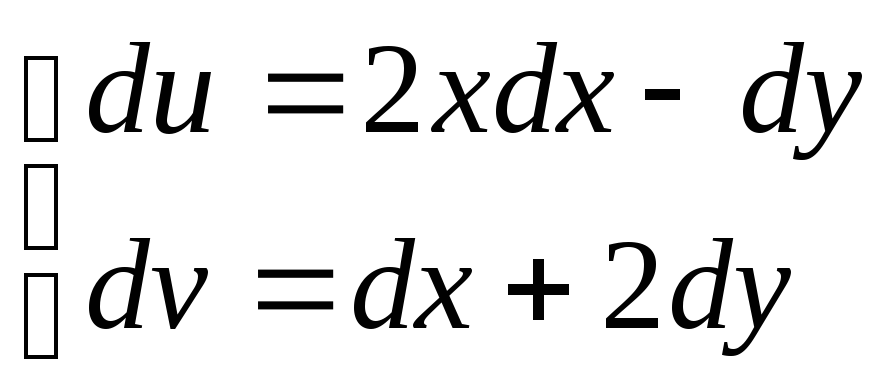
6. Исследовать на сходимость ряд:

Решение:

Воспользуемся предельным признаком сходимости:

Если два ряда и удовлетворяют условию , где - конечное число, не равное 0, то ряды и сходятся или расходятся одновременно.

Рассмотрим следующий ряд:

- это конечное число не равное нулю. Значит ряды и сходятся или расходятся одновременно.

Для исследования сходимости второго ряда используем интегральный признак сходимости рядов.

Если некоторая функция удовлетворяет условию , то если сходится, то и ряд сходится, а если расходится, то и ряд расходится.

Рассмотрим следующую функцию:

Интеграл сходится, значит и ряд сходится. А из сходимости этого ряда следует сходимость исходного.

Ряд сходится.

Решение:

Разложим этот ряд на сумму двух более простых рядов:

Найдем . Заметим, что есть производная от функции , умноженная на

Сумма ряда есть сумма убывающей геометрической прогрессии и поэтому равна , при условии, что . Тогда производная от такова:

Тогда при и не существует при

Ответ:

9. . Исследовать ряд на сходимость.

Решение:

Обозначим -й член этого ряда :

Найдем

Тогда ряд сходится по признаку Лейбница (по крайней мере условно).

10.

Доказать, что в точке

Решение:

. Действительно и не являются непрерывными в точке .

. Эта функция не является непрерывной в точке

не выполняются 2-е условие теоремы о равенстве смешанных производных.

Теорема (о равенстве смешанных производных): Есть функция Пусть:

1) в некоторой окрестности точки частные производные .

2) непрерывны в точке .

11.

12.

13.

14. Исследовать ряд на сходимость:

Решение:

Воспользуемся признаком Лейбница:

Если ряд удовлетворяет условиям:

1). - монотонно убывающая, начиная с некоторого

2). , то ряд сходится.

Рассмотрим . Так как функции возрастают, то возрастает функция , а следовательно последовательность убывает.

Таким образом, ряд сходится по признаку Лейбница.

15. Выписать :

Решение:

Берем дифференциал от левой и правой частей:

Отсюда выражаем :

16. Исследовать ряд на сходимость.

Решение:

Воспользуемся признаком Коши:

Если , то ряд сходится.

Если , то ряд расходится.

Так как , то исходный ряд расходится.

17.

18. Исследовать ряд на сходимость:

Решение:

Обозначим

Используем радикальный признак Коши:

Так как по радикальному признаку Коши ряд сходится, если , то можно сделать вывод, что исходный ряд сходится.

19. Разложить до в .

Решение:

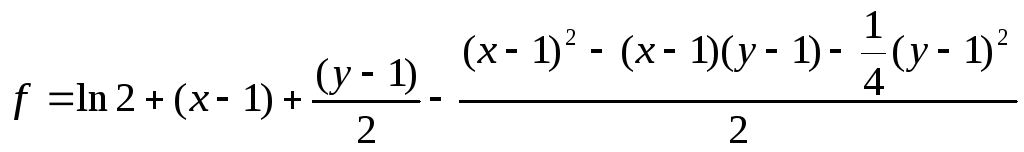20.

Найти экстремум:

Решение:

Пусть . Тогда:

. Возвращаясь к исходной переменной получим:

Отсюда получаем 4 точки:

1). 2) 3) 4)

Исследуем по очереди 4 точки:

1).

, . Не подходит по критерию Сильвестра.

2).

, . Не подходит по критерию Сильвестра.

3).

, . минимум в точке

4).

, . максимум в точке

21. Найти точки условного экстремума.

Решение:

- точки возможного условного экстремума.

условный минимум в точке .

22.

Решение:

23. Разложить в окрестности точки в ряд Тейлора.

Решение:

Корнями квадратного уравнения являются числа .

Если

24. Разложить функцию в ряд Тейлора по степеням x.

Решение:

Чтобы решить эту задачу, воспользуемся табличными разложениями в степенные ряды.

Воспользуемся разложением для

Этот ряд еще не является рядом Тейлора по степеням х. Воспользуемся табличным разложением еще раз. Преобразуем функцию:

. Воспользуемся табличным разложением для .

Пусть . Так как , то , . Из определения следует, что

. Теперь найдем все возможные комбинации , чтобы , где - произвольное фиксированное число, . Так как , то , то есть . Найдем коэффициент : так как раскладывается на сумму несколькими способами, то , где суммирование ведется по всем допустимым парам . Выразим индексы через :