ТИПОВЫЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ

ТИПОВЫЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ.

ВАРИАНТ 12.

Д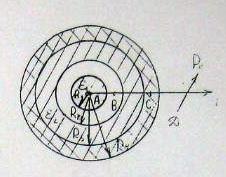линная коаксиальная цилиндричес­кая система образована цилиндрическим диэлектрическим стержнем (рис.1.). Радиус стерж­ня R₁ = 1 см, относительная диэлектрическая проницаемость ε₁ =1,5 , объемная плотность заряда ρ = – 1×10³ Кл∙м³. Металлическая труба имеет внутренний радиус (R₂ = 2 см) и наружный радиус (R₃ = 3 см). На единице длины трубы находится заряд τ= – 2×10⁶ Кл/м. Металлическая труба окружена цилиндрическим слоем диэлектрика радиу­сов R₃ = 3 см и R₄ = 4 см, относительная диэлектричес­кая проницаемость которого равна ε₂ =1,5 .

Необходимо:

1. Рассчитать напряженность электрического поля, электри­ческое смещение и электрический потенциал в точках А (r_А = 0,5 см), В (r_В = 1,5 см), С Рис. 1.

(r_С = 3,5 см) и D (r_D = 5 см). Принять начало отсчета потенциала на оси симметрии системы.

2. Построить графики E (r), D (r) и φ (r).

3. Найти поверхностную плотность связанных зарядов на границах диэлектриков.

4. Рассчитать энергию электрического поля заданной системы, приходящуюся на единицу длины в цилиндре радиуса r_D = 5 см.

5. Определить поверхностную плотность свободных зарядов на внутрен­ней и внешней поверхностях металлической трубы.

6. Рассчитать потенциальную энергию электрического диполя p_e = 1×10^-28 Кл∙м, находящегося в точке D и ориентированного под углом α=π к радиальному направлению. Определить момент сил, вращающих электрический диполь.

Решение:

1. Заметим, что точки, в которых требуется найти напряженности, электрические смещения и потенциалы электрического поля, лежат в четырех областях (рис. 2): область I (r_А < R₁), область II (R₁ < r_В < R₂), область III (R₃ < r_С < R₄) и область IV (r_D > R₄).

Для определения напряженности Е_А в области I проведем цилиндрическую поверхность S_А радиусом r_A и воспользуемся теоремой Остроградского — Гаусса. Так как внутри области I зарядов нет, то согласно указанной теореме получим равенство

, (1)

где Е_п — нормальная составляющая напряженности электрического поля.

И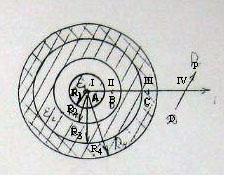з соображений симметрии нормальная составляющая Е_п должна быть равна самой напряженности и постоянна для всех точек коаксиального цилиндра, т. е. Е_п=Е_А=const. Поэтому ее можно вынести за знак интеграла. Равенство (1) примет вид

.

Так как площадь сферы не равна нулю, то E_А = 0, т. е. напряженность поля

Рис. 2. во всех точках, удовлетворяющих условию r_А < R₁, будет равна нулю.

Электрическое смещение D связано с напряженностью Е электрического поля соотношением

, (2)

где ε — диэлектрическая проницаемость среды; ε₀ — электрическая постоянная .

Так как, в области I E_А = 0, то из формулы (2) следует, что D_А = 0.

Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,

. (3)

Запишем связь между объемной плотностью заряда ρ и зарядом Q по следующей формуле:

, откуда . (4)

Здесь, V – объем, занимаемый зарядом; - площадь основания цилиндра.

Т.об., подставляя (4) в (3), получаем окончательную формулу для нахождения значения потенциала в точке А, т.е.

.

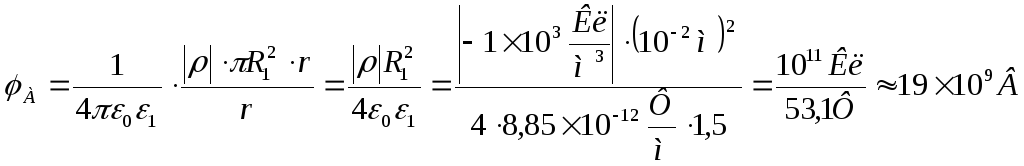В области II цилиндрическую поверхность проведем радиусом r_В. Так как внутри этой поверхности находится заряд Q₁ то для нее, согласно теореме Остроградского — Гаусса, можно записать равенство

. (5)

Так как Е_п = Е_B= const, то из условий симметрии следует

, или , откуда .

Подставив сюда выражение площади круга S₂, а также формулу (4), получим следующее выражение:

.

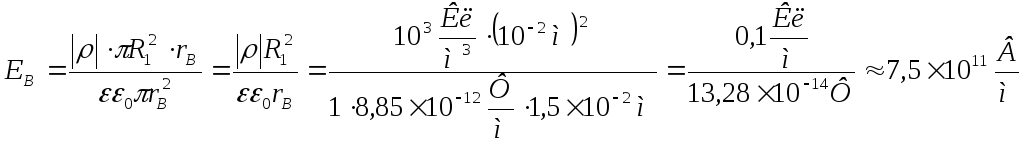Используя формулу (2), найдем значение электрического смещения в точке В

.

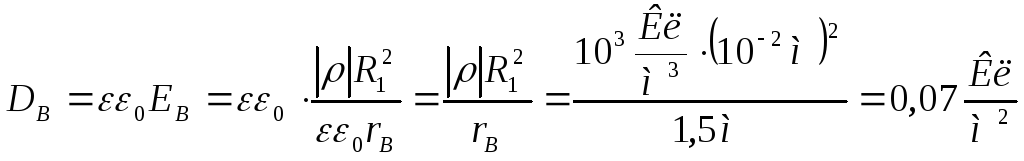Используя формулы (3) и (4), вычислим значение потенциала в области II.

.

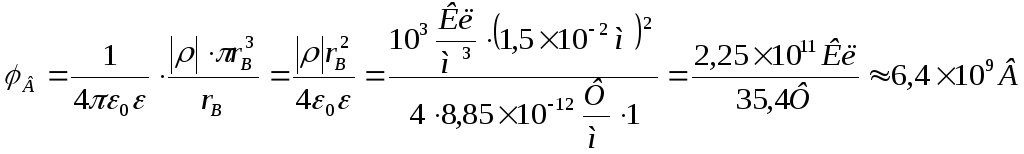В области III цилиндрическую поверхность проведем радиусом r_С. Эта поверхность охватывает суммарный заряд Q₁+Q₂. Следовательно, для нее уравнение, записанное на основе теоремы Остроградского — Гаусса, будет иметь вид

. (6)

Отсюда, использовав положения, примененные в первых двух случаях, найдем

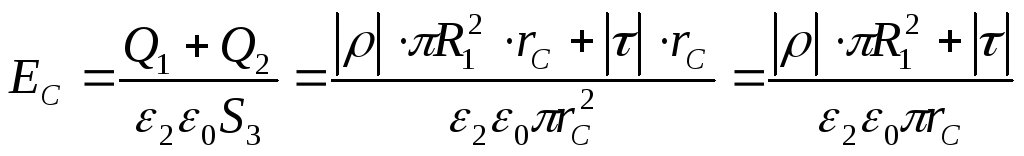. (7)

или .

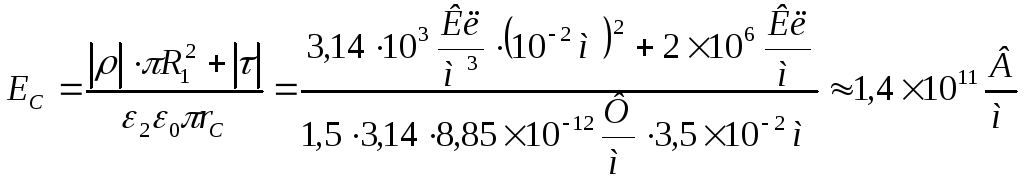Используя формулу (2), найдем значение электрического смещения в точке С

. (8)

Т.об., .

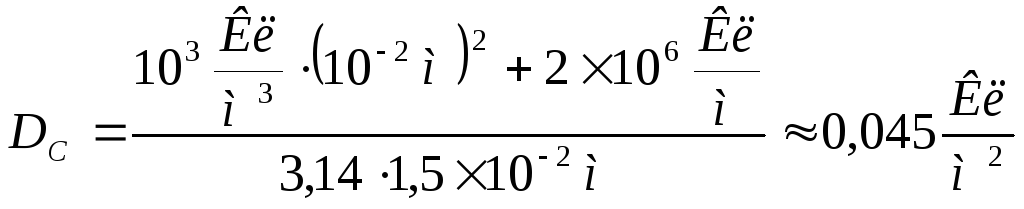Для нахождения потенциала в области III воспользуемся формулой (3) и формулой, нахождения заряда Q₂ через линейную плотность заряда τ, т.е.

, откуда . (9)

Используя формулы (3) и (9), вычислим значение потенциала в области III.

. (10)

или .

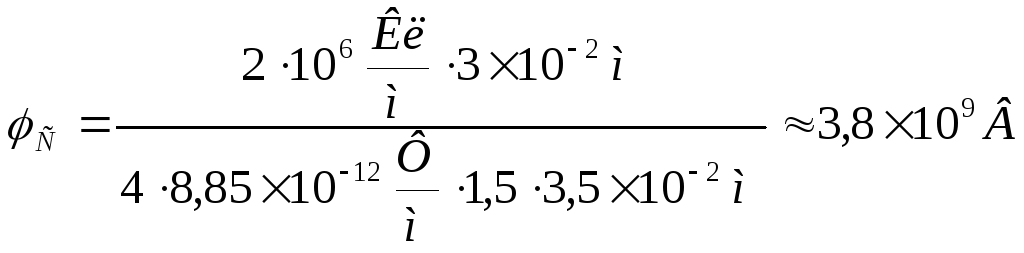В области IV цилиндрическую поверхность проведем радиусом r_D. Эта поверхность также охватывает суммарный заряд Q₁+Q₂. Следовательно, для нее уравнение, записанное на основе теоремы Остроградского — Гаусса, будет также иметь вид

.

Для нахождения значения Е_D в точке D, воспользуемся формулой (7) из предыдущего вычисления. Таким образом, получаем,

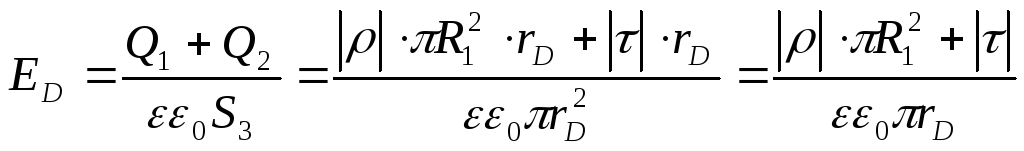
или .

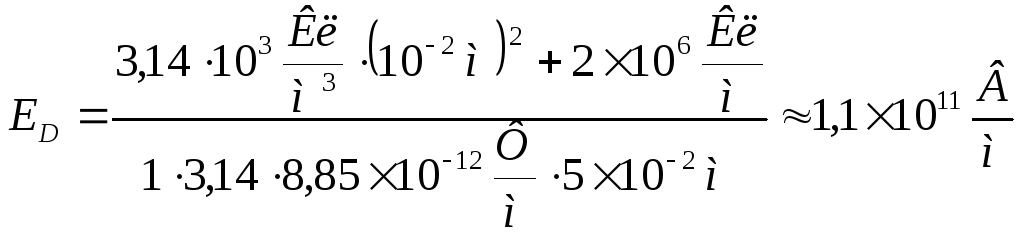Аналогичным образом, вычислим электрическое смещение D_D и потенциал φ_D в точке D области IV по формулам (8) и (10), т.е.

.

.

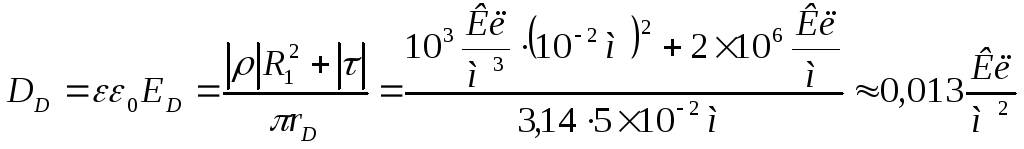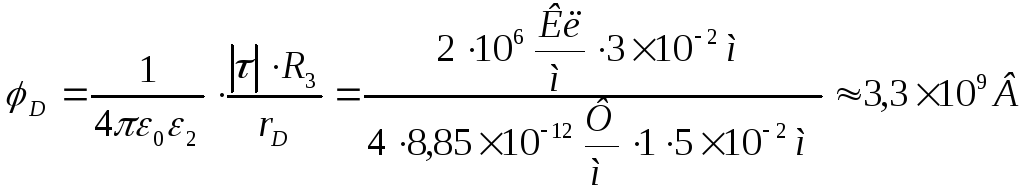2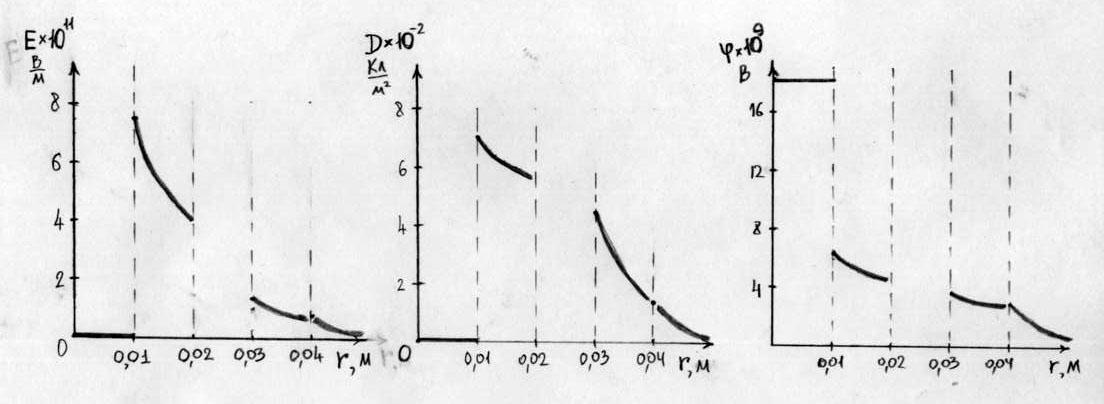. Графики зависимостей E (r), D (r) и φ (r) представлены на рисунках 3, 4, 5.

Рис. 3. Рис. 4. Рис. 5.

3. Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:

. (11)

В нашем случае сказано, что поверхностная плотность определяется в области III, где . Таким образом, формула (11) примет вид:

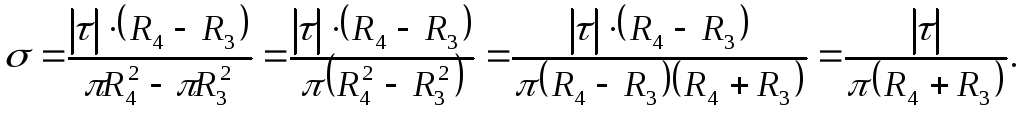(12)

Таким образом, получаем

.

4. Энергию электрического поля W_r заданной системы, приходящуюся на единицу длины в цилиндре радиуса r_D рассчитаем по следующей формуле:

, (13)

В области IV цилиндрическую поверхность охватывает суммарный заряд Q₁+Q₂. Следовательно, для нее уравнение (13), с учетом потенциала φ_D, запишется в следующем виде:

.

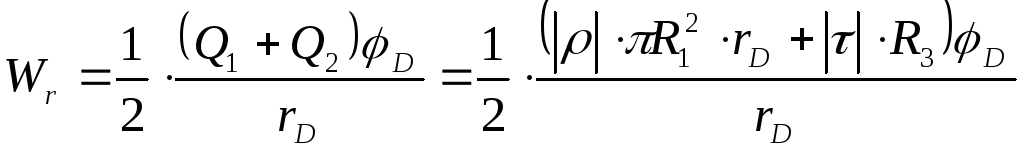Таким образом, получаем, .

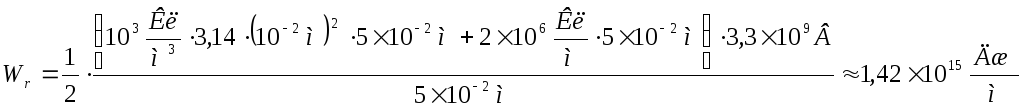5. Поверхностную плотность свободных зарядов на внутрен­ней (R₂ = 2 см) и внешней (R₃ = 3 см) поверхностях металлической трубы определим, воспользовавшись формулой (11). Учтем при этом, что заряд Q определяется по формуле (4). Тогда получаем, для внутренней поверхности:

.

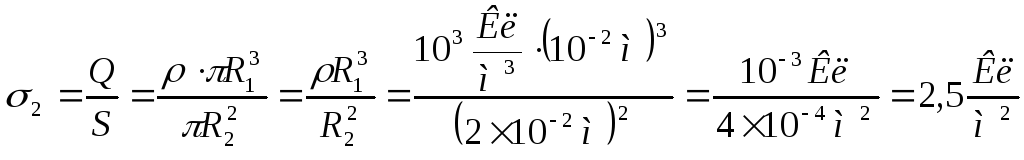Аналогично, и для внешней поверхности с радиусом R₃:

.

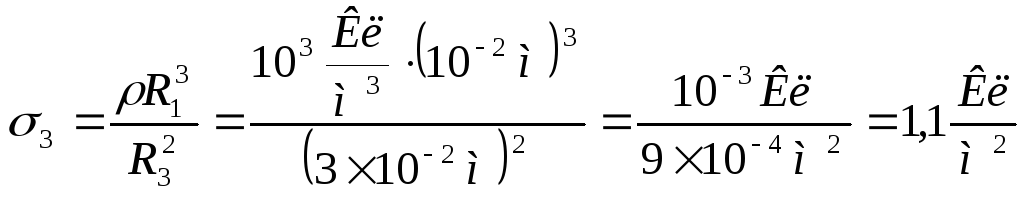6. Потенциальную энергию электрического диполя p_e = 1×10^-28 Кл∙м, находящегося в точке D и ориентированного под углом α=π к радиальному направлению определим по следующей формуле:

, (14)

где E = E_D – напряженность электрического поля, создаваемое зарядами нашей цилиндрической системой в точке D.

Т.об, получаем, .

Механический момент сил, действующий на диполь с электрическим моментом , помещенный в однородное электрическое поле с напряженностью , определяется по формуле:

или . (15)

Т.к. sinα = π = 0, то из формулы (15) следует, что М = 0.