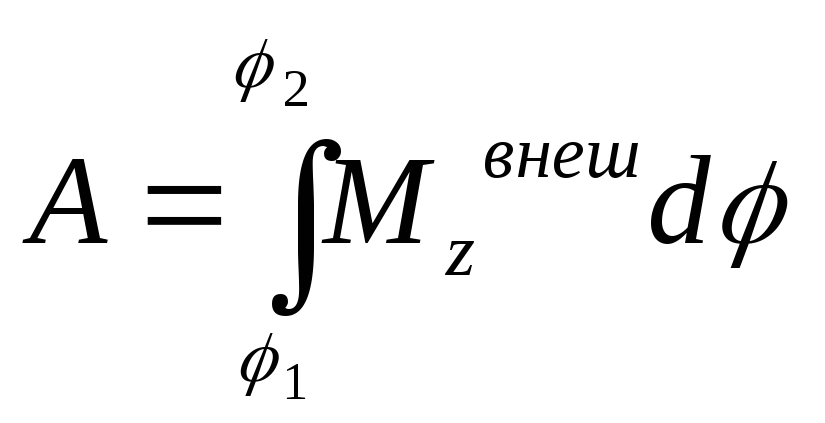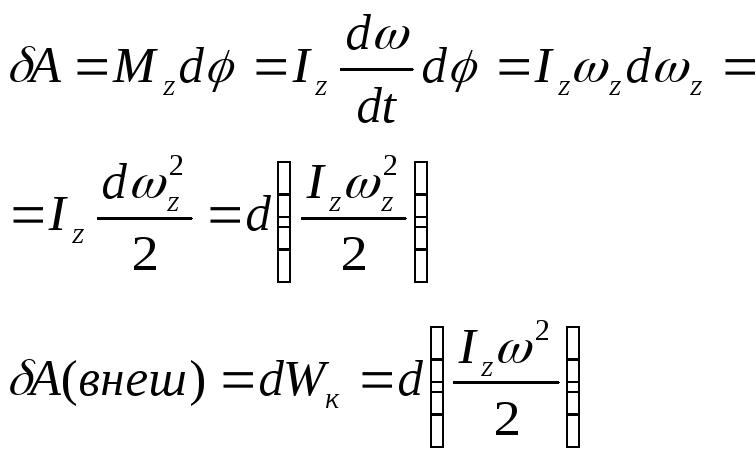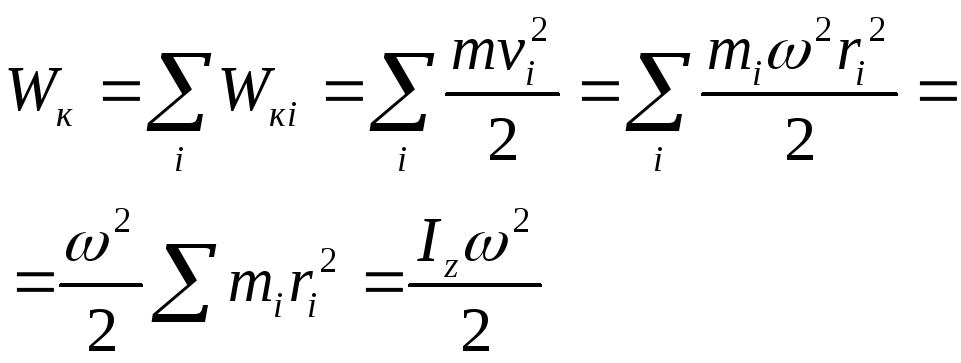Шпоргалка (механика-термодинамика)
.doc
|
1. Материальная точка. Абсолютно твердое тело. Тело отсчета. Система отсчета. Кинематический закон движения материальной точки. Вектор перемещения. Скорость и ускорение. Путь.
Материальной точкой называется физическое тело, размерами которого можно пренебречь в следующих условиях:
При поступательном движении любая прямая, проходящая через любые две точки тела, остается параллельной самой себе. В случае поступательного движения тела достаточно знать движение какой-либо одной из его точек, а само тело рассматривать как материальную точку.
Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого не изменяется при любом движении тела. Тело отсчета – это тело, относительно к-рого рассматривают положение других тел. Системой отсчета (СО) называется совокупность: - физического тела отсчета, - связанной с ним системы координат, - указание начала отсчета времени. Радиус-вектором точки в пространстве называется вектор, проведенный из начала координат в данную точку пространства. Траекторией данной точки тела называется множество точек пространства, проходимых этой точкой во время движения тела.
Для описания движения м. точки необходимо
задавать кинематический закон
движения, т.е. уравнение или систему
уравнения, определяющих положение
тела в любой момент времени относительно
выбранной с. отсчета. В случае векторного
способа задания положения точки в
пространстве кинематический закон
ее движения имеет вид
Перемещением называется векторная физическая величина, равная вектору, соединяющему начальное положение материальной точки с ее текущим положением. Перемещение материальной точки равно разности радиус-векторов этой точки, соответствующих текущему ее положению и ее начальному положению:
Путем называется скалярная физическая величина, равная длине дуги траектории, пройденной телом за заданное время.
Разобьем траекторию L
м. точки на бесконечно малые участки
длиной dL. Каждому участку
траектории dL будет
соответствовать перемещение
Ускорение характеризует быстроту изменения вектора скорости и определяется как производная скорости по времени:
|
2-3. Вектор ускорения. Нормальное и тангенциальное ускорение. Кинематический закон движения тела в случае постоянного ускорения. Границы применимости классического способа описания движения точки.
В общем случае направление вектора
ускорения тела неизвестно. Для его
нахождения выберем в каждой точке
траектории два единичных вектора
Проекция
Тангенциальное ускорение отвечает
за изменение скорости по величине:
Нормальное ускорение отвечает за изменение вектора скорости по направлению:
Равнопеременным движением называется движение с постоянным ускорением.
Законы изменения координат тела:
Все вышеизложенное относится к классическому способу описания движения м. точки. В случае неклассического рассмотрения движения микрочастиц понятия траектории их движения не существует, но можно говорить о вероятносит нахождения частицы в той или иной области пространства. Для микрочастицы нельзя одновременно указать точные значения координаты и скорости. В квантовой механике существует соотношение неопределенностей
В. Гайзенберга
|
4. Абсолютно твердое тело. Поступательное и вращательное движение абсолютно твердого тела. Кинематические характеристики вращательного движения (угловое перемещение, угловая скорость и угловое ускорение), связь их с линейными характеристиками движения точек тела.
Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого не изменяется при любом движении тела. Поступательным движением твердого тела называется такое движение, при котором все точки тела движутся одинаково. При поступательном движении любая прямая, проходящая через любые две точки тела, остается параллельной самой себе. В случае поступательного движения тела достаточно знать движение какой-либо одной из его точек, а само тело рассматривать как материальную точку. Вращательным движением абсолютно твердого тела наз. такое, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Рассмотрим
твердое тело, вращающееся вокруг
неподвижной оси. За бесконечно малый
промежуток времени dt
все точки тела повернутся на бесконечно
малый угол dφ. Будем
считать угол поворота вектором,
который направлен по оси вращения
тела в сторонв, определяемую правилом
правого винта (если правый винт вращать
по направлению вращения твердого тела
вокруг оси, совпадающей с осью вращения
тела, то напраление поступательного
движения винта дает направление
вектора угла поворота тела
Рассмотрим
поворот тела на малый угол
При
неравномерном вращении тела вводится
векторная величина, характеризующая
быстроту изменения угловой скорости,
наз. угловым ускорением:
Векторы
Если
твердое тело вращается относительно
оси, то каждая точка тела имеет
определенную линейную скорость
|
|
5. Динамика материальной точки. Масса. Сила. Импульс тела, импульс силы. Законы Ньютона. Динамика – это раздел физики, отвечающий на вопрос, почему так или иначе движется тело. Законы динамики были сформулированы Ньютоном в 1686г. Они являются обобщением опытных фактов, накопленных человеком в течение многих лет. Для того, чтобы сформулировать законы динамики, необходимо ввести ряд понятий. Сила определяется как физическая величина, служащая мерой воздействия на данное тело другого тела. Это векторная величина. Действие силы приводит:
Действие силы зависит:
Тело получает ускорение (изменяет скорость) под действием другого тела. В природе сущ. взаимодействие – действие тел друг на друга. Из опытов установили, что при вз-и двух тел:
То тело, к-рое при вз-и получает меньшее ускорение, т.е. меньше изменяет скорость, ближе к состоянию инерции, и оно более инертно.
В природе существует 4 типа вз-ий: 1) гравитационное 2) слабое 3) электромагнитное 4)сильное 2-й закон Ньютона. Из опыта стало известно, что при действии одной и той же силы на разные тела оказывается одинаковым произведение массы тела на его ускорение. Поэтому произведение массы тела на его ускорение принято за величину, выражающую силу.
Если на тело действует несколько сил, то ускорение тела равно векторной сумме ускорений, вызванных каждой силой в отдельности. А в результате оно будет таким, как будто бы его сообщила одна сила, заменяющая действие всех, ее называют равнодействующей, она равна векторной сумме сил, действующих на тело. Третий закон Ньютона: силы, с которыми две м. точки действуют друг на друга в ИСО, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.
Импульсом тела называется векторная физическая величина, равная произведению массы тела на его скорость:
В системе СИ за единицу измерения импульса - килограмм на метр в секунду (кгм/с) - принят импульс тела массой в 1 килограмм, движущегося со скоростью 1 метр в секунду.
Импульсом силы называется векторная
физическая величина, равная произведению
силы на интервал времени ее действия:
Импульсом системы сил называется векторная физическая величина, равная произведению векторной суммы этих сил (то есть равнодействующей этих сил) на интервал времени их действия: В системе СИ за единицу импульса силы - ньютон на секунду (Нс) или килограмм на метр в секунду (кгм/с) - принимается импульс силы величиной в 1 ньютон, которая действует в течение 1 секунды.
|
6. Система материальных точек. Центр масс системы материальных точек. Теорема о движении центра масс системы материальных точек.
Любое тело можно представить как совокупность материальных точек. Центром масс системы взаимодействующих материальных точек называется такая точка пространства, радиус-вектор которой определяется выражением:
Центра масс системы совпадает с ее центром тяжести, если поле сил тяжести в пределах данной системы тел можно считать однородным. Скорость центра масс:
Если скорость центра масс равна 0, то говорят, что система в целом покоится. Сама же скорость центра масс имеет смысл скорости движения всей системы как целого. Из последней формулы следует:
Подставим
эту формулу
где
Полученное выражение наз. уравнением движения центра масс системы тел. Согласно этому уравнению, центр масс любой системы тел движется так, как если бы вся масса системы была сосредоточена в этой точке, и к ней были бы приложены все внешние силы. Если центр масс системы движется равномерно и прямолинейно, то импульс системы сохраняется в процессе движения. Справедливо и обратное утверждение.
|
7. Система материальных точек. Внутренние и внешние силы. Импульс материальной точки и импульс системы материальных точек. Закон сохранения импульса. Условия его применимости.
Любое тело можно представить как совокупность материальных точек. Рассмотрим
систему N
м. точек массами
Запишем 2-й з-н Ньютона для каждой точки:
Сложив эти уравнения, получим
В
соответствии с 3-им законом Ньютона
Из
полученной формулы следует, что импульс
системы м. точек могут изменить только
внешние силы, если их геометрическая
сумма не равна 0. Система тел называется
замкнутой, если
на нее не действуют внешние силы или
действие этих сил взаимно компенсировано.
Импульс замкнутой системы взаимодействующих
тел не изменяется при любом движении
тел системы (Закон сохранения
импульса системы взаимодействующих
тел):
Строго говоря, закон сохранения импульса выполняется только для замкнутой системы Но если на систему не действуют ударные (импульсные) силы, то для малых интервалов времени можно с достаточной степенью точности считать, что импульс сохраняется. Например, в задачах на соударения и в задачах о взрывах импульсом ограниченной силы тяжести можно пренебречь Кроме того, сохраняется проекция импульса системы взаимодействующих тел на ту ось, вдоль которой внешние силы не действуют: Если в задаче, описывающей кратковременное взаимодействие тел, не задано время взаимодействия, то предполагается модель бесконечно малого времени взаимодействия
В этом случае можно учитывать лишь ударные (импульсные) силы. |
|
8.Основное уравнение динамики вращательного движения абсолютно твердого тела.
Вращательным движением абсолютно твердого тела наз. такое, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Рассмотрим вращение м. точки массой m вокруг некоторой оси по окружности радиусом R под действием силы F. Положение точки определяется радиусом-вектором r, проведенным из произвольного полюса О, лежащего на оси вращения. Векторное
произведение радиуса-вектора точки,
проведенного из полюса, на вектор силы
носит название момента силы
относительно полюса:
Модуль момента силы
h – плечо силы – длина перпендикуляра, опущенного из точки О на линию действия силы. Момент силы относительно полюса не меняется при переносе силы вдоль линии ее действия, поскольку при этом не меняется плечо силы. Момент равнодействующей нескольких сил равен сумме моментов каждой силы относительно полюса. Таким образом, основное уравнение динамики вращательного движения м. точки может быть записано в виде
Основное уравнение динамики вращательного движения системы материальных точек:
т.е. скорость изменения момента импульса системы м. точек равна суммарному моменту внешних сил, действующих на нее.
|
9.Момент инерции тела относительно оси. Расчёт моментов инерции тел простейшей формы. Момент инерции:
где индекс «z» указывает на выбранную ось. Иная форма записи основного уравнения динамики вращательного движения м. точки:
Момент инерции – мера инертности м. точки во вращательном движении, он определяет момент сил, который должен быть приложен к телу для придания ему определенного углового ускорения. Момент
инерции твердого тела – это сумма
моментов инерции отдельных м. точек,
его составляющих:
Момент инерции обладает свойством аддитивности, т.е. момент инерции системы точек равен сумме моментов инерции каждой точки в отдельности. Момент инерции зависит от выбора оси вращения системы. Кольцо
Диск,
цилиндр
Стержень
Шар
Сфера:
При
вычислении момента инерции тела,
вращающегося вокруг оси, не проходящей
через центр инерции , следует пользоваться
теоремой о параллельном
переносе осей,
или теоремой Штейнера основным
уравнением динамики поступательного
движения Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями.
|
10. Момент импульса точки, тела, системы тел. Закон сохранения момента импульса, условие его применимости. Пример.
Рассмотрим вращение м. точки массой m вокруг некоторой оси по окружности радиусом R под действием силы F.
Положение точки определяется радиусом-вектором r, проведенным из произвольного полюса О, лежащего на оси вращения. Векторное
произведение радиуса-вектора м. точки,
проведенного из полюса, на импульс
этой точки называется моментом
импульса м. точки относительно полюса: Моментом импульса системы точек относительно полюса наз. сумма моментов импульсов каждой м. точки системы относительно этого полюса:
Основное уравнение динамики вращательного движения системы материальных точек:
т.е. скорость изменения момента импульса системы м. точек равна суммарному моменту внешних сил, действующих на нее. Если суммарный момент внешних сил, действующих на систему точек, равен 0, то момент импульса такой системы остается постоянным. Это – закон сохранения момента импульса. |
|
11.Закон сохранения импульса.
Вывод из формализма Ньютона
Р
П
г или
К (постоянный вектор).
То
есть суммарный импульс системы частиц
есть величина постоянная. Нетрудно
получить аналогичное выражение для
одной частицы.
Следует учесть, что вышеприведенные
рассуждения справедливы лишь
для замкнутой
системы.
Также стоит подчеркнуть, что
изменение импульса Закон сохранения импульса 1) Если сумма ПРОЕКЦИЙ внешних сил на какую-либо ось координат равна нулю, то сохраняется ПРОЕКЦИЯ полного импульса системы на эту ось. 2) Если в кратковременном процессе (например взрыв снаряда или соударение двух тел) возникающие внутренние силы ГОРАЗДО БОЛЬШЕ внешних (например силы, разрывающие снаряд, гораздо больше силы тяжести), то за время этого процесса изменением импульса МОЖНО ПРЕНЕБРЕЧЬ.
|
12.Кинетическая энергия материальной точки. Вращательное движение твердого тела. Кинетическая энергия тела, вращающегося относительно неподвижной оси. Работа при вращательном движении.
Пусть
материальная точка движется из
положения 1, где она имела скорость
Таким образом, доказана теорема об изменении кинетической энергии: изменение кин. энергии м. точки равно алгебраической сумме работ всех приложенных к ней сил.
Вращательным движением абсолютно твердого тела наз. такое, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Если
рассматривать абсолютно твердое тело
как систему м. точек, то поскольку
внутренние силы работы не совершают,
то работа, совершаемая внешними силами
при повороте тела относительно оси
z:
|
13.Кинетическая энергия сложного движения. Теорема Кёнинга. Теорема об изменении кинетической энергии.
Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.
Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс: Ек=Ек+Еi Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.
Выразим
относительную кинетическую
энергию Tr системы S как
энергию, вычисленной относительно
подвижной системы
координат.
Пусть
Е
Теорема
об изменении кинетической энергии
доказанная для точки будет справедлива
для любой точки системы
Подчеркнем,
что внутренние силы не исключаются.
Для неизменяемой системы сумма работ
всех внутренних сил равна нулю и
Если связи, наложенные на систему, не изменяются со временем, то силы, как внешние так и внутренние, можно разделить на активные и реакции связей, и уравнение теперь можно записать:
В динамике вводится такое понятие как "идеальная" механическая система. Это такая система, наличие связей у которой не влияет на изменение кинетической энергии, то есть
Такие связи, не изменяющиеся со временем и сумма работ которых на элементарном перемещении равна нулю, называются идеальными, и уравнение (19.2.5) запишется:
|


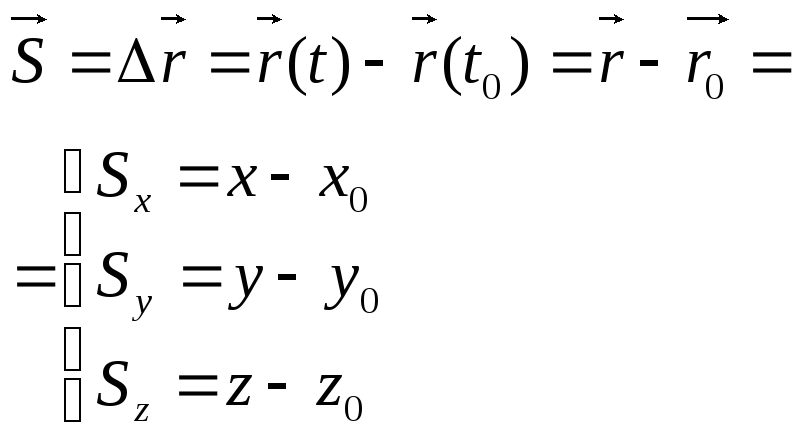
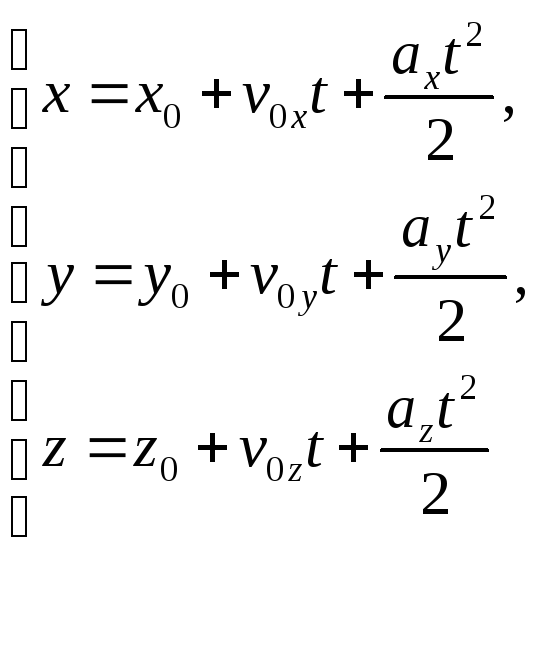
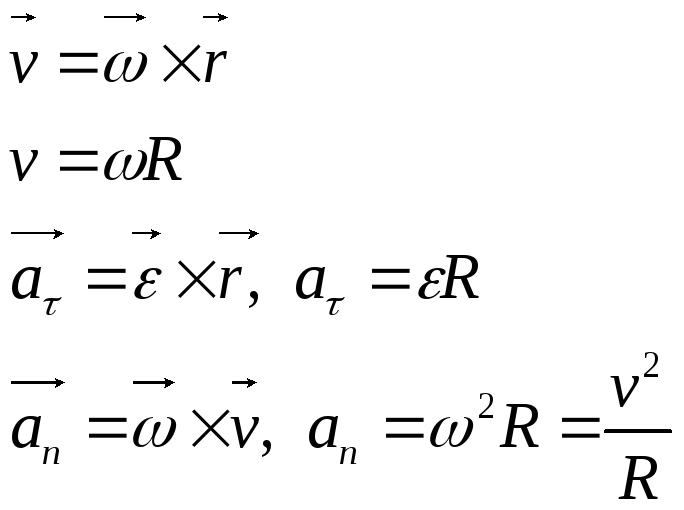
 где
где
 Величина
Величина
 А
– работа сил, приложенных к материальной
точке при вращении.
А
– работа сил, приложенных к материальной
точке при вращении.