Угловая скорость подвижного трехгранника, относительно другого трехгранника

- неподвижный трехгранник. .

- жестко связ с АТТ.

- единичные вектора .

. Рассмотрим разложение вектора по векторам:

,

Существуют три независимых коэффициента разложения векторов по векторам. Введем следующие обозначения:

(1)

Определение вектора угловой скорости подвижного трехгранника на оси этого подвижного трехгранника.

(2)

Вектор угловой скорости трехгранника относительнохарактеризует изменение положения подвижного трехгранника.

(3)

(3)

Аналогично: (3)

БИЛЕТ 7.

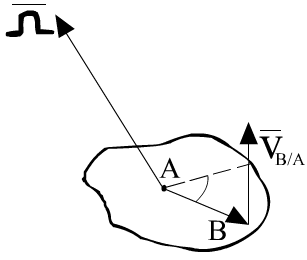, где- скорость движения в точке В относительно точки А

Существует такой вектор - угловая скорость АТТ.

Определение вектора угловой скорости подвижного трехгранника на оси этого подвижного трехгранника.

(2)

Вектор угловой скорости трехгранника относительнохарактеризует изменение положения подвижного трехгранника.

(3)

(3)

Аналогично: (3)

Определение: угловой скоростью АТТ будем называть угловую скорость подвижного трехгранника, жестко связанного с АТТ.

Корректно ли такое определение?

Угловая скорость тела не зависит от выбора начала координат или полюса.

.

В подвижном трехграннике проекции не изменяются.

, А- полюс. .

Пусть С- произвольная точка АТТ.

.

.

- угловая скорость для точки А., - угловая скорость для точки В.

= =+

=

Таким образом, доказана теорема о независимости угловой скорости от выбора полюса.

Где бы ни находилось начало трехгранника, угловая скорость остается одной и той же.

- формула Эйлера для связи скоростей двух точек АТТ.

БИЛЕТ 8.

Пусть - неподвижная система координат. Точки А и В принадлежат АТТ.

,

, так как (из определения АТТ).

Точка В относительно точки А движется по окружности постоянного радиуса.

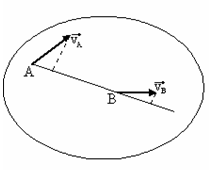
Теорема (о проекциях скоростей на прямую, их соединяющую).

Проекции скоростей двух точек твёрдого тела на прямую, их соединяющую равны между собой.

Доказательство.

=0, так как , что и требовалось доказать.

БИЛЕТ 9.

Проведем дифференцирование формулы Эйлера.

, , =- угловое ускорение АТТ,=.

- формула Ривальса.

где - тангенциальное ускорение,- осестремительное ускорение.

, прох. через В.

БИЛЕТ 10.

Поступательным движением АТТ называется такое движение АТТ, при котором любая прямая, проведённая в АТТ, остаётся параллельной своему начальному положению.

- подвижный трехгранник, связанный с АТТ. - единичные вектора подвижной системы координат, не меняющиеся по направлению, а также постоянные по длине.

, ,,траектории всех точек совпадают с точностью до параллельного переноса.

БИЛЕТ 11.

Вращающим движением а.т.т. относительно неподвижной оси называется

такое движение, когда в теле существует такие 2 т-ки, такие что

т. А движется по окружности, т.к. расстояние от точки О до А

Величина скорости точки = модулю расстояния угловой скорости

и расстояния до оси вращения.

Вектор скорости т. А

По формуле Ривальса:

Вторая составляющая ускорения называется осестремительным ускорением.

БИЛЕТ 12.

Плоско-параллельное движение АТТ.

Называется такое движение, при котором скорости всех точек АТТ параллельны некоторой неподвижной в пространстве плоскости.

Пример1. Безотрывное движение (скольжение) АТТ по неподвижной плоскости и скорости всех точек будут параллельны плоскости.

Пример 2. Качение цилиндра. Скорости всех точек цилиндра будут перпендикулярны образующим цилиндра.

Вращение вокруг неподвижной оси – частный случай плоско параллельного движения.

жестко связанос АТТ

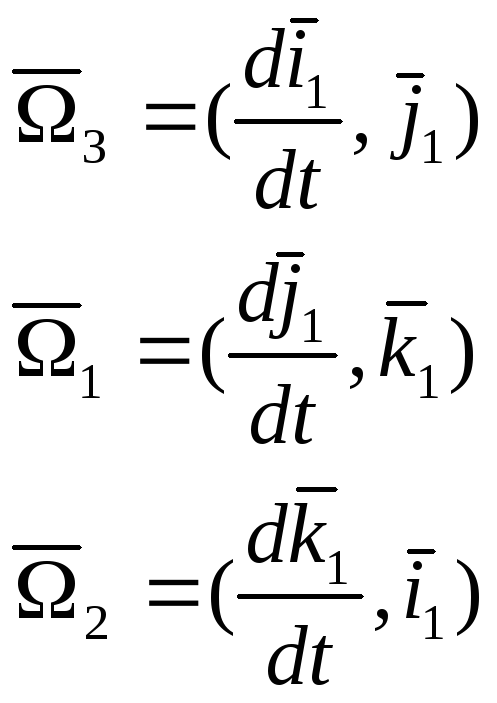
Аналогично:

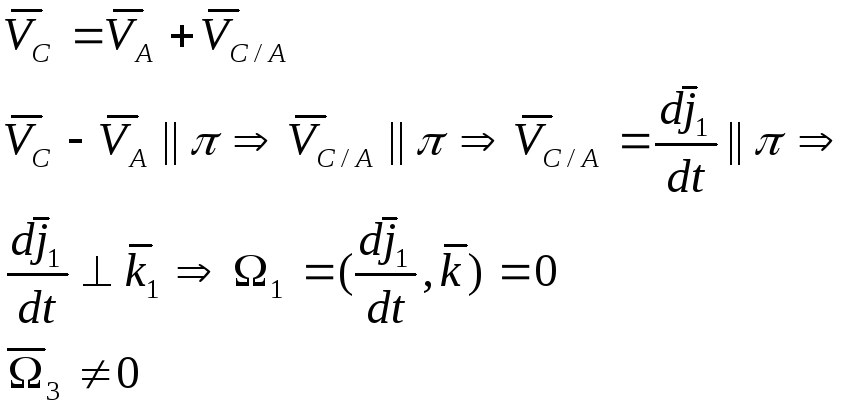
Угловая скорость АТТ перпендикулярна неподвижной плоскости.

Скорости всех точек, лежащих на одном перпендикуляре плоскости одинаковы.

Распределение скоростей в любом сечении плоскостью, || -ной плоскости -одинаковы

.

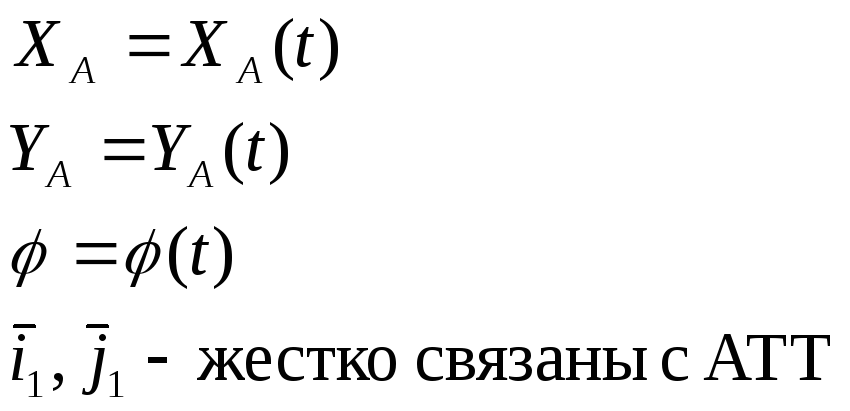
Эти уравнения определяют движение плоского сечения.

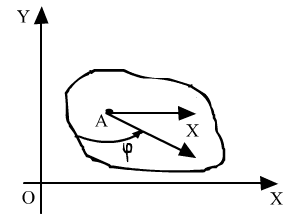
- неподв. трехгр-к.

Формула Эйлера:

- кинематический угол

Для нахождения кинематического угла следует в начало графа т.А поместить ось x, затем от оси х к отсчитать угол против часовой стрелки, тогда:

Для плоскопараллельного движения:

проекции на оси

,

БИЛЕТ 13.

Мгновенный центр скоростей плоского сечения.

МЦС плоского сечения называется такая точка, скорость в которой в данный момент времени = 0

Теорема:

Если угловая скорость плоского сечения отлично от нуля, то МЦС существует и он единственен.

Доказательство:

Пусть S-плоское сечение

направлен к нам

Пусть т.

а) А-МЦС

б)

Направление на выберем в соответствии с направлением вращения т.е. повернемна 90 против часовой стрелки.

Выберем

Но вектор и, принадлежащий сечению.

Согласно определению векторного произведения:

(по построению точки Р)=

Таким образом существование МЦС доказано.

Докажем теперь единственность. Пусть существует две точки P₁, P_{2 .}

Возьмем произвольную точку . Тогда по формуле Эйлера:

Значит точки P₁, P₂ совпадают. ч.т.д.

Понятие МЦС позволяет построить картину распределения векторов скоростей в плоском сечении.

Таким образом:

Вектор скорости любой точки плоского сечения перпендикулярен радиусу, проведенному из МЦС.

а) ,и так далее.

б) Скорость точки плоского сечения пропорциональна расстоянию т этой точки до МЦС

т.к.

Способы нахождения МЦС.