2. Учет влияния аддитивных составляющих параметров неидеальности оу.
К таким параметрам можно отнести:
,
,
,
,
.
Рассмотрим
схему при
(то есть собственный коэффициент
усиления ОУ равен
).
Чтобы
не вводить лишних параметров, примем,
что в
уже заложено собственное
и его изменение при изменении температуры,
то есть:
Аналогично:
(то
есть само
не учитываем, причину объясним позже).
приложено
к
,
так как ток идет так как показано на
рисунке, то есть
.
(заменяем
на эквивалентное).
(самостоятельно).
Фигурной скобкой отмечена абсолютная погрешность выходного напряжения.
-
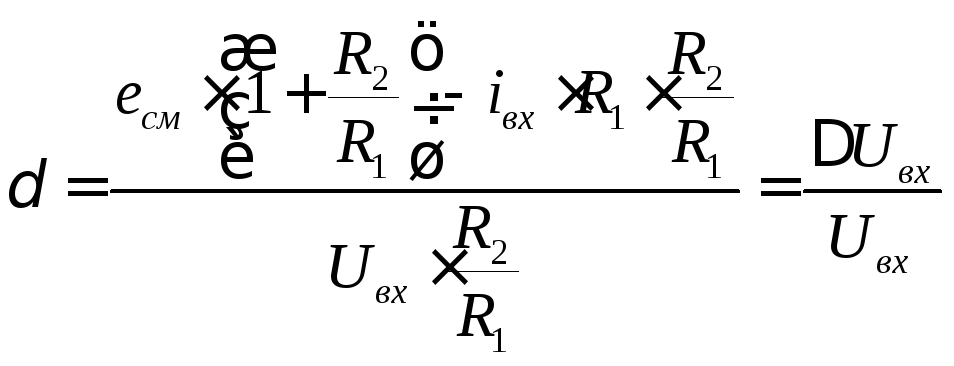относительная погрешность выходного
напряжения из-за изменения
и
.
Относительная
погрешность зависит от
:
чем больше
,
тем погрешность меньше:
К примеру:
А.
Ом.
Ом.
мВ.
В.
Если
В, то
.
Если
В, то
.
Энтропия
-
помеха составляет
от входного сигнала:
мВ.
Для
компенсации влияния входных токов
обычно применяется следующая схема,
где
:
Ток
течет по
,
изменяет параметры всего усилителя в
целом.
Схема замещения:
-
погрешность, определяемая разностью
входных токов. Она значительно меньше,
чем входной ток.
(погрешность
в 2-3 раза меньше, чем в предыдущем случае,
но она есть).
Численный пример.
А.
А.
Ом.
Ом.
(отсутствует
компенсация
)
(присутствует
компенсация
)
Способы компенсации напряжения смещения.
Нужно
вводить дополнительный потенциал на
один из входов, чтобы на выходе был ноль:
.
Простейшая схема:
потенциометр
напряжение
компенсации
Знак
неизвестен, мы не можем сказать какой
потенциал нужно подать: положительный
или отрицательный. Поэтому мы включаем
в схему потенциометр и, крутя его ручку,
добиваемся того, чтобы на выходе был
ноль.
Смысл компенсации:
«
»
в данном выражении означает, что мы не
знаем знак разности входных токов и
знак напряжения смещения.
Подобный
алгоритм позволяет компенсировать
,
,
разность входных токов.
Но
все равно остались параметры, которые
нам не удалось скомпенсировать. Это
и
.
Поэтому:
-
изменение температуры в процессе работы
устройства.
При
Ом.
Ом.
(до
микровольт).
Нам удалось повысить точность нашего преобразования.
Практическая схема балансировки нуля.
Данная схема хорошо балансирует. Само напряжение смещения- величина маленькая (порядка мВ). Маленькое изменение потенциометра вызывает большое изменение входного напряжения.
Благодаря сопротивлениям, мы можем хорошо балансировать ноль (маленьким изменением потенциометра).
,
где
.
Нам удалось снизить влияние аддитивных параметров, но не удалось их устранить вообще.
Самые худшие последствия от действия аддитивных параметров возникает при использовании интегратора:
Схема замещения:
.
Мы
будем всегда интегрировать
и
.
Поэтому это приведет к тому, что при
,
на выходе будет интегрировать напряжение:
Это процесс может происходить довольно долго, напряжение будет изменяться. Очень нестабильная картинка.
Рано или поздно мы «доинтегрируемся» до предела напряжения и интегратор не сможет больше интегрировать сигнал на входе. С этим бороться практически невозможно, хотя есть два способа: