Свойства скалярного произведения:

1°     - симметричность.

2°    . Обозначается  и называется скалярный квадрат.

3°    Если , то 

4°    Если  и  и , то . Верно и обратное утверждение.

5°    

6°    

7°    

Билет 17

екторным произведением ненулевых векторов  и  называется вектор , обозначаемый символом  или , длина которого (рис. 1).

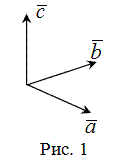
Свойства векторного произведения:

1°    , тогда и только тогда, когда 

2°    

3°    Модуль векторного произведения  равен площади параллелограмма, построенного на заданных векторах  и  (рис. 2), т.е.

4°    

5°    

Если векторы заданы своими координатами , , то векторное произведение находится по формуле:

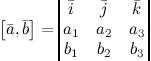
Смешанным произведением трех векторов , ,  называется число, равное скалярному произведению вектора  на вектор : 

Свойства смешанного произведения:

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда . Если же , то векторы ,  и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Если векторы ,  и  заданы своими координатами, то их смешанное произведение вычисляется по формуле

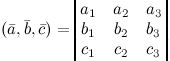
Билет 18

Пло́скость — это поверхность, образованная кинематическим движением образующей по направляющей, представляющей из себя прямую (начертательная геометрия).

• Общее уравнение (полное) плоскости

где  и  — постоянные, причём  и  одновременно не равны нулю; в векторной форме:

• Уравнение плоскости в отрезках:

• Уравнение плоскости, проходящей через точку 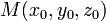 перпендикулярно вектору нормали :

• авнение плоскости, проходящей через три заданные точки 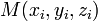, не лежащие на одной прямой:

(смешанное произведение векторов), иначе

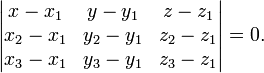
_{Билет 20}

Матрицей размера  называется прямоугольная таблица специального вида, состоящая из  строк и  столбцов, заполненная некоторыми элементами.

Количество строк и столбцов матрицы задают ее размеры.

Обозначение: 

Элементы матрицы  обозначаются , где  - номер строки, в которой находится элемент, а  - номер столбца.

Матрица размера  называется квадратной, число  называется порядком матрицы.

Матрица  называется нулевой, если все её элементы равны нулю, т.е. .

Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, - вектор-столбцом.

Квадратная матрица  называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.

Скалярной называется диагональная матрица , у которой все диагональные элементы равны между собой.

Единичной матрицей  называется скалярная матрица порядка ,диагональные элементы которой равны 1.

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Суммой матриц  и  одного размера называется матрица такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Произведением матрицы  на матрицу  называется матрица  такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы  на соответствующие элементы -ого столбца матрицы .

Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Билет 21

Квадратной матрице Квадратная матрица -го порядка ставиться в соответствие число Определитель матрицы, называемое определителем матрицы или детерминантом.

 При транспонировании квадратной матрицы её определитель не меняется:

Общий множитель в строке можно выносить за знак определителя.

 

То есть, если квадратная матрица  -го порядка умножается на некоторое ненулевое число , то определитель полученной матрицы равен произведению определителя исходной матрицы  на число  в степени, равной порядку матриц.

Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

Если две строки определителя поменять местами, то определитель поменяет знак.

 Определитель с двумя равными строками равен нулю.

Определитель с двумя пропорциональными строками равен нулю.

Определитель, содержащий нулевую строку, равен нулю.

Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

 Определитель произведения матриц равен произведению определителей:

Билет 23

Сиистемой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индексiобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например, 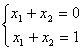, если бы решение существовало, то x₁ + x₂равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

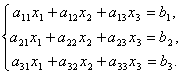
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

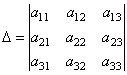
называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

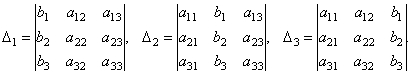
Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

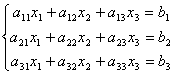Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим наа₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

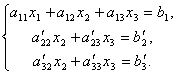
Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

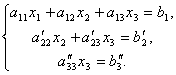
Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

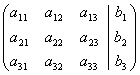
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

Рангом системы строк называется максимальное количество линейно независимых строк этой системы.

Рангом матрицы  называется ранг её системы строк или столбцов.

Обозначается 

На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.

Билет 24

Однородная система всегда совместна. Решение  () называется нулевым, или тривиальным.

Однородная система (6.1) имеет ненулевое решение тогда и только тогда, когда ее ранг () меньше числа неизвестных. В частности, однородная система, в которой число уравнений равно числу неизвестных, обладает ненулевым решением тогда и только тогда, когда ее определитель равен нулю.

Поскольку на этот раз все , вместо формул (6.6) получим следующие:

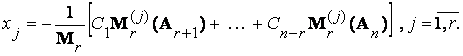(6.7)

          Формулы (6.7) содержат любое решение однородной системы (6.1).

         1. Совокупность всех решений однородной системы линейных уравнений (6.1) образует линейное пространство.

2. Линейное пространство R всех решений однородной системы линейных уравнений (6.1) с n неизвестными и рангом основной матрицы, равным r, имеет размерность n – r.

Любая совокупность из (n – r) линейно независимых решений однородной системы (6.1) образует базис в пространствеR всех решений. Она называется фундаментальной совокупностью решений однородной системы уравнений (6.1). Особо выделяют «нормальную» фундаментальную совокупность решений однородной системы (6.1):

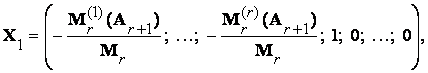
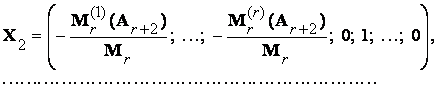
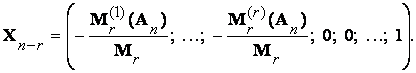(6.8)

         По определению базиса, любое решение Х однородной системы (6.1) представимо в виде

                                                         (6.9)

где  – произвольные постоянные.

Поскольку в формуле (6.9) содержится любое решение однородной системы (6.1), то она дает общее решение этой системы.

Пример. 

      

В качестве базисного минора  возьмем

.

Из формул (6.8) получим

Общее решение исходной системы имеет вид

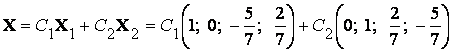
Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Билет 25

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Билет 31

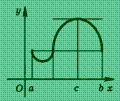
Теорема Ролля. Если функция у = f (х),  непрерывная на отрезке [а ; b] и  дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.  Геометрически эта теорема означает  следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).    Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и  дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что  

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х)  между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ.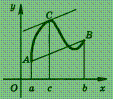  

Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.  

Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];  

2)  дифференцируемы в интервале (а ; b);  

3) g'(x) ≠ 0 в этом  интервале,  

то в интервале (а ; b) существует  такая точка с, что имеет место равенство 

 

Билет 30

Для любой алгебраической поверхности второго порядка существует прямоугольная система координат Oxyz, в которой уравнение этой поверхности принимает один из следующих семнадцати канонических видов: