
- •Функция называется бесконечно малой функцией (б.М.Ф.) при (или в точке ), если Основные свойства бесконечно малых функций
- •Функция определена в точке и ее окрестности;
- •Существует конечный предел функции в точке ;
- •Это предел равен значению функции в точке , т.Е.
- •Свойства скалярного произведения:
- •Свойства векторного произведения:
- •Свойства смешанного произведения:
Билет №1
Число ![]() называется пределом
функции
называется пределом
функции ![]() на
бесконечности или
при
на
бесконечности или
при ![]() ,
если для любого
,
если для любого ![]() существует
число
существует
число![]() такое,
что для всех
такое,
что для всех ![]() из
того, что
из
того, что ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
.
Число ![]() называется пределом
функции
называется пределом
функции ![]() в
точке
в
точке ![]() ,
если для
,
если для![]()
![]() такое,
что для
такое,
что для ![]() из
того, что
из
того, что![]() следует,
что
следует,
что ![]() :
: ![]() или
или![]() при
при ![]() .
.
Число ![]() называется пределом
функции
называется пределом
функции ![]() в
точке
в
точке ![]() ,
если для любой последовательности
,
если для любой последовательности ![]() ,
которая сходится к
,
которая сходится к ![]() ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции ![]() сходится
к
сходится
к ![]() .
.
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Число ![]() называется правым
пределом функции
называется правым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для ![]()
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается ![]()
Число ![]() называется левым
пределом функции
называется левым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для ![]()
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
2). Левый предел обозначается
(рис.
2). Левый предел обозначается ![]()
Билет №2
Функция называется бесконечно малой функцией (б.М.Ф.) при (или в точке ), если Основные свойства бесконечно малых функций
1° Сумма конечного числа б.м функций является функцией б.м.
2° Произведение б.м функции на ограниченную есть функция б.м.
3° Произведение двух б.м функций есть функция б.м.
4° Произведение б.м функции на константу является б.м функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6°
Функция ![]() ,
обратная к б.м функции
,
обратная к б.м функции ![]() ,
есть функция бесконечно большая. Верно
и обратное.
,
есть функция бесконечно большая. Верно
и обратное.
(Правило Лопиталя).
Пусть
функции ![]() и
и ![]() удовлетворяют
следующим условиям:
удовлетворяют
следующим условиям:
1)
эти функции дифференцируемы в окрестности
точки ![]() ,
кроме, может быть, самой точки
,
кроме, может быть, самой точки ![]() ;2)
;2) ![]() и
и ![]() в
этой окрестности;
в
этой окрестности;
3) ![]() ;
;
4) ![]() существует
конечный или бесконечный.
существует
конечный или бесконечный.
Тогда
существует и ![]() ,
причем
,
причем ![]()
Билет №3
Функция ![]() называется непрерывной
в точке
называется непрерывной
в точке ![]() ,
если:
,
если:
-
функция
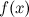 определена
в точке
определена
в точке  и
ее окрестности;
и
ее окрестности; -
существует конечный предел функции
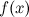 в
точке
в
точке  ;
; -
это предел равен значению функции в точке
 ,
т.е.
,
т.е. 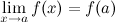
-
Функция, непрерывная во всех точках некоторой области, называетсянепрерывной в этой области.
-
Функция
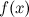 называется непрерывной
справа в точке
называется непрерывной
справа в точке  ,
если
,
если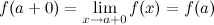 .
. -
Функция
 называется непрерывной
слева в точке
называется непрерывной
слева в точке  ,
если
,
если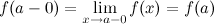 .
. -
Функция
 называется непрерывной
в интервале
называется непрерывной
в интервале  ,
если она непрерывна в каждой точке
этого интервала.
,
если она непрерывна в каждой точке
этого интервала. -
Функция
 называется непрерывной
на отрезке
называется непрерывной
на отрезке  ,
если она является непрерывной в
интервале
,
если она является непрерывной в
интервале  ,
непрерывной справа в точке
,
непрерывной справа в точке  ,
то есть
,
то есть 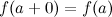 и
непрерывной слева в точке
и
непрерывной слева в точке  ,
то есть
,
то есть 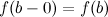 .
.
Точка ![]() ,
в которой нарушено хотя бы одно из трех
условийнепрерывности
функции,
а именно:
,
в которой нарушено хотя бы одно из трех
условийнепрерывности
функции,
а именно:
-
Функция определена в точке и ее окрестности;
-
Существует конечный предел функции в точке ;
-
Это предел равен значению функции в точке , т.Е.
называется точкой разрыва функции.
Если
в точке ![]() существуют
конечные пределы
существуют
конечные пределы ![]() и
и ![]() ,
такие, что
,
такие, что ![]() ,
то точка
,
то точка ![]() называется точкой
разрыва первого рода.
называется точкой
разрыва первого рода.
Если
хотя б один из пределов ![]() или
или ![]() не
существует или равен бесконечности, то
точка
не
существует или равен бесконечности, то
точка ![]() называется точкой
разрыва второго рода.
называется точкой
разрыва второго рода.
Если
существуют левый
и правый пределы функции в
точке и они равны друг другу, но не
совпадают со значением функции ![]() в
точке
в
точке ![]() :
: ![]() или
функция
или
функция ![]() не
определена в точке
не
определена в точке ![]() ,
то точка
,
то точка ![]() называется точкой
устранимого разрыва.
называется точкой
устранимого разрыва.
Билет 4
Производная функции:
Производной от функции f в точке х наз. предел отношения её приращения y в этой точке к соответствующему приращению аргумента x, когда последнее стремится к нулю. Производную принято обозначать так:
f'(x)=lim(x0)y/x=lim(x0)f(x+x)–f(x)/x (1)
Геометрический смысл производной:
П усть
на интервале (а,b)
задана непрерывная функция у=f(x).
Её график наз. непрерывной кривой.
Обозначим его через Г. Зададим на Г
точку А=(х,f(х)) (рис)
и поставим целью определить касательную
к Г в этой точке.
усть
на интервале (а,b)
задана непрерывная функция у=f(x).
Её график наз. непрерывной кривой.
Обозначим его через Г. Зададим на Г
точку А=(х,f(х)) (рис)
и поставим целью определить касательную
к Г в этой точке. ![]() Для
этого введем на Г другую точку
B=(x+x,f(x+x)),
где x0
(рис. 1 изображён случай x>0,
а на рис. 2 – случай x<0).
Прямую, проходящую через точки А и
В, направленную в сторону возрастания
х (отмеченную стрелкой), наз. секущей
и обозначим через S. Угол,
который S образует с
положительным направлением оси х,
обозначим через .
Мы считаем, что –/2<<
/2. При >0
угол отсчитывается от оси x против
часовой стрелки, а при <0
по часовой стрелке. На данных рисунках
>0. На рис. 1 x=AC,
y=СВ,
а на рис. 2 x=–AC,
y=–СВ,
В обоих случаях y/x=tg.
Для
этого введем на Г другую точку
B=(x+x,f(x+x)),
где x0
(рис. 1 изображён случай x>0,
а на рис. 2 – случай x<0).
Прямую, проходящую через точки А и
В, направленную в сторону возрастания
х (отмеченную стрелкой), наз. секущей
и обозначим через S. Угол,
который S образует с
положительным направлением оси х,
обозначим через .
Мы считаем, что –/2<<
/2. При >0
угол отсчитывается от оси x против
часовой стрелки, а при <0
по часовой стрелке. На данных рисунках
>0. На рис. 1 x=AC,
y=СВ,
а на рис. 2 x=–AC,
y=–СВ,
В обоих случаях y/x=tg.
Определение: Касательной к кривой Г (y=f(x)) в её точке А=(х,f(х)) наз. направленная прямая Т, к которой стремится секущая S (направленная в сторону возрастания х прямая), проходящая через А и точку В=(x+x,f(x+x))Г, когда x>0. Мы доказали, что если непрерывная, функция у=f(х) имеет конечную производную f'(х) в точке х, то её график Г в соответствующей точке имеет касательную с угловым коэффициентом tg=f'(х) (–/2<</2). Обратно, существование предела lim=(–/2<</2)
влечет за собой существование конечной производной f'(х) и справедливость равенств (1), (2). Может случиться, что f имеет в точке х правую и левую производные, отличные между собой: f'(x)f'пр(x).
Билет №5
Производная сложной функции:
Теорема №1: Если функция x=(t) имеет производную в точке t, а функция y=f(x) имеет производную в точке х, то сложная функция у=F(t)=f[(t)] (1) имеет производную (по t) в точке t и справедлива равенство F'(t)=f'(x)'(t) (2) или y't=y'xx't (3) Доказательство: Зададим t, ему соответствует значение х=(t). Придадим t приращение t0. это вызовет приращение x=(t+t)– (t). Так как функция y=f(x) имеет производную в точке х, то на основании равенства f'(x)=lim(x0)y/x=lim(x0)f(x+x)–f(x)/x, имеем
y=f'(x)x+(x)x (4), где (x)0 при х0. Будем считать, что (0)=0. Равенство (4) при этом соглашении выполняется, т.к. если подставить в него x=0, то получится 0=0. Разделим теперь равенство (4) на t0: y/t=f'(x)(x/t)+ (x)(x/t) (5). Пусть t0. Тогда, потому что функция x(t)(t) имеет производную в точке t и, =>, непрерывна. Переходим в равенстве (5) к пределу при t0. Тогда x0 и (x)0, поэтому получим y't=f'(x)x'(t)+0x'(t)=f'(x)x'(t)=y'xx't. Теорема доказана.
Формула (1) может быть усложнена. Например, если – z=f(y), y=(x), x=() и все три функции имеют производные в соответствующих точках, то z'=z'yy'xx'
Суть
такого дифференцирования заключается
в следующем: вначале находитсялогарифм заданной
функции, а уже затем вычисляется от него
производная. Пусть задана некоторая
функция ![]() .
Прологарифмируем левую и правую части
данного выражения:
.
Прологарифмируем левую и правую части
данного выражения:
![]()
Далее
продифференцируем полученное равенство
при условии, что ![]() является
функцией от
является
функцией от ![]() ,
то есть найдем производную
сложной функции:
,
то есть найдем производную
сложной функции:
![]()
А
тогда, выражая искомую производную ![]() ,
в результате имеем:
,
в результате имеем:
![]()
Билет 6
Пусть
функция ![]() дифференцируема
в точке
дифференцируема
в точке ![]() ,
то есть приращение этой функции можно
представить в виде суммы двух слагаемых:
линейного относительно
,
то есть приращение этой функции можно
представить в виде суммы двух слагаемых:
линейного относительно ![]() и
нелинейного членов:
и
нелинейного членов:
![]()
где ![]() при
при ![]() .
.
Определение
Дифференциалом
функции называется
линейная относительно ![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как ![]() или
или ![]() .
Таким образом:
.
Таким образом:
![]()
Константу можно выносить за знак дифференциала.
![]()
2. Дифференциал суммы/разности.
Дифференциал суммы/разности функций равен суме/разности дифференциалов от каждого из слагаемых.
![]()
3. Дифференциал произведения.
![]()
4. Дифференциал частного.
![]()
Билет 7
Если
функция ![]() имеет
производную в каждой точке
имеет
производную в каждой точке ![]() своей
области определения, то ее производная
своей
области определения, то ее производная ![]() есть
функция от
есть
функция от ![]() .
Функция
.
Функция ![]() ,
в свою очередь, может иметь производную,
которую называют производной
второго порядка функции
,
в свою очередь, может иметь производную,
которую называют производной
второго порядка функции ![]() (или второй
производной)
и обозначают символом
(или второй
производной)
и обозначают символом ![]() .
Таким образом
.
Таким образом
![]()
Дифференциалом ![]() -го
порядка
-го
порядка ![]() функции
функции ![]() называется
дифференциал от дифференциала
называется
дифференциал от дифференциала ![]() -го
порядка этой функции, то есть
-го
порядка этой функции, то есть
![]()
ейбница формула
формула, выражающая производную n-го порядка (см. Дифференциальное исчисление) от произведения двух функций через производные сомножителей:
![]()
.
Эта формула была сообщена Г. Лейбницем в письме к И. Бернулли в 1695. Л. ф. облегчает вычисление производных высших порядков.
Билет 8
Для
произвольной функции ![]() ,
не являющейся многочленом, формула
Тейлора в окрестности некоторой
точки
,
не являющейся многочленом, формула
Тейлора в окрестности некоторой
точки ![]() принимает
вид:
принимает
вид:
![]()
Последнее
слагаемое ![]() называется остаточным
членом в форме Пеано.
называется остаточным
членом в форме Пеано.
Ф ормула
(3') наз. формулой
Тейлора с остаточным членом в форме
Лагранжа.
ормула
(3') наз. формулой
Тейлора с остаточным членом в форме
Лагранжа.
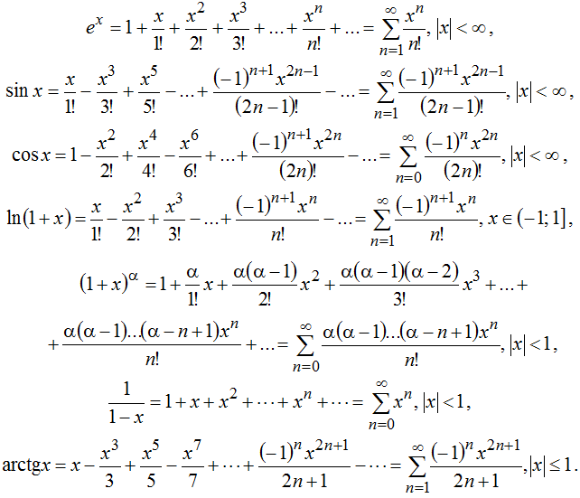
Билет 9
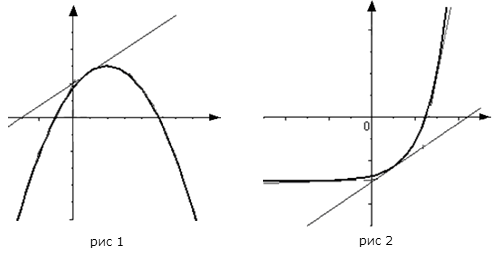
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале ![]() ,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала
,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала ![]() лежит
не выше любой своей касательной (рис.
1).
лежит
не выше любой своей касательной (рис.
1).
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале ![]() ,
является на этом интервале вогнутым,
если график этой функции в пределах
интервала
,
является на этом интервале вогнутым,
если график этой функции в пределах
интервала ![]() лежит
не ниже любой своей касательной (рис.
2).
лежит
не ниже любой своей касательной (рис.
2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть
функция ![]() определена
на интервале
определена
на интервале ![]() и
имеет непрерывную, не равную нулю в
точке
и
имеет непрерывную, не равную нулю в
точке ![]() вторую
производную. Тогда, если
вторую
производную. Тогда, если ![]() всюду
на интервале
всюду
на интервале ![]() ,
то функция имеет вогнутость
на этом интервале,
если
,
то функция имеет вогнутость
на этом интервале,
если ![]() ,
то функция имеет выпуклость.
,
то функция имеет выпуклость.
Определение
Точкой
перегиба графика
функции ![]() называется
точка
называется
точка ![]() ,
разделяющая промежутки выпуклости и
вогнутости.
,
разделяющая промежутки выпуклости и
вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если
функция ![]() имеет
перегиб в точке
имеет
перегиб в точке ![]() ,
то
,
то![]() или
не существует.
или
не существует.
Функция ![]() называется строго
возрастающей на промежутке,
если большему значению аргумента из
этого промежутка соответствует большее
значение функции, т.е.
называется строго
возрастающей на промежутке,
если большему значению аргумента из
этого промежутка соответствует большее
значение функции, т.е.
![]()
Функция ![]() называется строго
убывающей на промежутке,
если большему значению аргумента из
этого промежутка соответствует меньшее
значение функции, т.е.
называется строго
убывающей на промежутке,
если большему значению аргумента из
этого промежутка соответствует меньшее
значение функции, т.е.
![]()
Если
производная функции ![]() на
некотором промежутке
на
некотором промежутке ![]() ,
то функция
,
то функция ![]() возрастает
на этом промежутке; если же
возрастает
на этом промежутке; если же![]() на
промежутке
на
промежутке ![]() ,
то функция
,
то функция ![]() убывает
на этом промежутке.
убывает
на этом промежутке.
Точка ![]() называется точкой
локального максимума функции
называется точкой
локального максимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности выполняется
неравенство:
из
этой окрестности выполняется
неравенство: ![]() .
.
Точка ![]() называется точкой
локального минимума функции
называется точкой
локального минимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности
из
этой окрестности ![]() .
.
Если
функция ![]() имеет
экстремум в точке
имеет
экстремум в точке ![]() ,
то ее производная
,
то ее производная ![]() либо
равна нулю, либо не существует.
либо
равна нулю, либо не существует.
Билет 10
Теорема Лагранжа:
Пусть функция f(x) непрерывна на отрезке [а,b] и имеет производную на интервале (а,b). Тогда существует на интервале (а,b) точка с, для которой выполняется равенство f(b)–f(a)=(b-a)f'(c) при (а<с<b){1}. Теорема Лагранжа имеет простой геометрический .смысл, если записать её в виде (f(b)–f(a))/(b–a)=f'(c) при (а<с<b).

Билет 11
Функция ![]() называется первообразной для
функции
называется первообразной для
функции ![]() на
промежутке
на
промежутке ![]() ,
конечном или бесконечном, если
функция
,
конечном или бесконечном, если
функция ![]() дифференцируема в
каждой точке этого промежутка и ее
производная удовлетворяет следующему
равенству:
дифференцируема в
каждой точке этого промежутка и ее
производная удовлетворяет следующему
равенству:
![]()
Совокупность
всех первообразных функции ![]() ,
определенных на заданном промежутке,
называется неопределенным
интегралом от функции
,
определенных на заданном промежутке,
называется неопределенным
интегралом от функции ![]() и
обозначается символом
и
обозначается символом ![]() .
То есть
.
То есть
![]()
Знак ![]() называется интегралом,
называется интегралом, ![]() - подынтегральным
выражением,
- подынтегральным
выражением, ![]() - подынтегральной
функцией,
а
- подынтегральной
функцией,
а ![]() - переменной
интегрирования.
- переменной
интегрирования.
Операция
нахождения первообразной или
неопределенного интеграла от
функции ![]() называется интегрированием
функции
называется интегрированием
функции![]() .
Интегрирование представляет собой
операцию, обратную дифференцированию.
.
Интегрирование представляет собой
операцию, обратную дифференцированию.

Если
в неопределенном
интеграле ![]() сделать
подстановку
сделать
подстановку ![]() ,
где функция
,
где функция ![]() -
функция с непрерывной первой производной,
то тогда
-
функция с непрерывной первой производной,
то тогда![]() и
согласно свойству
6 неопределенного интеграла имеем,
что:
и
согласно свойству
6 неопределенного интеграла имеем,
что:
![]()
Эта формула называется формулой замены переменной в неопределенном интеграле.
Проинтегрировав левую и правую части последнего равенства, получим:
![]()
Полученное равенство перепишем в виде:
![]()
Эта
формула называется формулой
интегрирования по частям.
С ее помощью интеграл ![]() можно
свести к нахождению интеграла
можно
свести к нахождению интеграла ![]() ,
который может быть более простым.
,
который может быть более простым.
Билет 12
Если
существует конечный предел интегральной
суммы (1) и он не зависит ни от способа
разбиения отрезка ![]() на
частичные отрезки, ни от выбора точек
на
частичные отрезки, ни от выбора точек ![]() в
них, то этот предел называется определенным
интегралом от функции
в
них, то этот предел называется определенным
интегралом от функции ![]() на
отрезке
на
отрезке ![]() и
обозначается
и
обозначается 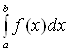 .
.
Таким
образом,  .
.
В
этом случае функция ![]() называется
интегрируемой на
называется
интегрируемой на ![]() .
Числа а и b называются соответственно
нижним и верхним пределами интегрирования,
.
Числа а и b называются соответственно
нижним и верхним пределами интегрирования, ![]() –
подынтегральной функцией,
–
подынтегральной функцией, ![]() –
подынтегральным выражением,
–
подынтегральным выражением, ![]() –
переменной интегрирования;
отрезок
–
переменной интегрирования;
отрезок ![]() называется
промежутком интегрирования.
называется
промежутком интегрирования.
Пусть
на отрезке ![]() задана
непрерывная неотрицательная
функция
задана
непрерывная неотрицательная
функция ![]() . Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y = f(x),
снизу – осью Ох, слева и справа –
прямыми x = a и x = b (рис. 2).
. Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y = f(x),
снизу – осью Ох, слева и справа –
прямыми x = a и x = b (рис. 2).

Рис. 2
Определенный
интеграл 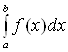 от
неотрицательной функции
от
неотрицательной функции ![]() с
геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
с
геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции ![]() ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых ![]() и
и ![]() ,
снизу – отрезком
,
снизу – отрезком ![]() оси
Ох.
оси
Ох.
Физический смысл определенного интеграла:
Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t1 до t2, вычисляется по формуле
S=![]() t2t1v(t)dt
t2t1v(t)dt
Билет 13
Рассмотрим
функцию ![]() ,
заданную на отрезке
,
заданную на отрезке ![]() ,
и предположим, что она интегрируема на
отрезке
,
и предположим, что она интегрируема на
отрезке ![]() .
Тогда при любом
.
Тогда при любом ![]() эта
функция будет интегрируема на отрезке
эта
функция будет интегрируема на отрезке ![]() и,
следовательно, функция
и,
следовательно, функция

определена
при всех ![]() .
При
.
При ![]() мы
по определению положим её равной 0, то
есть будем считать, что
мы
по определению положим её равной 0, то
есть будем считать, что ![]() для
любой функции
для
любой функции ![]() и
точки
и
точки ![]() из
её области определения. Итак,
функция
из
её области определения. Итак,
функция ![]() равняется
значению определённого интеграла с
переменным верхним пределом, вычисленного
от интегрируемой функции
равняется
значению определённого интеграла с
переменным верхним пределом, вычисленного
от интегрируемой функции ![]() ,
не обязательно непрерывной.
Формула Ньютона — Лейбница или основная
теорема анализа даёт
соотношение между двумя операциями:
взятиемопределённого
интеграла и
вычислением первообразной.
,
не обязательно непрерывной.
Формула Ньютона — Лейбница или основная
теорема анализа даёт
соотношение между двумя операциями:
взятиемопределённого
интеграла и
вычислением первообразной.
-
Если
 непрерывна
на отрезке
непрерывна
на отрезке  и
и  —
её любая первообразная на этом
отрезке, то имеет место равенство
—
её любая первообразная на этом
отрезке, то имеет место равенство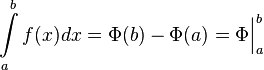
Теорема. Пусть
дан интеграл  ,
где
,
где ![]() непрерывна
на
непрерывна
на ![]() .
Введем новую переменную
.
Введем новую переменную ![]() ,
связанную с
,
связанную с ![]() равенством
равенством ![]() .
Если
.
Если
1) ![]()
2) ![]() и
и ![]() непрерывны
на
непрерывны
на ![]() ,
,
3) при
изменении z от α до β значения ![]() не
выходят за пределы отрезка
не
выходят за пределы отрезка ![]() то
то
|
|
(5)
|
Формула
интегрирования по частям в определенном
интеграле выводится так же, как и для
неопределенного интеграла, и имеет
вид ![]()
Билет 16
Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому.
Сложение
векторов ![]() и
и ![]() осуществляется
по правилу
треугольника.
осуществляется
по правилу
треугольника.
Суммой ![]() двух
векторов
двух
векторов ![]() и
и ![]() называют
такой третий вектор
называют
такой третий вектор ![]() ,
начало которого совпадает с началом
,
начало которого совпадает с началом ![]() ,
а конец - с концом
,
а конец - с концом ![]() при
условии, что конец вектора
при
условии, что конец вектора ![]() и
начало вектора
и
начало вектора ![]() совпадают
(рис. 1).
совпадают
(рис. 1).

Для сложения векторов применяется также правило параллелограмма.
Определение
Правило
параллелограмма -
если два неколлинеарных вектора ![]() и
и ![]() привести
к общему началу, то вектор
привести
к общему началу, то вектор ![]() совпадает
с диагональю параллелограмма, построенного
на векторах
совпадает
с диагональю параллелограмма, построенного
на векторах ![]() и
и ![]() (рис.
2). Причем начало вектора
(рис.
2). Причем начало вектора ![]() совпадает
с началом заданных векторов.
совпадает
с началом заданных векторов.
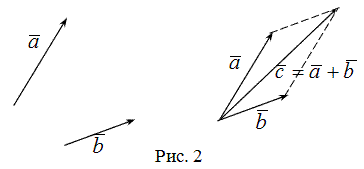
Разностью ![]() векторов
векторов ![]() и
и ![]() называется
вектор
называется
вектор ![]() такой,
что выполняется условие:
такой,
что выполняется условие: ![]() (рис.
3).
(рис.
3).
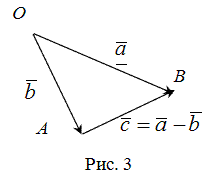
Скалярным
произведением двух
ненулевых векторов ![]() и
и ![]() называется
число, равное произведению длин этих
векторов на косинус угла между ними:
называется
число, равное произведению длин этих
векторов на косинус угла между ними:
![]()
Если
векторы ![]() и
и ![]() заданы
своими координатами:
заданы
своими координатами: ![]() ,
, ![]() ,
то их скалярное произведение вычисляется
по формуле:
,
то их скалярное произведение вычисляется
по формуле:
1
![]()

