Односторонние пределы

Пусть Х – область определения функции, которая, быть может, не содержит точку , но для любогоправая полуокрестность точки(интервал) содержит точки множества Х.

ОПРЕДЕЛЕНИЕ 7 (правый предел функции в точке по Гейне). Числоназывается правым пределом функциив точке, если для любой последовательности значений ее аргумента, сходящейся ки состоящей их чисел, большихсоответствующая последовательность значений функцийсходится к. Обозначение:

ОПРЕДЕЛЕНИЕ 8 (правый предел функции в точке по Коши). Числоназывается правым пределом функциив точке, если,

Для определения левого предела будем считать, что любая левая полуокрестность точки , интервал, содержит точки Х.

ОПРЕДЕЛЕНИЕ 9 (левый предел функции в точке по Гейне). Числоназывается левым пределом функциив точке, если для любой последовательности значений ее аргумента, сходящейся ки состоящей их чисел, меньшихсоответствующая последовательность значений функцийсходится к. Обозначение:

ОПРЕДЕЛЕНИЕ 10 (левый предел функции в точке по Коши). Числоназывается левым пределом функциив точке, если,

ПРИМЕР. Найти односторонние пределы (правый и левый) функции

в точках и.

Так как справа от 0 и близко к нему тоОчевидно,

что хорошо видно на графике функции (рис. 5):

y 1 -1 О 2 4 x Рис. 5

Существуют ли и? Не существуют, так как левый предел не равен правому пределу в этих точках. Имеет место утверждение:

для того, чтобы функция имела в точке предел , необходимо и достаточно, чтобы в этой точке существовали равные односторонние пределы.

ПРИМЕР. Найти односторонние пределы функции в точке

ПРИМЕР. Найти односторонние пределы функции в точке

y 1 О 1 2 x Рис. 6

Предел функции в этой точке существует, так как односторонние пределы равны (рис.6).

Сравнение бесконечно малых

ОПРЕДЕЛЕНИЕ. Функция называетсябесконечно малой (б.м.) в точке если

ПРИМЕРЫ. – б.м. в точках– б.м. в точках– б.м. в точке

Пусть и– б.м. в точкето естьПредел отношения б.м. функцийназываетсянеопределенностью вида

ПРИМЕР. – б.м. в точке

ОПРЕДЕЛЕНИЕ. 1) Б.м. в точке функцияимеетболее высокий порядок малости, чем , если

2) Б.м. в точке функциииодного порядка малости, если

3) Б.м. в точке функции эквивалентны, если

.

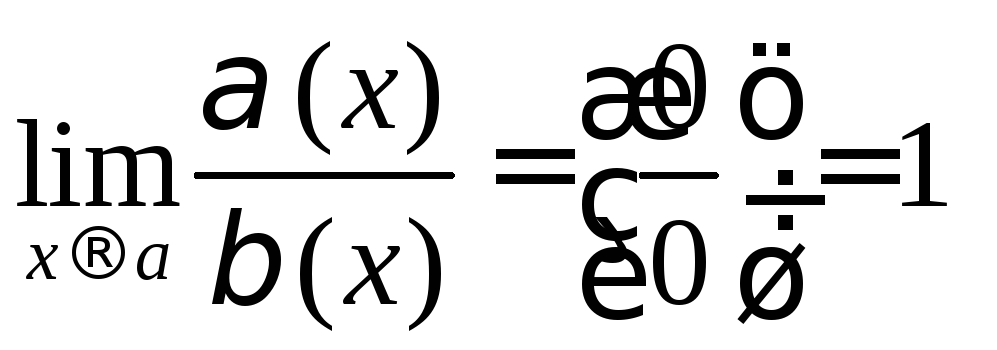Эквивалентные б.м. обозначаются так:

ПРИМЕР. имеет более высокий порядок малости в точке, чеми

и одного порядка малости.

ПРИМЕР. Сравнить функции и, б.м. в точке

Вычислим предел отношения:

в точке

ТЕОРЕМА (принцип замены эквивалентных бесконечно малых). Пусть б.м. функции в точкеиТогда

ДОКАЗАТЕЛЬСТВО. Так как то

Что и требовалось доказать.