Предельный переход в неравенствах

ТЕОРЕМА 10 (о предельном переходе в неравенстве). Пусть и, начиная с некоторого номера,Тогда

ДОКАЗАТЕЛЬСТВО. Пусть Докажем, что тогда. Предположим противное:Так каксходится, то по определению 2ПустьТогда– противоречие, так как по условию. Таким образом, сделанное предположение неверно и

Случай рассматривается аналогично.

ЗАМЕЧАНИЕ. Предельный переход не сохраняет строгое неравенство, то есть, если то

ПРИМЕР. но

ТЕОРЕМА 11. Пусть и, начиная с некоторого номера,Тогда

Доказать самостоятельно, используя теоремы 7,10 для .

ТЕОРЕМА 12 (принцип двустороннего ограничения). Пусть кроме того, начиная с некоторого номера,Тогдасходится и

ДОКАЗАТЕЛЬСТВО.

Пусть (1)

По определению 2 (2)

и (3)

Зададим произвольное ПустьТогда неравенства (1),(2),(3) верныЭто означает по определению 2, чтосходится и, что и требовалось доказать.

Монотонные последовательности

ОПРЕДЕЛЕНИЕ. называется неубывающей (невозрастающей), еслиНеубывающая или невозрастающая последовательность называетсямонотонной.

ОПРЕДЕЛЕНИЕ. называется возрастающей (убывающей), еслиВозрастающая или убывающая последовательность называетсястрого монотонной.

ПРИМЕРЫ. а) – убывающая.

б) монотонной не является.

в) – возрастающая.

Заметим, что Таким образом, всякая монотонная последовательность ограничена с одной стороны, именно: неубывающая – снизу, невозрастающая – сверху. Значит, для ограниченности неубывающей последовательности необходимо, чтобы она была ограничена сверху, для невозрастающей – снизу.

ТЕОРЕМА 13. Если неубывающая последовательность ограничена сверху, то она сходится. Если невозрастающая последовательность ограничена снизу, то она также сходится.

Без доказательства.

Из теорем 5,13 следует теорема 14.

ТЕОРЕМА 14. Для того, чтобы монотонная последовательность сходилась, необходимо и достаточно, чтобы она была ограничена.

Рассмотрим последовательность

Можно показать, что возрастает, кроме того,, то естьмонотонна и ограничена. Следовательно, по теореме 14 она сходится, то естьпри этом по теореме 10Это число обозначают: оно иррационально, то есть представимо в виде бесконечной десятичной непериодической дроби, и

Таким образом, Это равенство называютвторым замечательным пределом.

Логарифм по основанию называютнатуральным:

Предел функции

Пусть функция определена на некотором множестве Х действительной оси, которое, быть может, не содержит точку, но содержит точки, бесконечно близкие кто естьокрестность этой точкисодержит точки множества Х.

ОПРЕДЕЛЕНИЕ 1 (предел функции в точке по Гейне). Числоназывается пределом функциив точке, если для любой

у b О a x Рис. 1

последовательности значений ее аргумента , сходящейся ки состоящей их чисел, отличных отсоответствующая последовательность значений функцийсходится к(рис.1). Этот факт обозначается так: .

ОПРЕДЕЛЕНИЕ 2 (предел функции в точке по Коши). Числоназывается пределом функциив точке, если

,

Это означает, что всегда найдется такой интервал, содержащий точку

y b b b О a a ax Рис. 2

, всюду внутри которого отличается оттак мало, как нам захочется. Так как по определению, тоЕсли, то, очевидно,верно неравенство(рис. 2).

ОПРЕДЕЛЕНИЕ 3 (предел функции на по Гейне) Числоназывается пределом функциипри, если для любой бесконечно большой последовательности значений ее аргумента, все члены которой положительны, соответствующая последовательность значений функциисходится к(рис. 3). Обозначение:

y b О x Рис. 3

ОПРЕДЕЛЕНИЕ 4 (предел функции на по Коши).

Число называется пределом функциипри, если(рис. 4).

y b b b 0 x Рис. 4

ОПРЕДЕЛЕНИЕ 5 (предел функции на по Гейне) Числоназывается пределом функциипри, если для любой бесконечно большой последовательности значений ее аргумента, все члены которой отрицательны, соответствующая последовательность значений функциисходится к. Обозначение:

ОПРЕДЕЛЕНИЕ 6 (предел функции на по Коши). Числоназывается пределом функциипри, если

Можно доказать, что определения предела по Коши и Гейне эквивалентны.

ПРИМЕР. Вычислить .

Рассмотрим функцию При всехВыберем произвольную последовательностьТогданезависимо от вида. По определению 1 это означает, что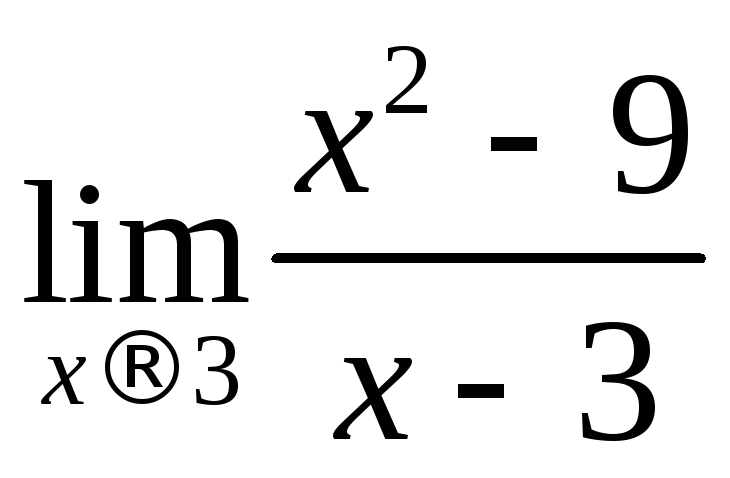=6.

ТЕОРЕМА (об арифметических операциях над функциями, имеющими предел). Пусть Тогда существуют пределы в точкефункций

и

ДОКАЗАТЕЛЬСТВО. По условию По определению 1 выберем произвольную,иТогда соответствующие последовательностиисходятся кисоответственно, то естьПо теоремам 6,7,8,9что и требовалось доказать.