Инвариантность формы первого дифференциала

По определению дифференциал (первый дифференциал) функции вычисляется по формулеесли– независимая переменная.

ПРИМЕР.

Покажем, что форма первого дифференциала остается неизменной (является инвариантной) и в том случае, когда аргумент функции сам является функцией, то есть для сложной функции.

Пусть дифференцируемы, тогда по определению

Кроме того, что и требовалось доказать.

ПРИМЕРЫ.

Доказанная инвариантность формы первого дифференциала позволяет считать, что то естьпроизводная равна отношению дифференциала функции к дифференциалу ее аргумента, независимо от того, является ли аргумент независимой переменной или функцией.

Дифференцирование функции, заданной параметрически

Пусть Если функцияимеет на множествеобратную, тоТогда равенстваопределяют на множествефункцию, заданную параметрически, – параметр (промежуточная переменная).

ПРИМЕР. Построить график функции .

y 1 О 1 x Рис. 25

Построенная кривая называется циклоидой (рис. 25) и является траекторией точки на окружности радиуса 1, которая катится без скольжения вдоль оси ОХ.

ЗАМЕЧАНИЕ. Иногда, но не всегда, из параметрических уравнений кривой можно исключить параметр.

ПРИМЕРЫ. 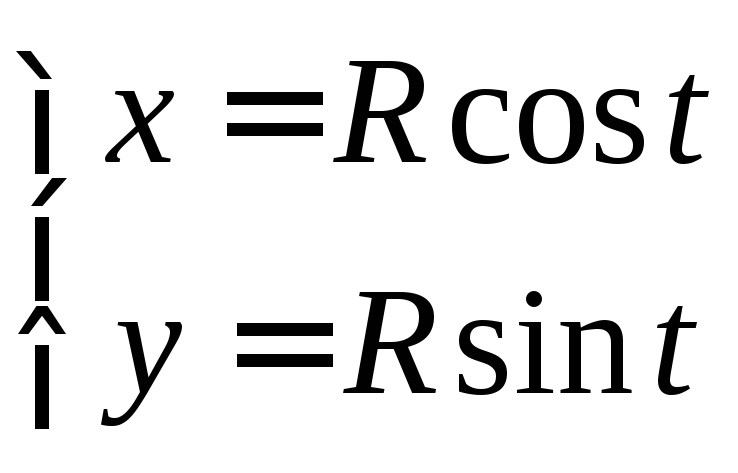– параметрические уравнения окружности, так как, очевидно,

–параметрические уравнения эллипса, так как

–параметрические уравнения параболы

Найдем производную функции, заданной параметрически:

Производная функции, заданной параметрически, – также функция, заданная параметрически: .

ОПРЕДЕЛЕНИЕ. Второй производной функции называется производная от ее первой производной.

Производной -го порядка называется производная от ее производной порядка.

Обозначают производные второго и -го порядка так:

Из определения второй производной и правила дифференцирования параметрически заданной функции следует, что Для вычисления третьей производной надо представить вторую производную в видеи воспользоваться еще раз полученным правилом. Производные старших порядков вычисляются аналогично.

ПРИМЕР. Найти производные первого и второго порядков функции

.

Основные теоремы дифференциального исчисления

ТЕОРЕМА (Ферма). Пусть функция имеет в точкеэкстремум. Если существует, то

ДОКАЗАТЕЛЬСТВО. Пусть , например, – точка минимума. По определению точки минимума существует окрестность этой точки, в пределах которой, то есть– приращениев точке. По определениюВычислим односторонние производные в точке:

по теореме о предельном переходе в неравенстве,

так как

, так как Но по условиюсуществует, поэтому левая производная равна правой, а это возможно лишь если

Предположение о том, что – точка максимума, приводит к тому же.

Геометрический смысл теоремы:

y О x Рис. 26

Если график функции имеет в точке экстремума касательную, то она параллельна оси ОХ (рис. 26).

ТЕОРЕМА (Ролля). Пусть функция непрерывна, дифференцируемаитогда существуеттакая, что

y a О b х Рис. 27

Геометрический смысл теоремы: если , то на графике дифференцируемой функции есть точки, в которых касательная параллельна оси ОХ (рис. 27).

ДОКАЗАТЕЛЬСТВО. Так как непрерывна, то по второй теореме Вейерштрасса она достигает насвоих наибольшегои наименьшегозначений либо в точках экстремума, либо на концах отрезка.

1. Пусть , тогда

2. Пусть Так както либо, либодостигается в точке экстремума, но по теореме ФермаЧто и требовалось доказать.

ТЕОРЕМА (Лагранжа). Пусть функция непрерывнаи дифференцируема, тогда существуеттакая, что.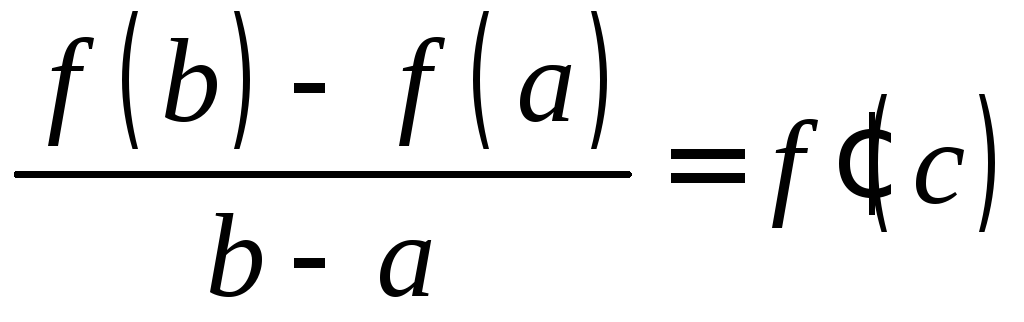

Геометрический смысл теоремы:

y B A a c О b х Рис. 28

АВ – секущая (рис. 28) и –угловой ее коэффициент. –угловой коэффициент касательной.

Так как , то секущая параллельна касательной. Таким образом, теорема утверждает, что существует касательная, параллельная секущей, проходящей через точки А и В.

ДОКАЗАТЕЛЬСТВО. Через точки Аи Впроведем секущую АВ. Ее уравнениеРассмотрим функцию

,

–расстояние между соответствующими точками на графике и на секущей АВ.

1. непрерывнакак разность непрерывных функций.

2. дифференцируемакак разность дифференцируемых функций.

3.

Значит, удовлетворяет условиям теоремы Ролля, поэтому существуеттакая, что

Теорема доказана.

ЗАМЕЧАНИЕ. Формула называетсяформулой Лагранжа.

ТЕОРЕМА (Коши). Пусть функции непрерывны, дифференцируемыи, тогда существует точкатакая, что.

ДОКАЗАТЕЛЬСТВО. Покажем, что . Если бы, то функцияудовлетворяла бы условию теоремы Ролля, поэтому существовала бы точкатакая, что– противоречие условию. Значит,, и обе части формулы определены. Рассмотрим вспомогательную функцию.

непрерывна , дифференцируемаи, то естьудовлетворяет условиям теоремы Ролля. Тогда существует точка, в которой, но

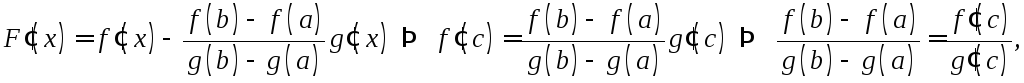
что и требовалось доказать.

Доказанная формула называется формулой Коши.

ПРАВИЛО Лопиталя (теорема Лопиталя-Бернулли). Пусть функции непрерывны, дифференцируемы,и. Кроме того, существует конечный или бесконечный.

Тогда существует

ДОКАЗАТЕЛЬСТВО. Так как по условию , то доопределимв точке, полагаяТогдастанут непрерывными. Покажем, чтоПредположим, чтотогда существуеттакая, что, так как функциянаудовлетворяет условиям теоремы Ролля. Но по условию– противоречие. Поэтому. Функцииудовлетворяют условиям теоремы Коши на любом отрезке, который содержится в. Напишем формулу Коши:

, .

Отсюда имеем: , так как если, то.

Переобозначая переменную в последнем пределе, получим требуемое:

ЗАМЕЧАНИЕ 1. Правило Лопиталя остается справедливым и в том случае, когда и. Оно позволяет раскрывать не только неопределенность вида, но и вида:

.

ЗАМЕЧАНИЕ 2. Если после применения правила Лопиталя неопределенность не раскрылась, то его следует применить еще раз.

ПРИМЕР.

ЗАМЕЧАНИЕ 3. Правило Лопиталя – универсальный способ раскрытия неопределенностей, но существуют пределы, раскрыть которые можно, применив лишь один из изученных ранее частных приемов.

ПРИМЕР. и так далее.

Но, очевидно, , так как степень числителя равна степени знаменателя, и предел равен отношению коэффициентов при старших степенях