8.4. Интегрирование по частям в определенном интеграле

Формула интегрирования по частям в определенном интеграле имеет вид: 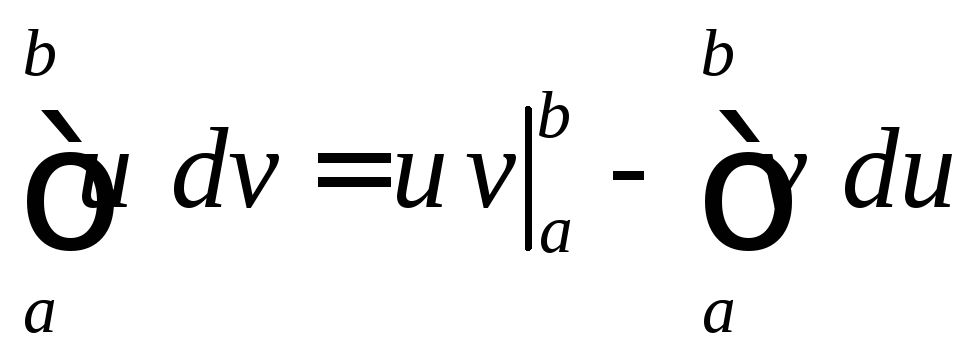(8.4)

ПРИМЕР. Вычислить .

.

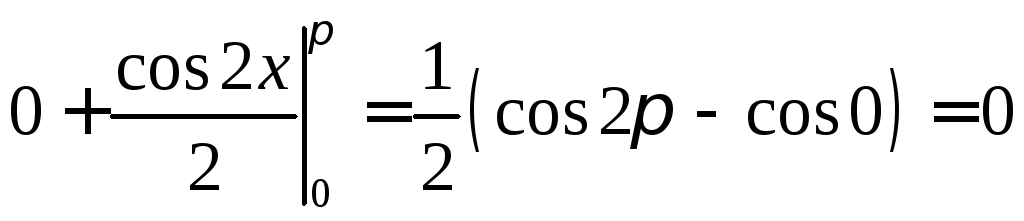8.5. Замена переменной в определенном интеграле

ТЕОРЕМА (о замене переменной в определенном интеграле). Пусть функция непрерывнаи. При этом

1)

2) непрерывны.

Тогда (8.5)

(8.5) – формула замены переменной в определенном интеграле.

ДОКАЗАТЕЛЬСТВО. Если – первообразная для функции, то по формуле Ньютона-Лейбница.

Функция , очевидно,– первообразная для функции, поэтому

.

Таким образом, левая и правая части формулы (8.5) равны, что и требовалось доказать.

ПРИМЕР. Вычислить .

Сделаем замену переменной по формуле . Тогда

.

Кроме того, если , то; если, то. Следовательно,

ЗАМЕЧАНИЕ. Следует обратить внимание на то, что при выполнении замены переменной в определенном интеграле, надо пересчитать пределы интегрирования, то есть найти отрезок, на котором изменяется новая переменная, но при этом к старой переменной возвращаться не надо.

СЛЕДСТВИЕ 1. Если – нечетная функция, непрерывная, то(рис. 16).

ДОКАЗАТЕЛЬСТВО. По определению нечетной функции .

Для вычисления воспользуемся свойством 3 аддитивности определённого интеграла:

.

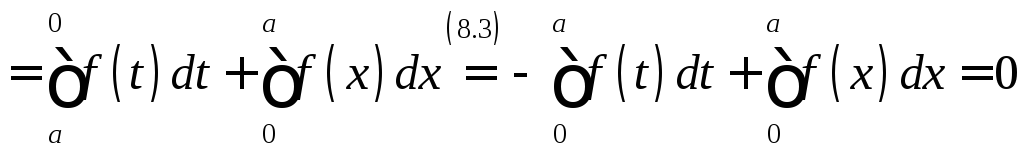ПРИМЕРЫ. Вычислить

а) ; б); в).

а) , так как произведение четной функциии нечетнойнечетно. Если не обратить внимание на нечётность подынтегральной функции, то для нахождения ее первообразной надо было бы дважды применить формулу интегрирования по частям (8.4).

б) .

При решении этой задачи мы воспользовались свойством 2 линейности определенного интеграла и тем, что функция – нечетная.

в)

.

СЛЕДСТВИЕ 2. Если – четная функция, непрерывная

, то (рис. 17). Доказать следствие 2 самостоятельно.

ПРИМЕР. В предыдущем примере

.

ЗАМЕЧАНИЕ. Исходя из геометрического смысла и свойств определенного интеграла можно, очевидно, утверждать, что и(рис 18).

–наименьший период функций . Для функций,наименьший период, поэтому, не находя первообразной и не пользуясь формулой Ньютона-Лейбница, можно сделать более общее утверждение (рис. 18):

, (8.6)

Более того (рис.19),

(8.7)

То есть определенный интеграл от нечетной степени синуса или косинуса по отрезку длиною в период равен нулю.

Кроме того, можно заметить, что величина определенного интеграла от периодической функции по отрезку, длина которого равна ее периоду, не зависит от положения отрезка интегрирования (рис. 20) на оси ОХ:

, Т – период функции .

Поэтому формулы (8.6), (8.7) справедливы и если , где– произвольное число.

ПРИМЕР. Вычислить: а) , б), в).

а) , так как длина отрезка интегрированияи наименьший период функции.

б) , так как,и на отрезке интегрирования помещается четыре полных периода, на каждом из которых этот интеграл равен нулю.

в)

.

Вычисляя этот интеграл, мы дважды воспользовались тригонометрическими формулами понижения степени, одной из формул (8.6) и свойством 1 определенного интеграла, при этом, заметим, не нашли ни одной первообразной.