
- •Н.И. Николаева интегральное исчисление
- •Часть 4
- •Оглавление
- •Глава 7. Неопределенный интеграл
- •7.1. Определение и свойства неопределенного интеграла
- •7.2. Основные формулы и методы интегрирования.
- •7.3. Замена переменной в неопределенном интеграле
- •7.4. Интегрирование по частям
- •7.5. Интегрирование рациональных дробей
- •7.6. Интегрирование некоторых тригонометрических функций
- •7.7. Интегрирование некоторых иррациональных выражений
- •Глава 8. Определенный интеграл
- •8.1. Определенный интеграл по фигуре
- •8.2. Определенный интеграл на отрезке
- •8.3. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница
- •8.4. Интегрирование по частям в определенном интеграле
- •8.5. Замена переменной в определенном интеграле
- •8.6. Геометрические приложения определенного интеграла на отрезке
- •8.7. Несобственные интегралы. Интегралы с бесконечными пределами интегрирования
- •8.8. Исследование сходимости несобственных интегралов с помощью признаков сравнения
- •8.9. Интегралы от неограниченных функций
8.2. Определенный интеграл на отрезке
Сформулированное выше определение определенного интеграла является неконструктивным: его очень непросто применить на практике. Поэтому нашей дальнейшей целью будет вывести удобные правила для вычисления каждого из пяти типов определенного интеграла, следующие непосредственно из определения.
Пусть
![]() – непрерывная функция и
– непрерывная функция и![]() .
.
|
у
В
А
х О
Рис. 11
|
По определению определенного интеграла
разобьем
 на
на произвольных достаточно малых частей
произвольных достаточно малых частей ,
,выберем произвольные точки
 и вычислим
и вычислим ,
,найдем
 -ую
интегральную сумму
-ую
интегральную сумму .
Она численно равна площади ступенчатой
фигуры (рис. 11), ограниченной отрезком
.
Она численно равна площади ступенчатой
фигуры (рис. 11), ограниченной отрезком оси
оси ,
графиком функции и прямыми
,
графиком функции и прямыми и
и .
.очевидно, что
 численно равен площади криволинейной
трапеции
численно равен площади криволинейной
трапеции (рис.11), (если этот предел существует).
(рис.11), (если этот предел существует).
Геометрический
смысл определенного интеграла на
отрезке:
определенный интеграл от неотрицательной
на отрезке
![]() функции численно равен площади
криволинейной трапеции, ограниченной
графиком функции и отрезком
функции численно равен площади
криволинейной трапеции, ограниченной
графиком функции и отрезком![]() оси абсцисс.
оси абсцисс.
ЗАМЕЧАНИЕ.
Очевидно, что
 ,
то есть переменную интегрирования вопределенном
интеграле можно переобозначать: величина
интеграла от этого не зависит.
,
то есть переменную интегрирования вопределенном
интеграле можно переобозначать: величина
интеграла от этого не зависит.
ЗАМЕЧАНИЕ.
Если
![]() имеет на
имеет на![]() конечное число точек
конечное число точек
|
|
разрыва первого
рода (рис.12), то вычислить площадь,
ограниченную графиком функции и
отрезком
|
ОПРЕДЕЛЕНИЕ.
Функция
![]() называетсяинтегрируемой
на отрезке
называетсяинтегрируемой
на отрезке
![]() ,
если существует определенный интеграл
,
если существует определенный интеграл .
.
Таким образом, всякая кусочно-непрерывная на заданном отрезке функция интегрируема на этом отрезке.
ТЕОРЕМА
(о среднем значении). Пусть функция
![]() непрерывна
непрерывна![]() .
Тогда существует точка
.
Тогда существует точка![]() такая, что
такая, что
 (8.1)
(8.1)
ЗАМЕЧАНИЕ.
С геометрической точки зрения теорема
утверждает, что существует прямоугольник,
равновеликий криволинейной трапеции,
имеющий равное с ней основание (если
![]() ).
).
Значение
![]() называетсясредним
значением
функции на отрезке:
называетсясредним
значением
функции на отрезке:
 .
.
ДОКАЗАТЕЛЬСТВО.
Так как
![]() непрерывна
непрерывна![]() ,
то по второй теореме Вейерштрасса (см.
гл. 4)
,
то по второй теореме Вейерштрасса (см.
гл. 4)![]() достигает на
достигает на![]() своих наибольшего
своих наибольшего![]() и наименьшего
и наименьшего![]() значений:
значений:![]() всюду на отрезке.
всюду на отрезке.
Проинтегрируем
это неравенство на
![]() (свойство 5):
(свойство 5):
 .
.
Отсюда по свойствам 1, 2 определенного интеграла получим:

 ,
так как
,
так как
![]() .
.
|
|
По теореме о
промежуточных значениях (см. гл.4)
Что и требовалось доказать.
|
8.3. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница
Рассмотрим функцию
![]() .
Величина определённого интеграла от
этой функции
.
Величина определённого интеграла от
этой функции зависит от
зависит от![]() и
и![]() .
Если зафиксировать значение
.
Если зафиксировать значение![]() ,
то величина
,
то величина будет зависеть только от
будет зависеть только от![]() .
Зафиксируем нижний предел интегрирования
.
Зафиксируем нижний предел интегрирования![]() ,
а верхний будем считать переменным.
Чтобы подчеркнуть переменность верхнего
предела интегрирования, обозначим его
,
а верхний будем считать переменным.
Чтобы подчеркнуть переменность верхнего
предела интегрирования, обозначим его![]() .
Величина определённого интеграла, как
уже было отмечено, не зависит от
обозначения переменной интегрирования,
поэтому, чтобы не путать её с верхним
пределом, заменим переменную
.
Величина определённого интеграла, как
уже было отмечено, не зависит от
обозначения переменной интегрирования,
поэтому, чтобы не путать её с верхним
пределом, заменим переменную![]() внутри интеграла на
внутри интеграла на![]() .
.
Таким образом,
получим функцию
 .
Она называетсяопределённым
интегралом
с переменным
верхним пределом.
.
Она называетсяопределённым
интегралом
с переменным
верхним пределом.
ТЕОРЕМА
(о производной интеграла с переменным
верхним пределом). Пусть интегрируемая
на отрезке
![]() функция
функция![]() непрерывна в точке
непрерывна в точке![]() .
Тогда
.
Тогда .
.
ДОКАЗАТЕЛЬСТВО. По определению производной
 .
.

– здесь мы воспользовались свойством 3 аддитивности определенного интеграла. Отсюда по теореме о среднем значении
 ,
,
где
![]() – между
– между![]() и
и![]() .
Следовательно,
.
Следовательно, ,
так как
,
так как![]() ,
когда
,
когда![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
ЗАМЕЧАНИЕ.
Из теоремы следует, что
![]() – одна из первообразных функции
– одна из первообразных функции![]() на
на![]() ,
так как
,
так как![]() .
Значит, если
.
Значит, если![]() – другая первообразная, то
– другая первообразная, то![]() .
.
ТЕОРЕМА
(Ньютона–Лейбница).
Пусть функция
![]() непрерывна
непрерывна![]() и
и![]() – одна из её первообразных. Тогда
– одна из её первообразных. Тогда
 (8.2)
(8.2)
Формула (8.2) называется формулой Ньютона–Лейбница.
ДОКАЗАТЕЛЬСТВО.
Рассмотрим функцию
 .
По теореме о производной определённого
интеграла с переменным верхним пределом
она является первообразной для
.
По теореме о производной определённого
интеграла с переменным верхним пределом
она является первообразной для![]() на
на![]() .
Следовательно, если
.
Следовательно, если![]() – некоторая другая первообразная для
– некоторая другая первообразная для![]() ,
то
,
то![]()
![]() .
.
При
![]() ,
,
но
 .
.
При
![]() :
:![]() ,
,
откуда
 .
.
Переобозначив переменную интегрирования, получим требуемое:
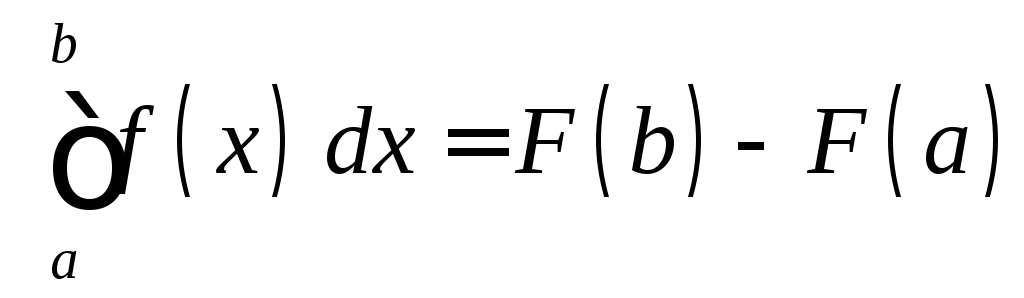 .
.
ЗАМЕЧАНИЕ.
Следует обратить внимание на важность
сформулированного в теореме требования
непрерывности функции
![]() на всем
отрезке интегрирования.
Небрежное применение формулы
Ньютона-Лейбница может привести к
заведомо неверному результату.
на всем
отрезке интегрирования.
Небрежное применение формулы
Ньютона-Лейбница может привести к
заведомо неверному результату.
ПРИМЕР.
Вычислить
![]() и
и![]() .
.
Если использовать
для вычисления первого интеграла формулу
Ньютона-Лейбница, то получается, что
 .
Но подынтегральная функция
.
Но подынтегральная функция![]() ,
поэтому полученный результат противоречит
свойству 4 определённого интеграла.
Причина этого в том, что функция
,
поэтому полученный результат противоречит
свойству 4 определённого интеграла.
Причина этого в том, что функция![]() имеет в точке
имеет в точке![]() разрыв второго рода (рис. 14), то есть не
является на отрезке
разрыв второго рода (рис. 14), то есть не
является на отрезке
|
|
|
ПРИМЕР.
Вычислить
 от функции, заданной на отрезке
от функции, заданной на отрезке![]()
|
|
двумя аналитическими выражениями:
Для вычисления такого интеграла надо воспользоваться свойством 3 аддитивности определенного интеграла:
|
 .
.
Замечание. Из формулы Ньютона-Лейбница следует, что
 ,
(8.3)
,
(8.3)
так как
![]() .
.































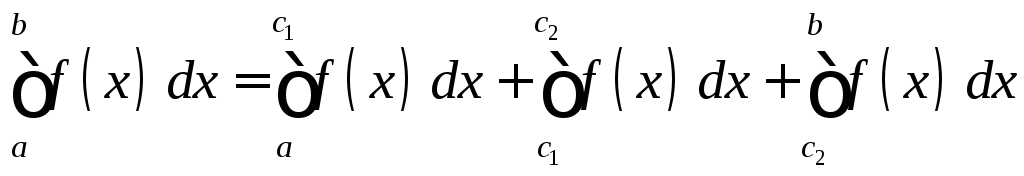 .
.
 .
Таким образом, существует, по крайней
мере, одна точка
.
Таким образом, существует, по крайней
мере, одна точка .
.
 .
.
 (рис. 15).
(рис. 15).