Глава 8. Определенный интеграл

8.1. Определенный интеграл по фигуре

Фигурой будем называть следующие геометрические объекты:

1) отрезок оси;

2) плоскую или пространственную кривую ;

3) плоскую область ;

4) пространственную поверхность ;

5) пространственную область .

Мерой отрезка и кривойбудем называть их длину, мерой областии поверхности– их площадь, мерой области– ее объем.

ОПРЕДЕЛЕНИЕ. Диаметром фигуры называется наибольшее расстояние между двумя ее точками.

ПРИМЕР. Диаметром отрезка является его длина , диаметром эллипса – длина его большой оси, диаметром куба – длина его диагонали.

Рассмотрим задачу о массе фигуры, плотность которой (линейная, поверхностная или объемная) переменна и задается непрерывной функцией: , гдеР – произвольная точка фигуры.

1) Пусть имеется неоднородный стержень длины , линейная плотность которого задана непрерывной функцией. Найдем массу этого стержня.

Если бы стержень был однородным, то есть его линейная плотность , то масса вычислялась бы по хорошо известной формуле:. Свести решение поставленной задачи об определении массы неоднородного стержня к использованию этой формулы можно таким образом:

1. Разобьем отрезок напроизвольных достаточно малых частей точками (рис.7).

2. Так как функция непрерывна, то в пределах малого отрезка еёизменение незначительно, следовательно, можно считать, что . Поэтому выберем на каждом отрезкепроизвольную точку (рис.7) и будем считать, что.

3. Вычислим приближенное значение массы каждого малого отрезка: .

4. Масса всего стержня 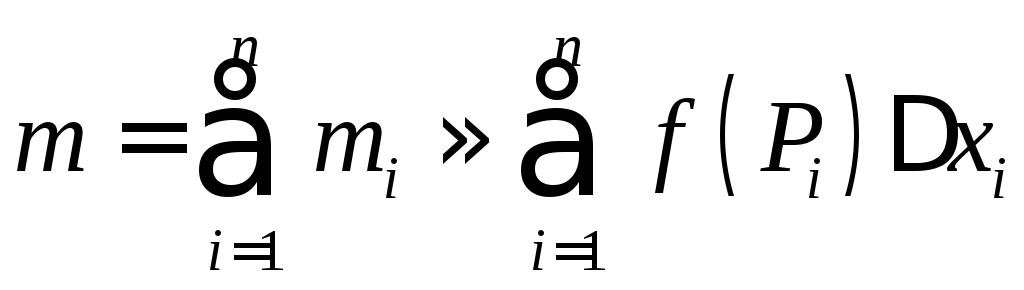, причем это приближенное равенство, очевидно, тем точнее, чем больше количество отрезков и меньше длина каждого из них. Значит, естественно считать, что, если этот предел существует и не зависит от способа разбиенияна малые части и выбора точек;– наибольший из диаметров отрезков.

2) Если надо найти массу криволинейного стержня ,то аналогично разобьем его на достаточно малых произвольных частей (рис.8), выберем в

каждой части произвольную точку , тогда , где – наибольший из диаметров частей,

3) Для плоской пластинки (рис.9),

где – наибольший из диаметров частей,

4) Для пространственной пластинки (рис.10),

где – наибольший из диаметров частей,

5) Массу пространственного тела можно найти аналогично: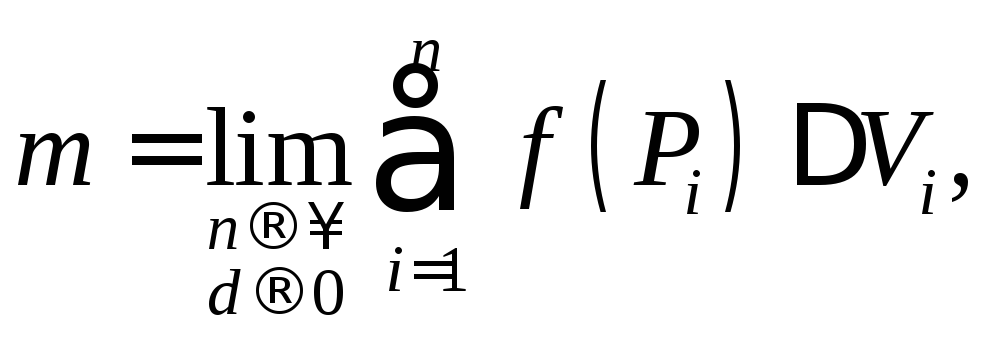где– наибольший из диаметров частей.

Отвлекаясь от физического содержания задачи, проанализируем математические действия, выполняемые при ее решении.

Пусть во всех точках фигуры задана непрерывная функция .

1. Разобьем фигуру на произвольных достаточно малых частей.

2. Выберем в каждой малой части произвольную точку и считаем, что вследствие непрерывности функциив пределахi-ой части ,.

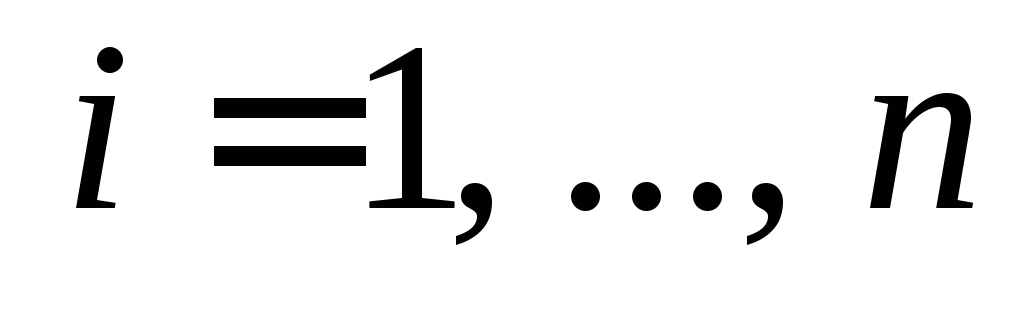3. Умножим 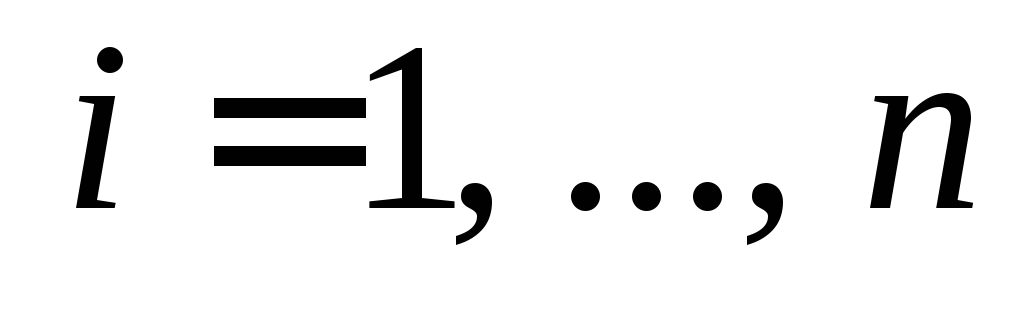на меру соответствующей малой части.

4. Составим сумму полученных произведений, которую назовем –ойинтегральной суммой :

для ;

для кривой ;

для плоской области ;

для пространственной поверхности ;

для пространственного тела .

Если существует предел интегральной суммы , когда число частей разбиения неограниченно растет, а размеры наибольшей из них стягиваются в точку, причем этот предел не зависит от способа составления интегральной суммы, то он называетсяопределенным интегралом по фигуре от функции .

ОПРЕДЕЛЕНИЕ. Определенным интегралом по фигуре от заданной на ней непрерывной функции называется предел -ой интегральной суммы, когда стремится к бесконечности число частей, на которые разбивается фигура при её составлении, а наибольший из диаметров этих частей стремится к нулю. Причем этот предел существует и не зависит от способа составления интегральной суммы.

Итак, соответствующие интегралы обозначаются и называются следующим образом:

–определенный интеграл на отрезке;

–криволинейный интеграл 1 рода (по длине дуги);

–двойной интеграл;

–поверхностный интеграл 1 рода (по площади поверхности);

–тройной интеграл.

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПО ФИГУРЕ

Пусть во всех точках фигуры заданы непрерывные функциии. Непосредственно из определения следуют следующие свойства определенного интеграла:

1. Если , то определенный интеграл по фигуре равен мере соответствующей фигуры:

.

2. – свойстволинейности определенного интеграла.

3. Если фигура F разбита на конечное число частей , то– свойствоаддитивности определенного интеграла.

4. Если во всех точках фигуры , то.

5. Если во всех точках фигуры, то.

6. Среднее интегральное значение функции на фигуревычисляется по формуле

,

где – мера фигуры.