7.6. Интегрирование некоторых тригонометрических функций

Рассмотрим некоторые часто встречающиеся приемы нахождения неопределенных интегралов от тригонометрических функций.

1. Интегралы вида , где одно из чиселилинечетно и положительно, а другое – произвольное действительное число.

Если ,, то, поэтому подынтегральное выражение в этом случае можно переписать в виде:

Аналогично, если ,, то подынтегральное выражение будет зависеть только от.

ПРИМЕР. Найти .

.

2. Интегралы вида где.

В этом случае надо понизить степень подынтегральной функции по одной из тригонометрических формул понижения степени:

.

ПРИМЕР. Найти .

Так как , то, поэтому

.

3. Интегралы вида где.

В этом случае надо, последовательно отделяя от подынтегральной функции множитель или, заменять его, используя одну из тригонометрических формул:

.

ПРИМЕР. Найти .

Очевидно, , поэтому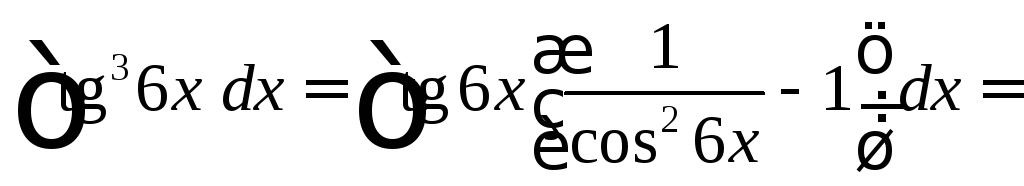

.

ПРИМЕР. Найти .

.

4. Интегралы вида , где– рациональная функция, зависящая от

Если при интегрировании тригонометрического выражения, не содержащего радикалов, не удалось применить ни один из приемов из пунктов 1–3, то подстановка , которая называетсяуниверсальной тригонометрической подстановкой, сведет этот интеграл к интегралу от рациональной дроби. При этом надо использовать тригонометрические формулы:

.

ПРИМЕР. Найти .

Сделаем универсальную подстановку:

.

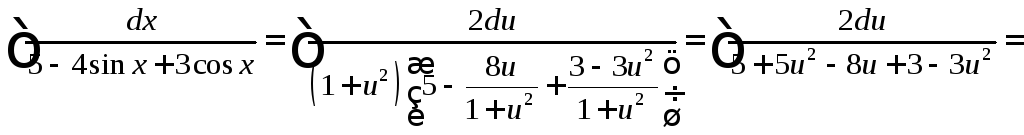
5. Интегралы вида , где– рациональная функция, в которуювходят только в четных степенях.

Для интегралов такого вида возможно применение универсальной тригонометрической подстановки, однако после нее подынтегральной выражение может получиться очень громоздким. Поэтому в таких случаях следует сделать замену переменных по формуле и использовать тригонометрические формулы:.

ПРИМЕР. Найти .

Делаем замену переменных:

.

.

7.7. Интегрирование некоторых иррациональных выражений

Рассмотрим некоторые приемы вычисления интегралов от иррациональных выражений, то есть выражений, содержащих радикалы.

1. Интегралы вида , где– рациональная функция своих аргументов. Это означает, что подынтегральная функция содержит корни только степенейи никаких других.

В этом случае подынтегральное выражение станет рациональным после введения новой переменной по формуле , где– наименьшее общее кратное чисел.

ПРИМЕР. Найти .

.

.

2. Интегралы вида , где– рациональная функция своих аргументов, что означает, что она содержит только квадратные корни.

Если подкоренное выражение – квадратный трехчлен, то кажущаяся в данном случае естественной замена почти никогда не позволяет избавиться от иррациональности.

ПРИМЕР. Найти .

Пусть .

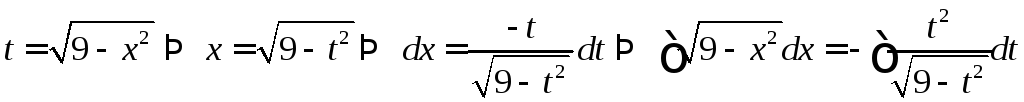Таким образом, в результате такой замены подынтегральное выражение осталось иррациональным.

Гарантировано избавляют от иррациональности в интегралах такого вида тригонометрические подстановки или.

Если , тоВ другом случае.

3. Интегралы вида .

В этом случае выражение рационализируется подстановками или.

Если , то. Аналогичные формулы получаются и для замены вида.

4. Интегралы вида .

Для интегралов такого вида следует ввести новую переменную по формуле:

.

Тогда

.

Кроме этого, можно положить .

ПРИМЕР. Найти а) , б).

а) Очевидно, этот интеграл имеет вид, представленный в пункте 4, поэтому введем новую переменную по формуле

,

так как из формулы замены переменной следует, что .

б) Этот интеграл соответствует пункту 2, поэтому сделаем такую подстановку:

,

так как из формулы замены переменной следует, что .