
- •Н.И. Николаева интегральное исчисление
- •Часть 4
- •Оглавление
- •Глава 7. Неопределенный интеграл
- •7.1. Определение и свойства неопределенного интеграла
- •7.2. Основные формулы и методы интегрирования.
- •7.3. Замена переменной в неопределенном интеграле
- •7.4. Интегрирование по частям
- •7.5. Интегрирование рациональных дробей
- •7.6. Интегрирование некоторых тригонометрических функций
- •7.7. Интегрирование некоторых иррациональных выражений
- •Глава 8. Определенный интеграл
- •8.1. Определенный интеграл по фигуре
- •8.2. Определенный интеграл на отрезке
- •8.3. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница
- •8.4. Интегрирование по частям в определенном интеграле
- •8.5. Замена переменной в определенном интеграле
- •8.6. Геометрические приложения определенного интеграла на отрезке
- •8.7. Несобственные интегралы. Интегралы с бесконечными пределами интегрирования
- •8.8. Исследование сходимости несобственных интегралов с помощью признаков сравнения
- •8.9. Интегралы от неограниченных функций
7.5. Интегрирование рациональных дробей
ОПРЕДЕЛЕНИЕ.
Дробно-рациональной
функцией (рациональной дробью)
называется функция вида
 ,
,
где
![]() – многочлен степени
– многочлен степени![]() ,
,
![]() –многочлен степени
–многочлен степени
![]() .
.
ОПРЕДЕЛЕНИЕ.
Рациональная дробь называется правильной,
если
![]() ;
если
;
если![]() – тонеправильной.
– тонеправильной.
ПРИМЕРЫ.
![]() – неправильная рациональная дробь:
– неправильная рациональная дробь:![]() ;
;
![]() –правильная
рациональная дробь:
–правильная
рациональная дробь:
![]() ;
;
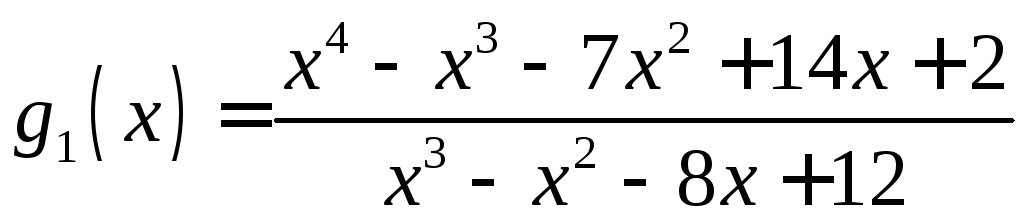 –неправильная
рациональная дробь:
–неправильная
рациональная дробь:
![]() ;
;
 –правильная
дробь:
–правильная
дробь:
![]() .
.
Процесс интегрирования рациональных дробей состоит из нескольких этапов и опирается на некоторые факты из высшей алгебры, которые мы примем без доказательства.
УТВЕРЖДЕНИЕ 1. У всякой неправильной рациональной дроби можно выделить целую часть, то есть представить ее в виде многочлена и правильной рациональной дроби.
ПРИМЕР.
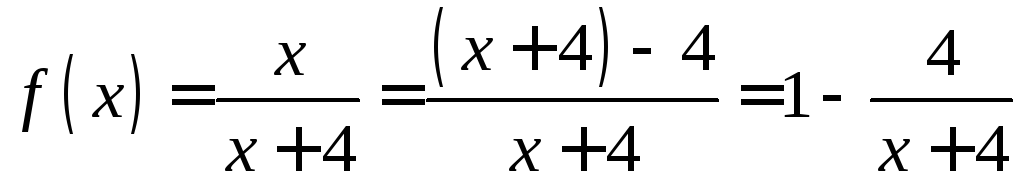 :
:
![]() 1–
целая часть этой рациональной дроби
(многочлен нулевой степени),
1–
целая часть этой рациональной дроби
(многочлен нулевой степени),
![]() –правильная
дробь.
–правильная
дробь.
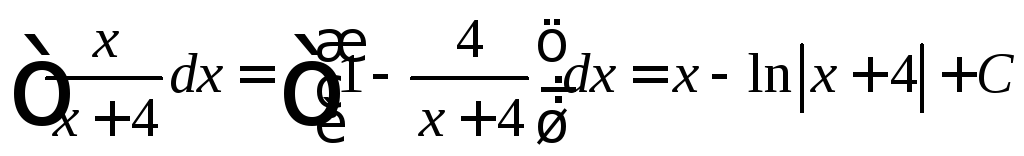 .
.
ПРИМЕР.
Чтобы выделить целую часть из неправильной
дроби
 ,
надо числитель разделить на знаменатель,
используя алгоритм деления «уголком»
с остатком:
,
надо числитель разделить на знаменатель,
используя алгоритм деления «уголком»
с остатком:
 .
.
В этом случае
![]() – целая часть (многочлен первой степени),
– целая часть (многочлен первой степени),![]() – остаток от деления, поэтому
– остаток от деления, поэтому
 .
.
Таким образом, задача интегрирования рациональной дроби сводится к задаче интегрирования многочлена и правильной рациональной дроби.
УТВЕРЖДЕНИЕ 2. Для того, чтобы найти интеграл от правильной рациональной дроби, надо разложить ее знаменатель на множители. Всякий многочлен можно представить в виде произведения линейных множителей и квадратных трехчленов с отрицательным дискриминантом
![]() .
.
Если в разложении
многочлена на множители есть линейный
множитель
![]() ,
то число
,
то число![]() называетсякорнем
многочлена.
называетсякорнем
многочлена.
ПРИМЕР.
Разложить на множители
![]() .
.
Старший коэффициент
этого многочлена – при
![]() – равен единице. Такие многочлены
называютсяприведенными.
Чтобы разложить его на множители,
необходимо найти хотя бы один его корень.
Для этого воспользуемся следующим
фактом.
– равен единице. Такие многочлены
называютсяприведенными.
Чтобы разложить его на множители,
необходимо найти хотя бы один его корень.
Для этого воспользуемся следующим
фактом.
ТЕОРЕМА (Безу). Если приведенный многочлен с целыми коэффициентами имеет целые корни, то они являются делителями его свободного члена.
Свободный член
многочлена
![]()
![]() .
Делителями числа 12 являются
.
Делителями числа 12 являются![]() .
Проверяя поочерёдно эти числа, убеждаемся,
что 1 и –1 не являются корнями
.
Проверяя поочерёдно эти числа, убеждаемся,
что 1 и –1 не являются корнями![]() ,
а
,
а![]() – корень:
– корень:![]() .
Это значит, что в разложении
.
Это значит, что в разложении![]() на множители есть линейный множитель
на множители есть линейный множитель![]() .
Разделим
.
Разделим![]() на
на![]() «уголком» (без остатка):
«уголком» (без остатка):
 .
.
Отсюда
![]() .
Это означает, что многочлен
.
Это означает, что многочлен![]() имеет три действительных корня:
имеет три действительных корня:![]() и
и![]() .
Корень
.
Корень![]() называетсяпростым
корнем: в полученном разложении ему
соответствует линейный множитель
называетсяпростым
корнем: в полученном разложении ему
соответствует линейный множитель
![]() .
Значение
.
Значение![]() называется корнем кратности 2 (кратным
корнем), так как в разложении
называется корнем кратности 2 (кратным
корнем), так как в разложении
![]() на множители ему соответствует множитель
второй степени
на множители ему соответствует множитель
второй степени![]() .
.
Таким образом,
 .
.
ОПРЕДЕЛЕНИЕ. Простейшими рациональными дробями называются дроби вида
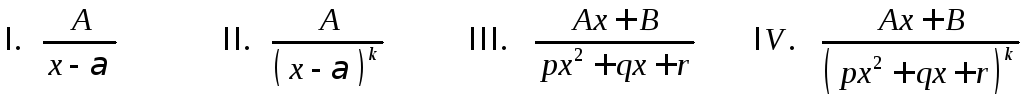 ,
,
где
![]() .
.
УТВЕРЖДЕНИЕ 3.
Всякая правильная
рациональная
дробь может быть разложена в сумму
простейших.
При этом если в разложении знаменателя
есть множитель
![]() ,
то ему соответствует
,
то ему соответствует![]() слагаемых в разложении дроби в сумму
простейших: одно слагаемое типа
слагаемых в разложении дроби в сумму
простейших: одно слагаемое типа![]() и
и![]() слагаемое типа
слагаемое типа![]() ;
множителю
;
множителю![]() соответствует слагаемое типа
соответствует слагаемое типа![]() ;
множителю
;
множителю![]() соответствует одно слагаемое типа
соответствует одно слагаемое типа![]() и
и![]() слагаемое типа
слагаемое типа![]() .
.
Таким образом, число слагаемых, соответствующих каждому сомножителю знаменателя, в разложении правильной дроби в сумму простейших равно степени, в которой этот сомножитель входит в разложение знаменателя на множители.
Следовательно,
задача
интегрирования правильной рациональной
дроби сводится к задаче разложения ее
в сумму простейших и интегрированию
дробей вида
![]() .
.
При определении коэффициентов разложения правильной дроби в сумму простейших применяется метод неопределенных коэффициентов.
Поясним сказанное на примерах.
ПРИМЕР. Написать вид разложения в сумму простейших следующих правильных дробей
а)
 ; б)
; б) ;
;
в)
 .
.
а) Знаменатель
дроби
![]() содержит четыре множителя, поэтому
содержит четыре множителя, поэтому ,
то есть сумма состоит из четырех
слагаемых: по одномуI
и III
типов и два слагаемых II
типа.
,
то есть сумма состоит из четырех
слагаемых: по одномуI
и III
типов и два слагаемых II
типа.
б) Квадратный
трехчлен
![]() имеет отрицательный дискриминант,
поэтому в разложении в сумму простейших
дроби
имеет отрицательный дискриминант,
поэтому в разложении в сумму простейших
дроби![]() будут слагаемыеI,
III,
IV
типов:
будут слагаемыеI,
III,
IV
типов:
 .
.
в) В знаменателе
дроби
![]() – шесть сомножителей, следовательно,
– шесть сомножителей, следовательно,
 .
.
Неопределенные коэффициенты А, В, С, … в написанных равенствах должны быть найдены так, чтобы эти равенства выполнялись тождественно.
ПРИМЕР. Разложить в сумму простейших правильную дробь
 .
.
Представим эту
дробь в виде суммы:
 ,
где
,
где![]() – не определенные пока коэффициенты,
и теперь задача состоит в том, чтобы
найти их.
– не определенные пока коэффициенты,
и теперь задача состоит в том, чтобы
найти их.
Приведя сумму, стоящую справа, к общему знаменателю, приравняем числители дробей в обеих частях равенства:
![]() .
.
Далее можно действовать двумя способами.
Способ 1.
Это равенство является тождеством, то
есть справедливо при всех значениях
![]() .
.
Пусть
![]() ,
тогда, подставив это значение в правую
и левую часть, получим:
,
тогда, подставив это значение в правую
и левую часть, получим:![]() .
.
При
![]() ;
при
;
при![]() .
.
Заметим, что
![]() – действительные корни знаменателя
рассматриваемой дроби. При этих значенияхx
соответствующие неопределенные
коэффициенты нашлись совсем просто.
Так как отличных от этих корней знаменатель
не имеет, то для определения коэффициента
А
можно было взять любое другое (вместо
– действительные корни знаменателя
рассматриваемой дроби. При этих значенияхx
соответствующие неопределенные
коэффициенты нашлись совсем просто.
Так как отличных от этих корней знаменатель
не имеет, то для определения коэффициента
А
можно было взять любое другое (вместо
![]() )
значение. Например, при
)
значение. Например, при![]() :
:
![]() .
.
Способ 2.
Так как это равенство является тождеством,
то коэффициенты при одинаковых степенях
![]() слева и справа равны. Поэтому раскроем
скобки в правой части равенства и
приравняем коэффициенты при одинаковых
степенях
слева и справа равны. Поэтому раскроем
скобки в правой части равенства и
приравняем коэффициенты при одинаковых
степенях![]() :
:
![]()

Решая полученную
систему линейных уравнений, найдем
неизвестные коэффициенты
![]() .
.
Анализируя оба способа нахождения неопределенных коэффициентов, можно сделать следующий вывод:
способ 1 надо применять, когда все корни знаменателя действительны и различны; если это не так, то способ 1 следует применить для нахождения тех коэффициентов, где это удобно, а для нахождения оставшихся применить способ 2, написав уже не все уравнения, а лишь столько, сколько необходимо для определения ненайденных коэффициентов.
В рассмотренном
примере легко находятся
![]() и
и![]() :
:
![]() .
.
Так как осталось
определить лишь
![]() ,
составим еще одно уравнение, приравняв
коэффициенты, например, при
,
составим еще одно уравнение, приравняв
коэффициенты, например, при![]() справа и слева:
справа и слева:![]() .
.
Итак, теперь все
готово для того, чтобы найти первообразную
рациональной дроби
![]() .
.
ПРИМЕР.
Найти
 .
.

 .
.
ВЫВОД. Для того чтобы проинтегрировать рациональную дробь, надо
выделить целую часть, если дробь неправильная;
разложить знаменатель на линейные множители и квадратные трехчлены с отрицательным дискриминантом;
разложить правильную рациональную дробь в сумму простейших;
проинтегрировать многочлен и простейшие дроби.
