7.3. Замена переменной в неопределенном интеграле

Пусть требуется найти неопределенный интеграл , но непосредственно подобрать первообразную дляне удается, хотя известно, что она существует. Во многих случаях введением вместо переменной интегрированиянекоторой новой переменной можно данный интеграл свести к другому, который или содержится в таблице основных интегралов или легко вычисляется другим способом.

Такой метод называется методом замены переменной, или методом подстановки.

Итак, введем новую переменную по формуле – дифференцируемая функция на некотором интервале, при этом функциянепрерывна на соответствующем интервале изменения. Тогда

, (7.1)

(7.1) – формула замены переменной в неопределенном интеграле.

ПРИМЕР. Найти .

Сделаем замену переменной по формуле:

.

Для вычисления удобно использовать определение тригонометрических функций в прямоугольном треугольнике:– отношение противолежащего катетак прилежащему 1,– отношение противолежащего катетак гипотенузе(рис.1).

ПРИМЕР. Найти .

Пусть

.

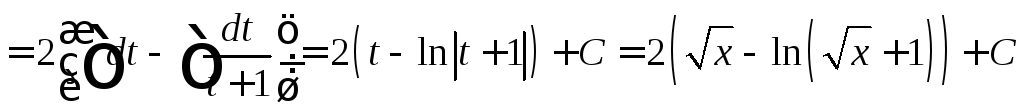7.4. Интегрирование по частям

Пусть – дифференцируемые функции, тогда дифференциал их произведения. Интегрируя это равенство, получим (свойства 2,3):

(7.2)

Формула (7.2) называется формулой интегрирования по частям.

Эта формула применяется к интегрированию выражений, которые можно представить в виде произведения двух сомножителей итак, что отыскание функциипо ее дифференциалуи вычисление интеграласоставляет в совокупности задачу более простую, чем непосредственное вычисление.

Рассмотрим некоторые часто встречающиеся интегралы, которые находятся по формуле (7.2).

1. Интегралы вида – многочлен-ой степени.

Эти интегралы берутся по частям, если положить .

ПРИМЕР. Найти .

Пусть тогда все остальное в подынтегральном выражении –:. Найдем. Применяя формулу (7.2), получим:

.

Если подынтегральное выражение в интегралах такого типа содержит многочлен -ой степени, то формулу интегрирования по частям следует применитьраз.

ПРИМЕР. Найти .

2. Интегралы вида – многочлен-ой степени. Во всех этих случаях– функция, являющаяся множителем при,.

ПРИМЕР. Найти .

.

ПРИМЕР. Найти .

.

ЗАМЕЧАНИЕ. Не всякий интеграл, содержащий обратную тригонометрическую функцию или логарифм, находится методом интегрирования по частям.

ПРИМЕР. Найти .

По определению дифференциала , поэтому

.

ПРИМЕР. Найти .

Заметим, что , поэтому.

3. Циклические, или возвратные интегралы .

После двукратного интегрирования по частям получается выражение, содержащее исходный интеграл. Рассматривая его, как уравнение относительно неизвестного интеграла, находят искомую первообразную. В этом случае не имеет принципиального значения, какой из сомножителей обозначить . Важно лишь, чтоб оба раза это была или показательная или тригонометрическая функция.

ПРИМЕР. Найти .

.

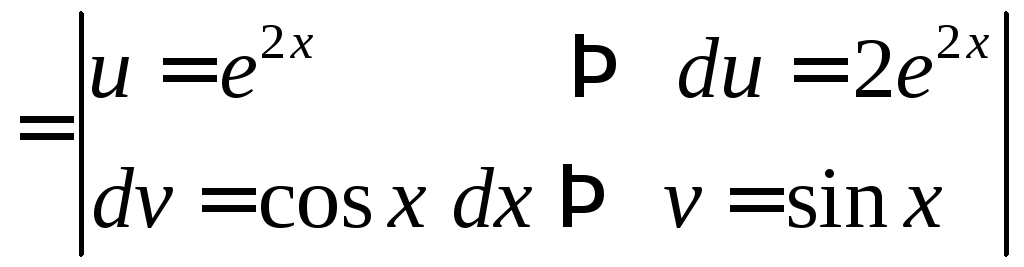
После повторного интегрирования по частям мы пришли к исходному интегралу. Раскрывая скобки и приводя подобные, получим:

.

Отсюда следует, что .

ЗАМЕЧАНИЕ. В пунктах 1–3 описаны наиболее типичные и часто встречающиеся интегралы, которые находятся методом интегрирования по частям. Но формула (7.2) может применяться и для вычисления других интегралов.

ПРИМЕР. Найти

.

Полученный результат можно рассматривать как уравнение относительно неизвестного интеграла Перенесем его в правую часть, разделим обе части равенства на 2 и получим:

.